关于复射影空间中若干子流形问题的研究

韩拥军

(铜陵职业技术学院，安徽 铜陵 244000)

关于复射影空间中若干子流形问题的研究

韩拥军

(铜陵职业技术学院，安徽 铜陵 244000)

文章从系统层面整体分析了复射影空间中的各种子流形，对其进行简单分类和典型分析，研究了子流形的曲率与几何的数学关系，掌握了复射影空间中若干子流形的基本特质，证明了所推理的若干积分公式的正确性。

复射影空间；CR子流形；一般子流形；全脐子流形

一、全实全脐和全实伪脐子流形定理研究

1.准备

多维度的向量空间，假设为n维，定义 Cn，列举多个（n）复数以一定序列排列成为数组，构建复向量空间。将其中各种元素标记为Z,集合设定为Z=(Z1，…Zn)。

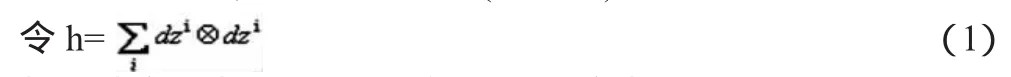
故可认定h为Cn上的K度量，取其实为

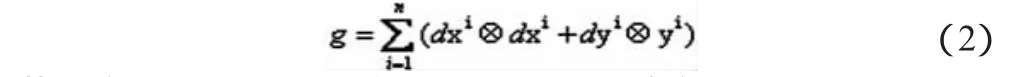
2.定理

假定CPi+j是i+j维的复射影空间，全纯截曲率为3，其实维子流形上的一点的切向空间如果被变换到自身的话，那么就可以将CPi+j定义为是全纯子流形；但是，如果其实维子流形上的一点的切向空间没有变换到其自身上，而是在该点的一个垂直空间上，那样的话CPi+j的定义就为全实子流形。上述两种定义的不变子流形是CPi+j唯一具有的，也可以理解为CPi+j的变化对于其中的任何一点的切向的空间的曲率是不会产生影响的。

对于CPi+j的全实子流形

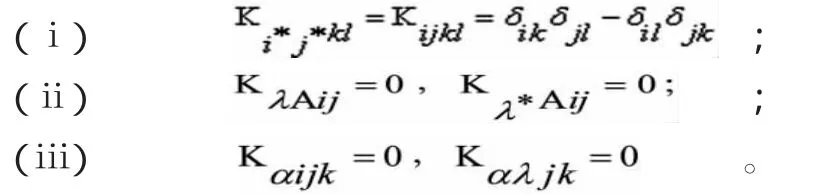
3.基本公式

CPi+j基本公式：

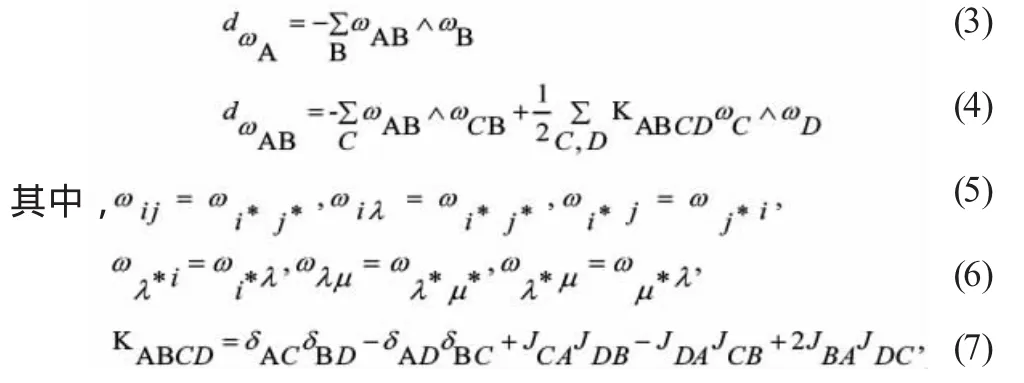
4.定理证明

二、具有平坦法丛的一般极小子流形

1.基本概念

假定M是一个具有近复结构的复流形。子流形N作为以相等距离浸入于复流形M。如果在N的浸入子流形上，取属于它的任何一点的切向空间，如果按照近复结构的变换方式使得在这个点的垂直空间内能够找到它的切向空间，那么我们称N是属于M的一个全实子流形或全纯子流形；如果N上任意一点的变换方式正好与前者相反，那么我们称N是M的一般性的子流形。一个特殊的情况就是，如果当且仅当满足codimN=1时，那么N被称为是属于M的实超曲面。

2.定理

（ⅰ）具有全测的、平坦法丛的一般极小子流形在复射影空间中是不存在的；

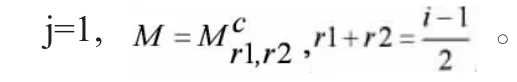
三、CR-子流形

接下来我们就开始证明，

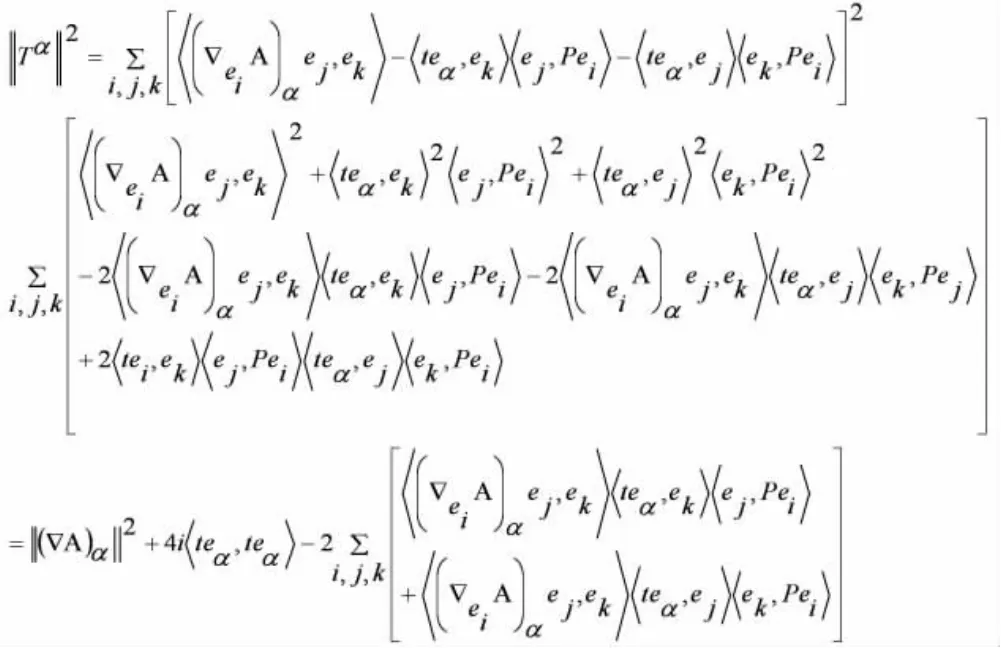
接下来再对上式中最右端中括号中的项进行计算，

由上式的计算结果，我们可以得到以下结论：

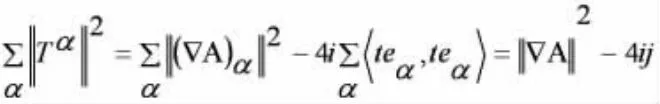
由此定理（ⅱ）的证明就完成了。

4.基本公式

（ⅰ）假设CPm的CR-流形是M2i+j，且M2i+j是无边界紧致的可以定向的连通流形。对于一个光滑的映射f：M2i+j→R作为一个次调和函数应用在M2i+j流形上，也就是能够满足不等式，由此可得，函数f是一个常值函数。即表示为：

同理，假设CPm的CR-极小子流形是M2i+j，且M2i+j是无边界紧致的可以定向的连通流形。对于一个光滑的映射f： M2i+j→R作为一个次调和函数应用在M2i+j流形上，也就是能够满足不等式，由此也可得到函数f是一常值函数。即表示为：

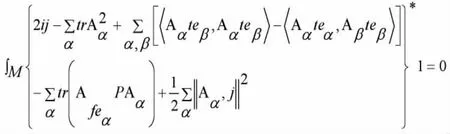
在这里我们要考虑的一种特殊情况就是，对于一般CR-极小子流形M2i+j，能够满足的是：

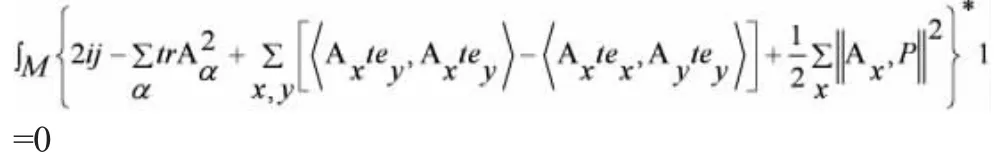
（ⅱ）假设CPm的CR-流形是M2i+j，且M2i+j是无边界紧致的可以定向的平坦法丛的连通流形。那么，

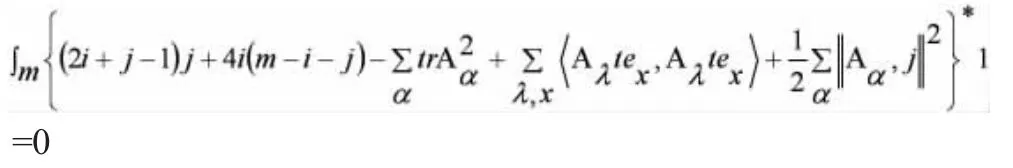
[1]Chen B Y，Ogiue K.On totally real submanifolds[J].Trans AMS，1974,193:257-266.

[2]徐林林，薛春华.微分几何[M].合肥：中国科学技术大学出版社，1997.

[3]Chern S S,do Carmo M,Kobayashi S,Minimal submanifolds of a sphere with second fundamental form of constant length,Functional Analysis and Related Fields[M].Spring-Verlage,1970,59-75.

[4]Yano K,Kon M.Generic submanifolds[J].Ann.Mat.Pura. Appl,1980,123:59-92.

[5]Bejancu A,Kon M,Yano K.CR-submanifolds of a complex space form[J].J.Diff.Geom.,1981,16:137-145.

[6]Tashiro Y,Tachibanna S.On Fubinian and C-Fubinian manfolds[J].Kodai Math.Sem.Rep.,1963,15:176-183.

[7]沈一兵.关于复射影空间中的一般极小子流形[J].数学进展，1986,15（2）：205-210.

[8]东瑜昕.复射影空间中的CR-子流形[J].数学学报，1993,36（3）：321-334.

[9]Kon M.Real minimal hypersurface in a complex projective space[J].Proc.A.M.S.,1980,79:285-288.

（责任编辑：刘忠义）

O174

A

1671-752X（2012）02-0067-03

2012-04-26

韩拥军（1968-），女，安徽铜陵人，铜陵职业技术学院信息工程系讲师，硕士，研究方向：泛函微分方程。

2012年安徽省教育厅一般项目（编号：KJ2012B197）研究成果。