弹性地基上具有轴向载荷的充液周期管弯曲振动带隙研究

迟乾坤，温激鸿，郁殿龙

(1.国防科学技术大学 机电工程研究所，长沙 410073;2.国防科学技术大学 装备综合保障技术重点实验室，长沙 410073)

输液管道在石油、化工、机械、航空等领域应用比较广泛，近代以来人们对于输液管道振动进行了大量的研究，其研究方法和研究成果极为丰富［1］。输液管道一般置于具有一定弹性参数的地基之上，对弹性地基上的管道振动进行研究，对实现管道减振降噪具有十分重要的工程意义。为方便研究，引入了不同的地基模型，例如单参数模型［2］和双参数模型［3］，这些都极大地方便了对输液管道振动的分析，也成为了振动控制领域的研究热点。

研究发现当弹性波在周期性结构中传播时，会产生带隙特性，即特定频率范围内的弹性波传播受到抑制。这种具有弹性波带隙的周期性复合材料或结构人们称之为声子晶体［4］，声子晶体的带隙特性在减振降噪方面具有广阔的应用前景。

Koo［5］研究周期弹性支撑的管路，发现了弯曲振动带隙，并进行了实验验证。郁殿龙等［6－7］利用声子晶体思想对周期管路进行了研究，并对轴向载荷作用下的周期结构梁弯曲振动带隙进行了分析。但是轴向载荷和弹性地基共同作用在充液管路上的研究尚未得到开展。

本文基于 Winkle地基模型［2］和 Euler-Bernoulli梁理论［8］，利用传递矩阵法对单参数弹性地基上具有轴向载荷的充液周期管路弯曲振动进行研究，并分析弹性地基和轴向载荷对弯曲振动带隙的影响规律。

1 研究模型

图1为弹性地基上的充液周期管路结构示意图，管路A和管路B沿着x轴交替排列形成周期结构，管路A和管路B可以有不同的材料参数，也可以有不同的几何参数，本文以材料周期管路为研究对象。图1(a)为无限周期结构示意图，图1(b)为周期管路的横截面，其内外半径分别为ri和ro，图1(c)为单个周期结构示意图，设管路A和管路B的长度分别为a1和a2，则单个周期管路长度即晶格常数a=a1+a2。

图1 弹性地基上充液周期管路结构示意图Fig.1 Schematic diagram of periodic pipe conveying fluid on elastic foundation

对于管路的弯曲振动，不考虑Poisson耦合的影响，假设液体中没有空泡现象，同时忽略液体与管壁内部摩擦、重力、外部压力以及温度变化的影响，此时管路弯曲振动方程为［9］:

其中:w为y方向振动位移，E为杨氏模量;I为管路的截面转动惯量;mf和mp分别为单位长度流体和管路质量，u为流体平均速度，t为时间，T为轴向载荷。R为弹性地基的反作用力［3］:

其中:kf为地基刚度系数。

式(1)的解可写成 w(x，t)=Wekxeiωt的形式，代入式(1)可得:

对于给定的ω，式(3)包括四个不同的根，分别设为 k1，k2，k3，k4。则式(1)的解为:

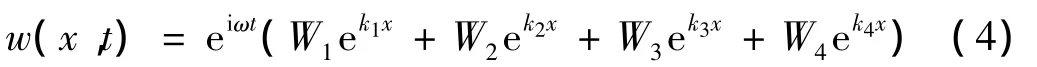
对于周期管路系统，其界面处的位移w，斜率w'，弯矩EIw″以及剪切力EIw‴都是连续的。根据传递矩阵方法以及Bloch理论［4］，可以得到标准的矩阵特征值方程为:

其中:I为4×4单元矩阵，M为传递矩阵。通过求解矩阵M的特征值，即可得到波矢q与频率ω之间的色散关系，进而得到无限周期充液管路的能带结构。

2 弹性基地上弯曲波的传播特性

为便于分析一维充液管路弯曲振动的传播特性，计算了弹性地基上均匀材料管弯曲波的波数。管路内半径 ri=0.045 m，外半径 ro=0.05 m，地基参数 kf=1×105Pa。管路材料选择为铝，密度 ρAL=2 730 kg/m3，杨氏模量 EAL=7.756×1010Pa。液体水的密度ρw=1 000 kg/m3，流体速度为10 m/s。图2为弹性地基上铝管弯曲波波数和频率的关系曲线。图2(a)和图2(b)分别为k1的实部和虚部，图2(c)和图2(d)分别为k2的实部和虚部，图2(e)和图2(f)分别为k3的实部和虚部，图2(g)和图2(h)分别为k4的实部和虚部。

依据方程(3)图2中的拐点可以通过下式给出:

通过上式可以发现，该频率点仅与管路线密度和地基刚度系数有关，与管路的振动状态无关。分析可知当f＜f0时，k1和k2都有实部和虚部，在其他频率范围内，它们只有虚部。表明当f＜f0时弯曲波ek1x和ek2x为衰减波，当f＞f0时为行波。对于k3和k4，在整个频率范围内都有实部，表明弯曲波ek3x和ek4x为近场衰减波。

图2 弹性地基上铝管弯曲波波数Fig.2 Wavenumbers of the flexural wave in aluminium pipe on elastic foundation

3 弹性地基对带隙的影响

在图1所示的周期管路中，取管路A的材料为铝，管路B为环氧树脂。计算用参数管路内外半径分别为ri=0.045 m，ro=0.05 m。铝密度 ρA=2 730 kg/m3，杨氏模量EA=7.756×1010Pa;环氧树脂密度ρB=1 180 kg/m3，杨氏模量EB=4.35×109Pa。液体水的密度 ρw=1 000 kg/m3，流体速度为10 m/s。取周期管路的晶格常数a=1 m，其中a1=a2=0.5 m。

首先计算了没有弹性地基时周期管路和铝质均匀管路的能带结构，即kf=0 Pa时。图3为无弹性地基时周期管路和铝质均匀管路弯曲振动能带结构，可发现铝质均匀管不存在弯曲振动带隙，周期管路在0～1 000 Hz的频率范围内，存在三个布拉格带隙，分别为50.6 ～89.6 Hz，243 ～401.9 Hz，667 ～822.2 Hz。

图4给出了当kf=1×105Pa时周期管路和铝质均匀管路弯曲振动能带结构，同样铝质均匀管路不存在弯曲振动带隙，周期管路的前三个带隙频率范围分别为 53.5 ～90.8 Hz，244 ～402.7 Hz，668 ～822.4 Hz。与图3中的带隙相比较，可发现弹性地基作用使得周期管路的带隙频率升高。

图4中在0～16.6 Hz之间，能带结构不存在色散曲线，这是因为当 f＜f0时，弯曲波的传递始终是衰减的。由于关键频率点仅与管路线密度和地基刚度系数有关，因而可将周期管路的线密度进行等效处理，进而通过方程(6)计算出周期管路的关键频率。此时方程(6)中周期管路的等效线密度SA和SB分别为铝管和环氧树脂管的横截面积。等效后由方程(6)得到的周期管路关键频率值为16.5 Hz，而图4中色散曲线中的关键频率值为16.6 Hz，两者相吻合，说明对于周期管路的关键频率，利用等效密度通过方程(6)计算是合理的。

4 轴向载荷对带隙的影响

轴向载荷在管路系统中是普遍存在的，其对管路振动的影响规律有详细的研究［10］。图5为轴向载荷T=±104N时的周期管路弯曲振动能带结构，由于频率变化较小，为方便分析，只截取了100 Hz以下的能带结构。

图5中虚线为T=104N时的周期管路弯曲振动能带结构，实线为T=－104N时的能带结构。通过计算可发现在0～1 000 Hz内轴向载荷T=104N时存在三个带隙:47.6 ～87.9 Hz，241.2 ～400.5 Hz和 665.4 ～820.3 Hz;轴向载荷T=－104N时，带隙变为53.5～91 Hz，246.3 ～403.7 Hz和 670.3 ～824 Hz。与图 3 中的数据相比较知轴向压力载荷可以使带隙频率降低，轴向拉力载荷则可提高带隙频率。

5 弹性地基和轴向载荷共同作用对带隙的影响

通过上述研究可知弹性地基使周期管路带隙频率升高，而轴向压力载荷则能降低带隙频率，为方便分析这两种因素对带隙频率的影响比重，下面分析弹性地基和轴向载荷共同作用下周期管路的第一带隙频率变化情况。图6描述了弹性地基和轴向载荷对周期管路弯曲振动第一带隙频率的影响变化曲线。其中方框代表第一带隙的起始频率，圆圈代表第一带隙的截止频率。

图中虚线为地基参数kf=0 Pa时，轴向载荷T对周期管路弯曲振动第一带隙频率的影响曲线。由曲线可知随着T的增大，周期管路弯曲振动的第一带隙起始和截止频率均减小。

一维声子晶体梁弯曲振动的第一带隙起始频率与其单个对称型原胞的固有振动模式完全一致［11］，从而对一维声子晶体带隙特性的分析可以简化为对其单个对称性原胞固有模式的分析。

其中B为铝，A为环氧树脂。当第一带隙的起始频率w=0时，可得到所需轴向载荷T1=8.4×104N。对于图7(c)通过计算可得其屈曲临界载荷［12］T2为7.8×104N。当轴向载荷为T1时，第一带隙的起始频率变为0，此时轴向载荷已超过周期管路的屈曲临界载荷值，结构发生失稳。

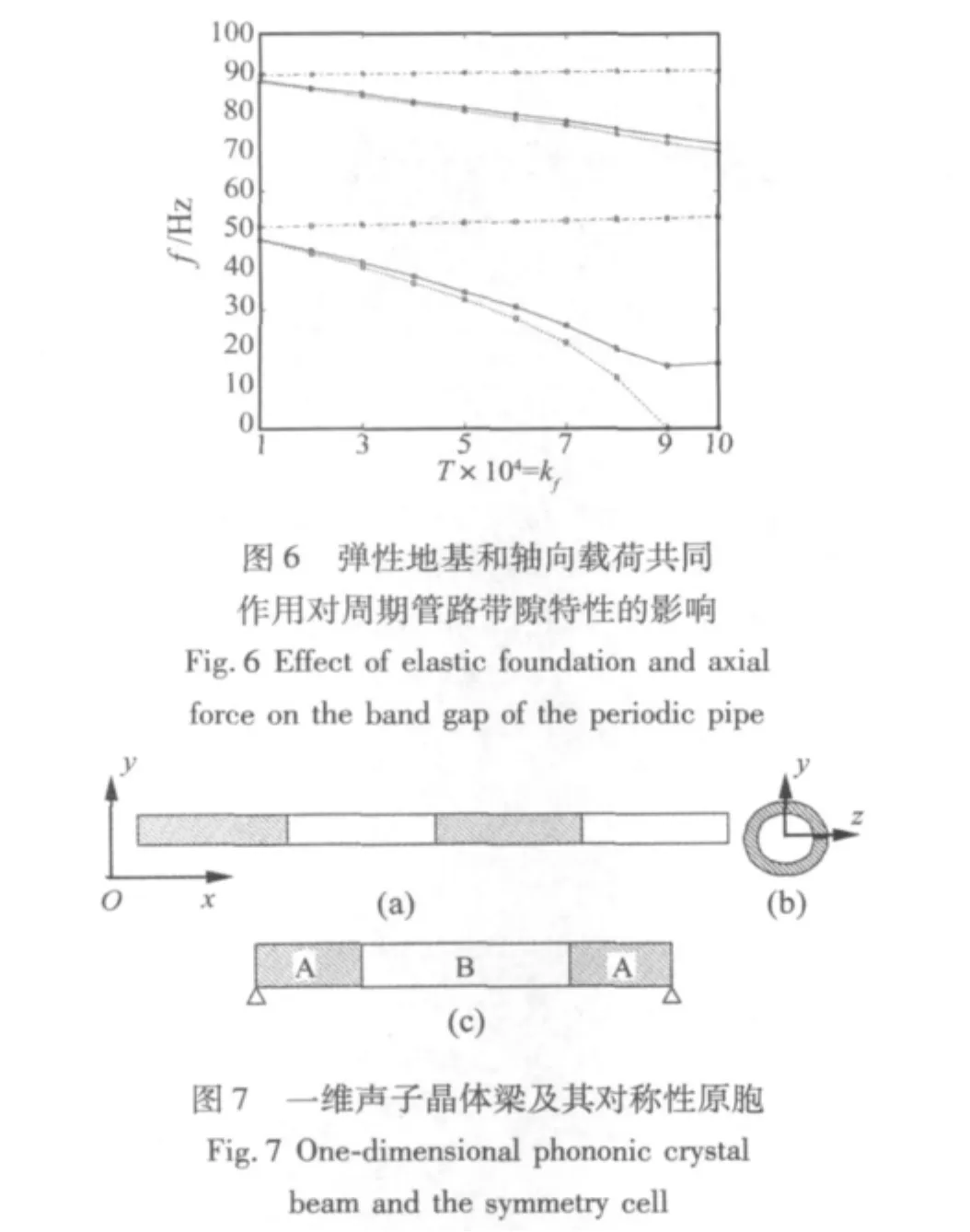
图6中点划线为轴向载荷T为0时，地基参数kf对周期管路弯曲振动第一带隙频率的影响曲线。由曲线可知随着kf的增大，周期管路弯曲振动的第一带隙起始和截止频率均升高，不过变化幅度较小，近似一条直线。

图6中实线为轴向载荷和弹性地基共同作用下，周期管路弯曲振动第一带隙的频率变化曲线。计算中轴向载荷和地基参数变化范围相同，均为104到105。可发现随着轴向载荷和地基参数的同步增大，周期管路弯曲振动的第一带隙起始和截止频率均减小，且变化趋势与虚线相近。当kf=0 Pa，T=105N时周期管路屈曲失稳，当kf变为105Pa周期管路失稳现象消除，这表明弹性地基可以提高管路系统的稳定性。可以通过调节轴向载荷和地基参数，获得所需的带隙范围，实现低频范围内的减振降噪，提高带隙的适应性。

6 结论

本文利用传递矩阵法研究了弹性地基上具有外力载荷的一维充液管路弯曲振动的带隙特性，对弹性地基和轴向载荷共同作用下弯曲振动的带隙变化规律进行了分析。结论如下:

(1)弹性地基上的一维充液周期管路存在弯曲振动带隙，且弹性地基作用使得弯曲振动带隙频率升高。

(2)弹性地基上的管路系统存在一个关键频率，在关键频率以下振动不能传递，但不是带隙的原因。

(3)轴向载荷为拉力时，带隙频率升高;轴向载荷为压力时，带隙频率降低。

(4)弹性地基和外力载荷均可以影响充液周期管路的带隙频率，且轴向载荷对周期管路弯曲振动带隙影响更大，而弹性地基则可以明显提高具有轴向载荷管路系统的稳定性。

因此在工程应用中，可以根据实际需要对地基参数和轴向载荷进行适当调节，实现带隙频率的可调控性，这为充液管路的振动控制提供了新的技术思路。

［1］ 任建亭，姜杰胜.输流管道系统振动研究进展［J］.力学进展，2003，33(3):313－325.

［2］ Winkler E.Die lehre von der elastigitat und festigkeit［M］.Dominicus:Prague，1867.

［3］ Selvadurai A P S. Elastic analysisofsoilfoundation interaction［M］.London:ElesvierScientific Publishing Co，1979.

［4］ 温熙森，温激鸿，郁殿龙，等.声子晶体［M］.北京:国防工业出版社，2009.

［5］ Koo G H.Vibration reduction by using priodic supports in a piping system［J］.Journal of Sound and Vibration，1998，210:53－68.

［6］ Yu D L，Wen J H，Zhao H G，et al.Vibration reduction by using the idea of phononic crystals in a pipe-conveying fluid［J］.Journal of Sound and Vibration，2008，318:193－205.

［7］ 郁殿龙，温激鸿，陈圣兵，等.轴向载荷周期结构梁的弯曲振动带隙特性［J］.振动与冲击，2010，29(3):85－88.

［8］ Mei C.Effect of material coupling on wave vibration of composite Euler-Bernoulli beam structures［J］.Journal of Sound and Vibration，2005，288:177－193.

［9］ 王忠民，冯振宇，赵凤群，等.弹性地基输流管道耦合模态颤振分析［J］.应用数学和力学，2000，21(10):1060－1068.

［10］ 樊丽俭，张瑞平.轴向载荷输流管道的稳定性分析［J］.西北大学学报(自然科学版)，2004，34(2):158－163.

［11］ 蔡 力，韩小云，温熙森.一维声子晶体振动带隙的带边模式研究［J］.机械工程学报，2011，47(9):90－96..

［12］ 单辉祖.材料力学［M］.北京:高等教育出版社，2007.