部分敷设阻尼材料的水下结构声辐射分析

王献忠，孙龙泉，邱忠辉，郑 律

(哈尔滨工程大学 船舶工程学院，哈尔滨 150001)

水下结构如潜艇和鱼雷，是在水中航行的复杂弹性体结构，其内部动力装置的机械振动传递到壳体，进而向周围流体介质传播噪声，从而形成辐射噪声。降低水下航行体的辐射噪声不仅可以提高自身的隐蔽性，而且还可以增大自身声呐系统的探测距离。在壳体表面敷设阻尼层是减少内部机械激励引起结构声辐射的重要声隐身技术之一。考虑到实际的水下航行体结构，由于设备和工艺的原因，使得壳体沿周向不能完全敷设阻尼材料。圆柱壳体是潜艇、鱼雷及其他各种水下航行体的主要结构形式。因而，研究部分敷设阻尼层圆柱壳体的声辐射性能，在工程实践中具有重要的现实意义。

对于低频范围内的敷设阻尼层圆柱壳振动与声辐射问题，国内外有许多学者进行了研究，已取得一定的成果。Laulagnet等［1－2］研究了流体中覆盖有一层粘弹性阻尼材料的有限长圆柱壳的声辐射，在处理肋骨时采用了能量法。陈炜等［3］研究了敷设自由阻尼层的环肋圆柱壳在流场中的声辐射，并讨论了阻尼层各参数对环肋圆柱壳的声辐射影响。陈美霞等［4］研究了内、外壳体敷设粘弹性阻尼材料的有限长加肋双层圆柱壳的振动和声辐射性能。商德江等［5］用有限元软件ANSYS和边界元软件SYSNOISE对双层加肋圆柱壳的水下受激振动与声辐射作了数值计算分析。李鸿芬等［6］讨论了敷设粘弹性阻尼层材料环肋柱壳在流体中受到径向激励时的响应。毛云等［7］利用模态展开技术和Green函数法研究了部分敷设阻尼材料的有限长圆柱壳在流场中的声辐射特性。

但在中、高频范围内，由于计算模型模态密集，结构模型的细微差异对结构响应影响较大。有限元和边界元等确定性方法受到计算机速度和内存的挑战，已不适应于求解高频结构响应的计算。程广利等［8］应用统计能量分析法(SEA)预测中高频段船舶噪声。刘小勇等［9］采用统计能量分析方法，建立水下有限长双层圆柱壳体结构机械噪声预报模型，对统计能量分析重要参数的敏感性进行了一些分析。国内针对圆柱壳体高频辐射噪声的研究多是集中在计算模型的噪声预报上。对于运用SEA方法对敷设阻尼材料水下航行体高频辐射噪声的预报和有效控制的研究较少。本文首先建立了敷设阻尼材料水下航行体SEA计算模型，并通过数值计算分析了结构阻尼参数、阻尼材料敷设比例对水下航行体的降噪效果的影响。通过数值计算结果与该动力舱段模型试验结果的对比，验证了数值计算模型的有效性;通过分析阻尼敷设比例对圆柱壳声辐射的影响，得到有效控制水下结构声辐射的一些结论。

1 统计能量分析方法

统计能量分析(SEA)方法从统计的观点出发，以能量为基本变量，重点研究稳态振动时的平均振动能量在复杂系统里的传递和分布，是研究结构和声场的相互作用及振动在结构间传输的有效方法。

SEA的基本出发点是将一个完整的计算模型离散成N个子系统(包括结构和声场)，在外界激励作用下产生振动时，子系统间通过接触边界进行能量交换，而每个子系统的振动参数如:位移、加速度、声压均可由能量求得，所以“能量”是分析结构噪声的基本未知量。分析的第一步就是确定由相似模态群构成的子系统，这些子系统必须能够清楚的表示出能量的输入、储存、耗散和传输等特性。统计能量分析就是当某个或者某些子系统受到激励而振动时，子系统间就通过接触边界进行能量交换，如此，对每个子系统都能列出一个能量平衡方程，最终得到一个高阶线性方程组，解此方程组求得每个子系统的能量，进而由能量得到需要的各个子系统的振动参数，如位移、速度、加速度和声压等。以此来预测该计算模型的声振响应。各子系统的稳态响应时的能量平衡关系式［10］为:

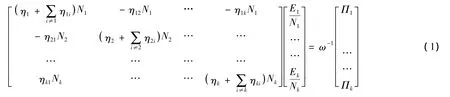
式中:Πi为子系统i的输入功率;ω为系统的平均固有频率;ηi为子系统i的内损耗因子;ηij为子系统i与子系统j间的耦合损耗因子;Ei为子系统i的总能量;Ni为子系统i的模态密度。

通过求解此方程可得到每个子系统的能量，再根据子系统的能量就可以对系统的响应进行估计了。结构子系统，振动均方速度为:

式中:Ei为子系统结构的模态振动能量，Mi为子系统质量。振动速度级为:

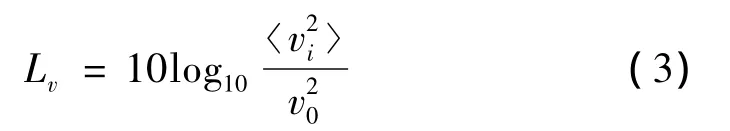
式中:v0=1×10－9m/s为参考速度值，据此相应的可求出计算模型的加速度级。

声场子系统声压均方值为:

声压级为:

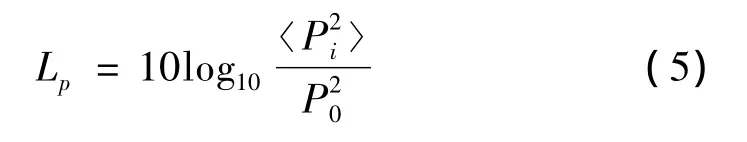
式中:P0=1×10－6N/m2时为水介质中的参考声压。

将统计能量分析方法用于计算水下航行体模型受内部机械激励产生的辐射噪声，首先要根据计算模型的动力学特点，划分水下航行体的子系统，即相似模态振型群。其次确定每个子系统的统计参数，进而求解能量平衡方程组，由求解得到的子系统能量代入式(2)、式(4)中得到对应的声压或者振动响应平均值。

水下航行体的结构比较复杂，根据水下航行体的组成及结构声传递特点，可将舷间及壳体内声腔分别划分为圆柱声腔，将双层圆柱壳中的耐压壳、非耐压壳划分为圆柱壳(弯曲板)子系统，将托板、基座和耐压壳体的前后壁板划分为平板子系统。简化为采用点力模拟机械激励，用距离壳体100 m的半无限流场模拟水下声辐射。这些子系统之间的能量关系如图1所示。最后该双层圆柱壳模型分别由411块板结构子系统，8个声腔子系统组成。

图1 水下航行体的统计能量分析模型Fig.1 Statistic energy analysis model of submarine

2 统计能量分析参数

在统计能量分析模型中，统计能量分析参数主要有:模态密度、损耗因子(包括内损耗因子、耦合损耗因子)、激励的输入功率等。由统计能量分析方法可知，如果系统的参数已知，那么系统的统计能量分析过程将转化为一个代数方程的求解，计算过程就会非常简单，所以较准确的确定每个子系统相应的参数是准确预报计算模型声辐射的前提条件［10］。

2.1 输入功率

由于计算模型中的机械激励为点源，则机械激励作用在基座上的输入功率∏i可由机械阻抗理论导出，由下式确定:

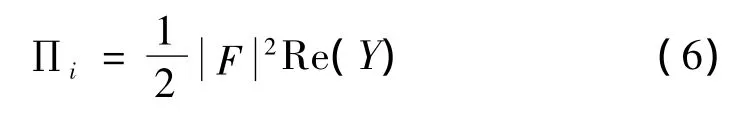
高频时，有限板的激励点导纳与无限板的点导纳相等:

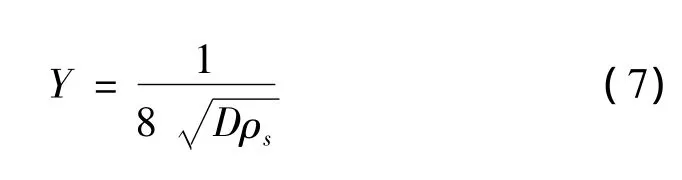
2.2 内损耗因子

在机械结构中，子系统内损耗因子(ILF)ηi是由三种彼此相互独立的阻尼机理成份构成:

式中:ηis表示系统本身材料内摩擦构成的结构损耗因子，只与材料本身有关;对本模型结构材料钢，ηis可取2×10－4;ηir表示系统振动声辐射阻尼形成的声辐射损耗因子为机械阻尼Pt，σ1r为结构的辐射比;ηib表示各子系统边界连接阻尼构成的边界损耗因子。

对于表面敷设阻尼材料的自由阻尼复合结构，计算式为:

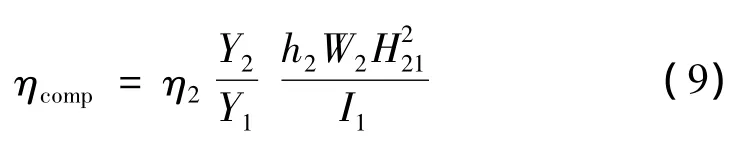
式中:ηcomp为复合结构的结构损耗因子，η2，Y2，h2，W2为粘弹材料阻尼层2的损耗因子、杨氏模量、厚度及宽度，Y1，I1为结构1的杨氏模量及截面惯性矩，H12为结构1和阻尼层2的中性轴之间距离。由式(9)可以计算出敷设阻尼吸声材料复合结构的结构损耗因子ηis。

在实际工程应用［11］中，① 当子系统结构之间为刚性连接时，可以忽略边界损耗因子ηib;② 当子系统为具有高辐射比的孤立单个轻质结构时，ηi≈ηir，当不是轻质结构时ηi≈ηis。③ 非常低的频率区域，ηcomp中以ηis为主;低、中频区域，ηcomp中以 ηir为主;在高频区域，ηcomp中又以ηis为主。这说明ILF的下限是结构损耗因子 ηis。

对敷设阻尼吸声材料的结构损耗因子，其ηis占绝大部分，所以ηi≈ηis;对不敷设阻尼吸声材料的结构，大部分是刚性连接的，可以忽略ηib，其中的平板结构(包括托板、端板和基座)近似计算式为:

其中:a，b根据实际板厚确定。对托板:a=1.82，b=0.7;对端板:a=1.965 6，b=0.7，在中、低频段做声辐射修正即可。

在统计能量分析模型中，声腔子系统i的内损耗因子ηi计算式为:

其中:声场的混响时间TR可利用文献［10］计算得到。

2.3 耦合损耗因子

耦合损耗因子(CLF)ηij是耦合系统在连接处对频率和模态取平均意义的模态间作用力大小的一个度量。水下航行体一般为板与板的连接，因此，子系统之间的耦合连接方式主要为:板与板之间线连接、板与声腔之间面连接、声腔之间的面连接。对于一般的板或板梁组合结构弯曲振动是辐射空气噪声的主要振动形式，所以通常只考虑弯曲振动耦合损耗因子。

描述子系统间的耦合作用可用模态法和波动法来描述，对于波动法耦合损耗因子ηij直接由波传播系数τij导出。对于线连接的两个构件，其CLF为:

式中:l为直线长度，A1为第一子系统的表面积，为板中的波速，τij为波的传递系数，定义为穿过连接线的功率与入射功率之比，以托板子系统1和圆柱薄壳子系统2构成的“T”型系统，经验公式为:

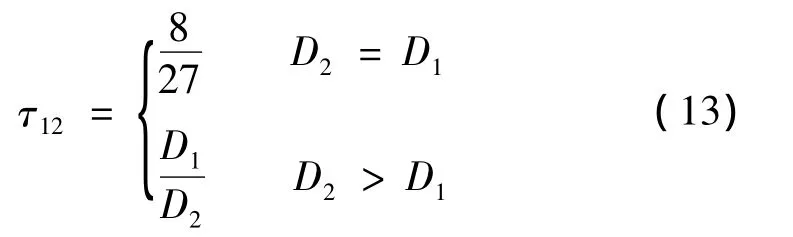
2.4 模态密度

弯曲振动梁的模态密度:

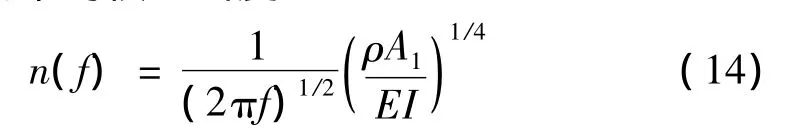
式中:L为梁长，A1为梁的横截面积，ρ为材料密度，EI为梁的抗弯刚度。平板的弯曲振动模态密度为:

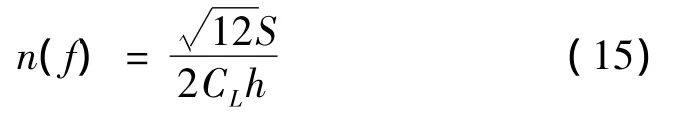
式中:S为平板面积，h为平板厚度，CL为平板的纵波速度。声腔子系统的模态密度为:

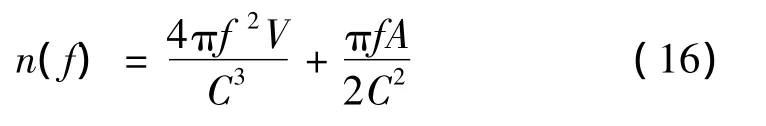
式中:V为容积，A为总表面积，C为声速。

3 敷设阻尼模型的声辐射试验

圆柱壳体是潜艇、鱼雷及其他各种水下航行体的主要结构形式。以动力舱段的大尺度双壳结构模型为实验对象，对部分敷设阻尼材料工况的实验模型在相同激励和相同边界条件下进行激振，测量模型近场辐射声压级，对比分析模型在各种工况下减振降噪的优劣。其中该模型长度为2 m，外壳直径为2.4 m，内壳直径为2 m，文中实验测量用水听器距圆柱壳外板为1 m，其水下深度位置在圆柱壳轴向中部。模型试验是在长50 m、宽15 m、深10 m，其池壁和水面六面安装了消声尖坯的大型消声水池中进行。

本试验分别采用单频激励和声源激励两种激励方式，其中声源发出10～6 kHz的空气白噪声，直接激励模型壳体。考察不同敷设工况下的圆柱壳降噪效果，具体试验工况如表1所示。阻尼吸声材料的杨氏模量为 1.3e8 Pa，密度为 1 290 kg/m3损耗因子取为 0.5。壳体上敷设的阻尼吸声材料的吸声系数随频率变化曲线如图5所示。

表1 试验工况描述Tab.1 Lists of test condition

图3给出了采用SEA方法及文献［5］中方法与试验值的对比结果。从图中可以发现，FEM/BEM方法只适合于低频区域。在高频区域，SEA计算值与试验值吻合较好，说明本文创建的双层圆柱壳SEA模型是有效的。

图4给出了试验模型单频激励下及声源激励下，不同工况下的辐射声压曲线。从图4(a)中可以看出，单频激振时，全敷设阻尼工况声辐射最小。在100 Hz以内频段，四种敷设方式对于圆柱壳辐射噪声没有明显的区别，曲线基本重合在一起。由于100 Hz附近是模型的一阶固有频率，100 Hz左右处结构辐射声压值达到峰值。在100 Hz～2 kHz频段内，全敷设阻尼材料对降低结构辐射噪声效果最明显，内全敷设阻尼工况相对较小，其余两种工况下的声辐射变化相差不大。从图4(b)中可以看出，各工况下的声压曲线变化趋势相同，模型近场声压存在多个峰值点，且各峰值大小量值比较一致，且小于单频激振时的声压值。另外，还可以看出，双壳全敷设时，模型近场声压最小，即全敷设工况的降噪效果最好。

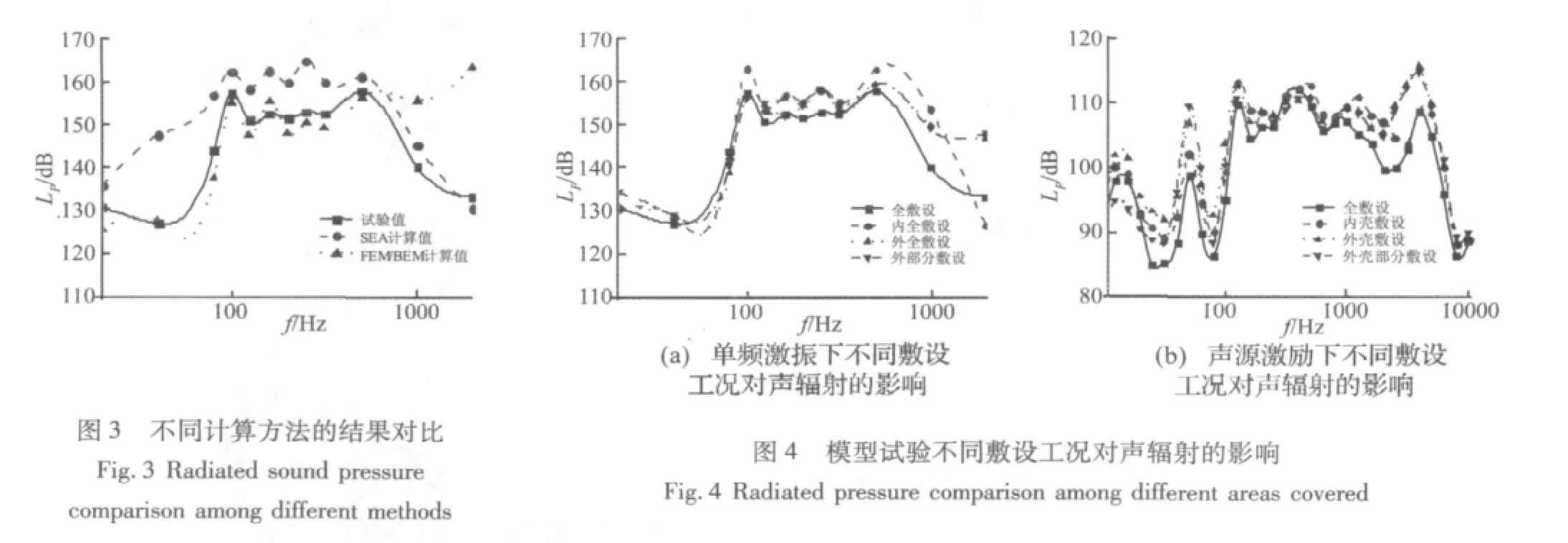
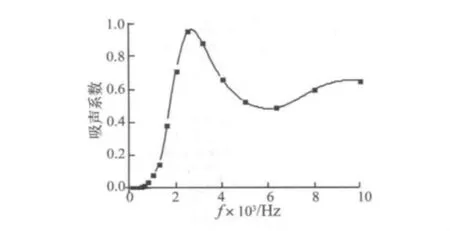
图5 吸声系数曲线Fig.5 Sound absorption coefficient

4 敷设阻尼水下航行体的声辐射分析

本文研究具有五个舱段的水下航行体，包括含基座的动力舱段，其中壳体设置多处舱壁等结构，计算模型如图6所示。钢的杨氏模量E=2e11 Pa;泊松比μ=0.312;密度 ρ=7 840 kg/m3;空气密度 ρ=1.21 kg/m3;海水密度ρ=1 026 kg/m3;空气中声传播速度c=343 m/s;海水中声传播速度c=1 500 m/s。激励源按1/3倍频程分布的单位声功率。激励力仅设置在动力舱段。

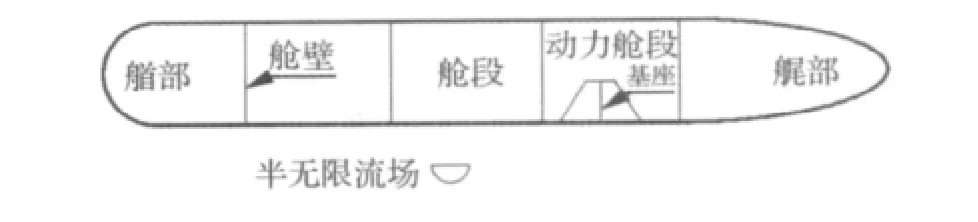
图6 水下航行体计算模型Fig.6 Calculated model of submarine

在本文研究的航行体结构振动问题上，对于系统可得N个线性方程，解此方程组就可以得到各个子系统的能量E，将其代入振速和声压的求解式，就可得到子系统的振动速度和外场声压。

图7为敷设阻尼航行体对应于不同敷设比例时的辐射声压曲线，图8为敷设阻尼材料航行体的降噪效果曲线。阻尼材料为沿周向敷设，敷设比例为沿轴向等间距敷设长度与航行体总长的比值。降噪效果为不同敷设比例工况与不敷设工况声辐射的差值。由图7、图8可以看出:当结构阻尼较低时(η=1%时)，全敷设阻尼航行体的降噪效果要远远好于其他比例的工况。即使阻尼材料敷设比例达到75%，敷设阻尼航行体的降噪效果依然较差，即存在“声泄露”［2］。

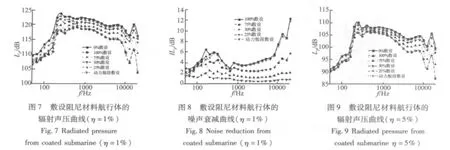
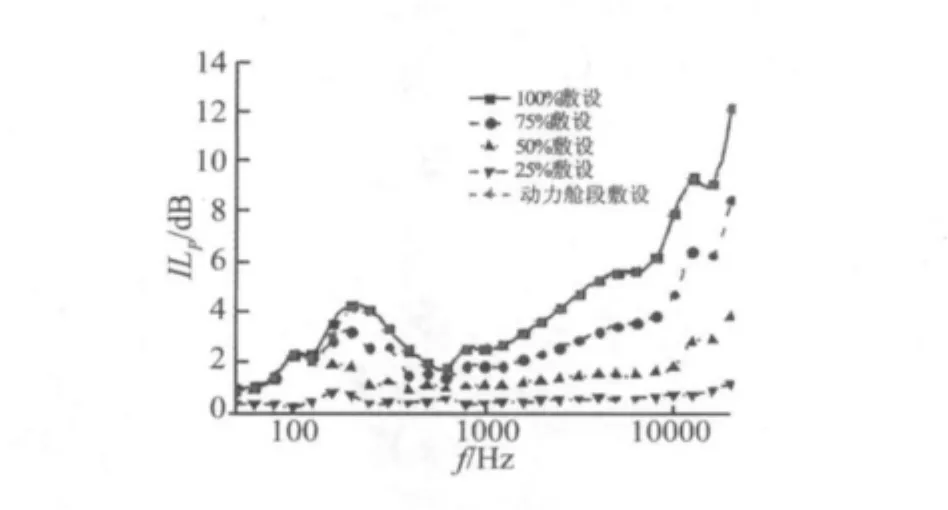
图10 敷设阻尼材料航行体的噪声衰减曲线(η=5%)Fig.10 Noise reduction from coated submarine(η =5%)

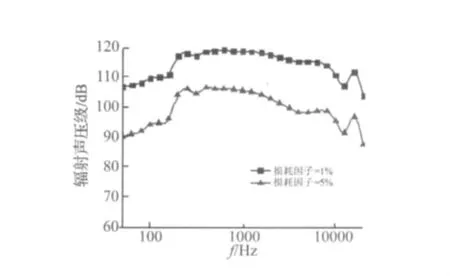
图11 敷设100%阻尼时航行体辐射声压曲线Fig.11 Radiated pressure from wholly coated submarine

当结构阻尼相对较高时(η=5%时)，敷设阻尼材料航行体的声辐射特性及降噪效果曲线如图9、图10所示。从图9、图10中可以看出:由于阻尼损失系数变大(由1%提高到5%)，阻尼的降噪效果就可有较大提高，75%敷设工况其降噪效果可高达8dB以上。原因为当结构阻尼不断增大时，振动能量主要集中在激励源附近，传递到未敷设壳体部分的能量减少，“声泄露”现象得到明显改善。同时通过对比图11可以看出，不同损耗因子对水下航行体辐射噪声影响较大。当损耗因子由1%变为5%时，航行体辐射声压在整个频带均有所下降。

无论结构阻尼η=1%，或η=5%，只要将动力舱周围敷设完整的阻尼层，即可有效阻止结构辐射噪声的传递，此时的阻尼层降噪效果同100%敷设时的效果相差不大;且随着结构阻尼的增大，两者的降噪效果差异逐渐减小。

5 结论

通过对水下航行体结构进行SEA分析和试验研究，表明统计能量方法可以分析敷设阻尼材料双层圆柱壳的声辐射响应。通过分析结构阻尼参数和模型试验结论如下:

(1)结构损耗因子较小时，与100%敷设工况相比，局部敷设工况会出现“声泄露”，提高结构损耗因子，对减小结构“声泄露”有帮助。

(2)敷设阻尼结构对中高频机械激励具有明显降噪效果，对低频降噪效果较差。

(3)声源激振时，各工况下的声压曲线变化趋势相同，阻尼材料在整个频带都有较好的降噪效果。

(4)通过模型试验测试结果表明:阻尼吸声材料敷设在外壳比敷设在内壳的降噪效果好。

(5)SEA方法在中高频部分的计算结果与实验值吻合较好，计算精度好于FEM/BEM方法，低频段后者较好。

［1］ Laulagnet B，Guyader J L.Sound radiation from finite cylindrical coated shells by means of asymptotic expansion of three－ dimensional equations for coating［J］.J.Acoust.Soc.Am，1994，96(1):277－286.

［2］ Laulagnet B，Guyader J L.Sound radiation from finite cylindrical coated shells，partially covered with longitudinal strips of compliant layer［J］.J.of Sound and Vibration，1995:723－742.

［3］ 陈 炜，骆东平，张书吉，等.敷设阻尼材料的环肋柱壳声辐射性能分析［J］.声学学报，2000，25(1):27－32.

［4］ 陈美霞，骆东平，周 锋，等.阻尼材料敷设方式对双层壳体声辐射性能的影响［J］.声学学报，2005，30(4):296－301.

［5］ 商德江，何祚镛.加肋双层圆柱壳振动声辐射数值计算分析［J］.声学学报，2001，26(3):193－201.

［6］ 李鸿芬，骆东平.自由层阻尼环肋柱壳在流场中的稳态响应［J］.中国造船，1996，133(2):59－69.

［7］ 毛 云，谢官模.水下部分覆盖阻尼材料圆柱壳的声辐射性能［J］.武汉理工大学学报，2005，27(5):21－49.

［8］ 程广利，伍先俊，朱石坚.基于Auto SEA的船舶噪声统计能量分析仿真［J］.海军工程大学学报，2005，17(3):70－73.

［9］ 刘小勇，盛美萍，行晓亮，等.双层圆柱壳噪声预报及统计能量参数灵敏度分析［J］.振动与冲击，2007，26(7):50－53.

［10］ Lyon R H.Statistic energy analysis of dynamic systems［M］.Cambridge:MIT Press，1975.

［11］ 姚德源，王其政.统计能量分析原理及其应用［M］.北京:北京理工大学出版社，1997.