含初始弯曲裂纹转子的振动分析

邹 剑，董广明，陈 进

(1.青岛农业大学 机电工程学院，青岛 266109;2.上海交通大学 机械系统与振动国家重点实验室，上海 200240)

转子系统是航空、电力、机械、化工、纺织等工业部门旋转机械的关键性部件，随着旋转机械日益向高速、轻型、复杂结构、重载、大功率、长周期运行方向的发展，导致转子的振动形态多变、应力状态复杂、轴向温度剃度分布过大以及工作介质的腐蚀加剧等，从而使转子在运行过程中极有可能出现横向裂纹并造成机毁人亡的灾难性事故，因而有必要深入地研究裂纹转子系统的动力学特性，利用现代振动测试与分析技术对转子系统进行在线监测与故障诊断。

为计算转轴横向裂纹的柔度，将应变能释放率理论与线性断裂力学、转子动力学相结合获得较理想的结果;Papadopoulos［1］描述了应变能释放率的基本理论与使用中的延伸与限制，给出了多种不同的裂纹识别方法。林言丽等［2］对现有裂纹转子刚度模型进行了简略的总结，提出了两种原理不同、裂纹张开区域不同的确定刚度方法，试验发现应力强度因子为零法能更好地反映裂纹转子的刚度变化。Gasch［3］提出了简单铰链裂纹模型，将裂纹的张开与闭合状态表示为方波函数，很好地描述了裂纹转子周期变化的刚度及其稳定性，在裂纹转子动力学建模和无损检测中得到了广泛的应用。冷小磊等［4］应用Monte-Carlo随机模拟法，分析了白噪声扰动下裂纹转子刚度变化、转速比等参数对系统分岔及混沌行为的影响，发现在拟周期与混沌解及其临近的分叉参数区间，随机扰动对系统响应有着较为显著的影响，而周期解处则较小。DAI等［5］考虑了周期激励作用下不对称粘弹性支撑下的非线性裂纹转子，采用 Floquet-Lyapunov理论研究了系统的线性、非线性动力稳定性，讨论了不同因素对主不稳定区的影响。罗跃纲等［6］利用求解非线性非自治系统周期解的延拓打靶法和Floquet理论，研究带有裂纹——碰磨耦合故障的具有三轴承支承的双跨弹性转子系统的周期运动的稳定性与失稳规律，认为双跨裂纹转子系统以倍周期分叉形式失稳，双跨碰磨转子系统以Hopf分叉形式失稳。

工程实际中，由于制造安装误差或运行中热效应的原因，会使转轴存在着一定的初始弯曲，进而导致转子动挠度增加，机组的振动加剧，甚至引发转子与静子之间的碰磨。基于简单铰链裂纹模型，建立了含初始弯曲裂纹转子的无量纲动力学模型;对比了含初始弯曲裂纹转子与无初始弯曲裂纹转子谐波频率成分的差异，研究了系统的亚临界共振特性，采用Floquet理论分析了含初始弯曲裂纹转子的稳定性。

图1 裂纹转子横截面Fig.1 Cross section of cracked rotor

1 动力学模型的建立

质量 m的 de Laval转子，简支于长L无质量的弹性轴上。假定，裂纹位于转子的根部并且重力占优。建立图1所示裂纹转子的动力学方程:

转子的刚度矩阵为:

式中，对于匀变速裂纹转子有φ=ωt。

裂纹开闭修正函数Θ可表示为［3］:

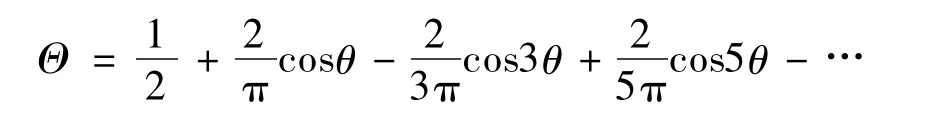
式中，θ=φ+β，研究中只考虑了级数的前四项。

令［x y］T=［Δx Δy］T+［xst0］T，在重力占优的情形下，式(1)转变为;

引入变量 τ=ωnt，Ω =ω/ωn，将式(2)转变为无量纲形式:

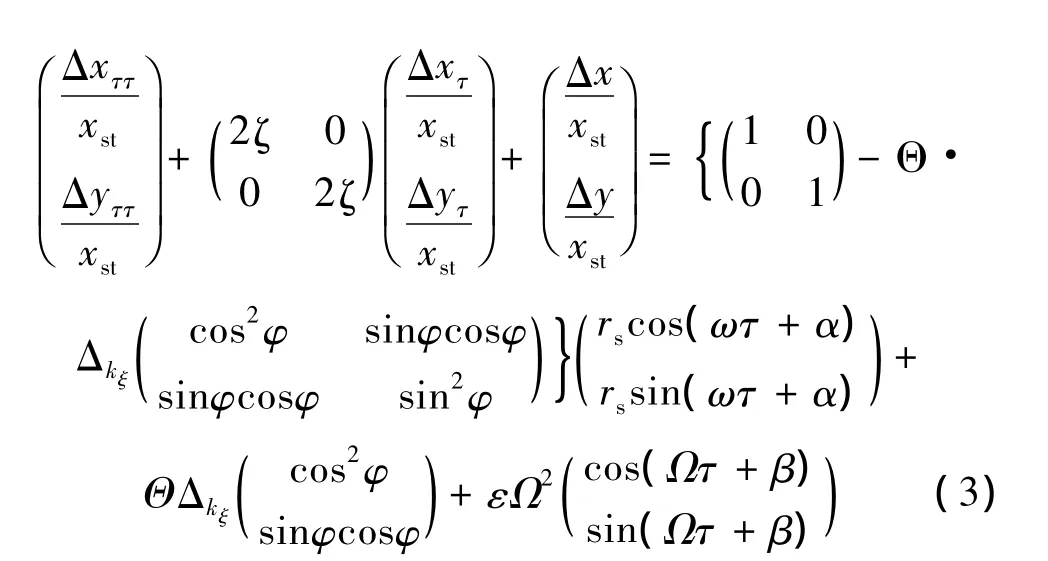
2 亚临界共振

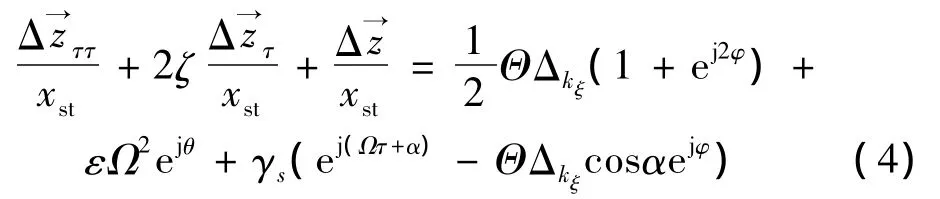
等式右边各项依次为裂纹激励、质量偏心激励、与裂纹无关以及与裂纹相耦合的初始弯曲激励。

将裂纹开闭修正函数Θ按欧拉方程展开，有:

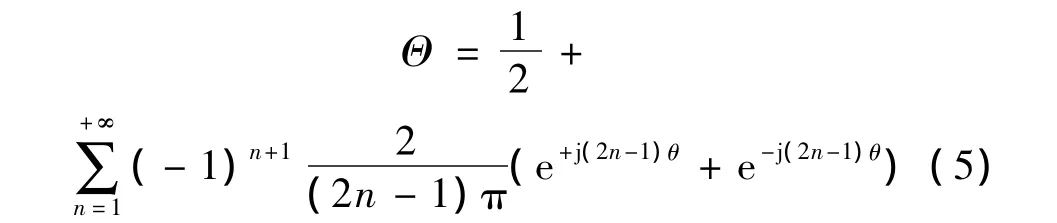
将式(5)代入式(4)，得:

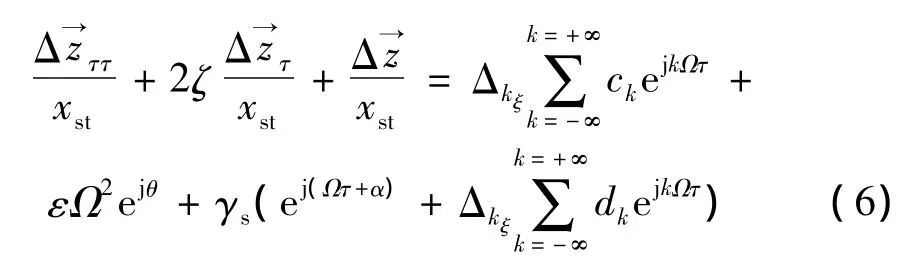
利用含初始弯曲裂纹转子的解析表达式，可以对比无初始弯曲裂纹转子与含初始弯曲裂纹转子频率成分的差异。无初始弯曲裂纹转子仅仅存在着由裂纹引起的1，2，2n－1，…(n=2，3，4，…)等谐波成分，而含初始弯曲裂纹转子则同时还存在着由初始弯曲导致的1，2，2n，…(n=2，3，4，…)等谐波成分。由于含初始弯曲裂纹转子系统存在着1，2，n，…(n=3，4，…)等高次谐波分量，相应的必然存在着高次谐波的1/n(n=1，2，3，…)亚临界共振。含初始弯曲裂纹转子的1/2，1/3亚临界共振的频谱如图2所示，可知在亚临界共振时1次谐波分量占主导作用，而相应的高次谐波分量起着次之的作用。不考虑不平衡、直流分量以及与裂纹无关的初始弯曲激励，令α=β=0，分别得到裂纹激励、与裂纹相耦合的初始弯曲激励各谐波分量的参与因子ck、dk，如表1与表2所示;可以看出:裂纹激励与初始弯曲激励的1，2次谐波的参与因子大于3，4次谐波的，并且正进动分量的参与因子大于反进动的。

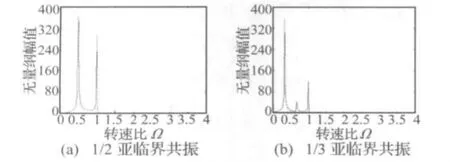
图2 含初始弯曲裂纹转子的频谱分析Fig.2 Frequency spectra of cracked rotor with initial deflection

表1 裂纹激励的参与因子Tab.1 Participation factor of crack excitation

表2 初始弯曲激励的参与因子Tab.2 Participation factor of initial deflection

3 稳定性分析

为了研究含初始弯曲裂纹转子的稳定性，考虑式(2)所示运动微分方程的齐次方程:

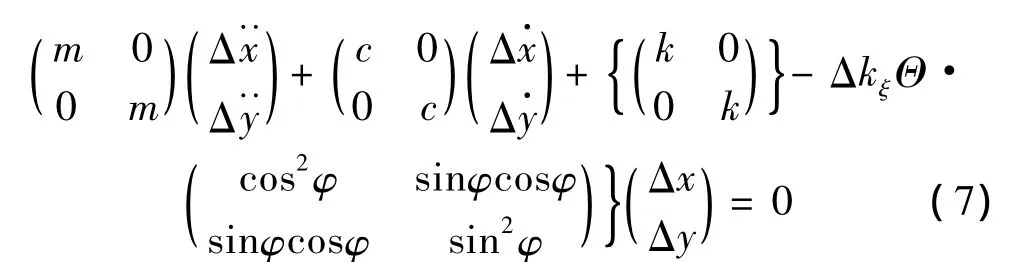
对式(7)进行无量纲化处理，得:

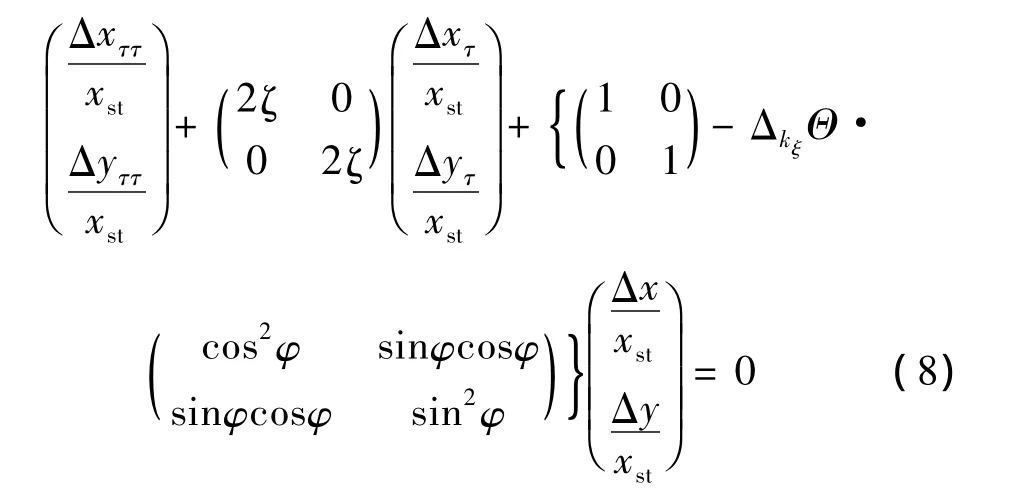
采用状态空间表示法，式(8)改写为:

式中，状态矢量X为:

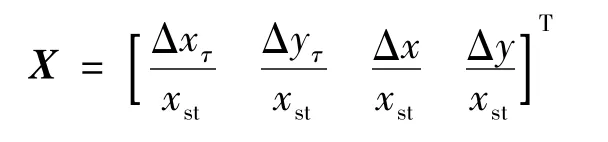
系统矩阵B为:

结合Floquet理论，可得:

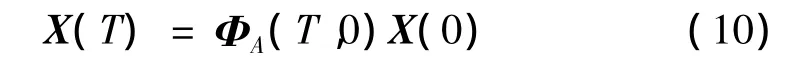
数值积分可计算得到含初始弯曲裂纹转子系统的周期转换矩阵 ΦA(T，0)。

为研究状态矢量之间的关系，假定:

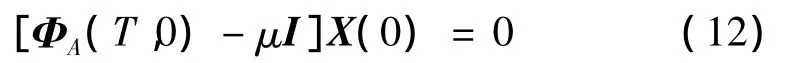
将式(11)代入式(10)，得到Floquet特征值问题:求解式(12)可得到周期转换矩阵 ΦA(T，0)的特征值μ。

利用式(9)～式(12)可以研究含初始弯曲裂纹转子的稳定性随裂纹相对刚度变化Δkξ、转速比Ω以及阻尼比ζ的变化关系，如图3所示(图中阴影部分表示转速不稳定区)。由图3可见，裂纹的存在导致转子系统的稳定性发生变化，主要区别在于含初始弯曲裂纹转子系统由单一不稳定转速变为不稳定转速区，并且不稳定转速区的宽度随着相对刚度变化Δkξ的增大而增加;阻尼则有抑制转子系统不稳定的作用，随着阻尼比ζ的增加不稳定转速区变窄甚至消失。进一步深入分析图3发现:在浅裂纹情形下，含初始弯曲裂纹转子在转速比 Ω =1/4，1/3，2/5，1/2，2/3，1，2 附近出现不稳定转速区，并且不稳定转速区在转速比Ω=2/5，2/3，1，2附近比较明显;而阻尼对于抑制转子系统的不稳定作用显著，即便是在小阻尼的情形下含初始弯曲裂纹转子也仅仅在转速比Ω=2/3，1，2附近出现不稳定转速区。稳定性分析表明:当裂纹转子系统启停车时，必须保证较大的加速度才能通过参数不稳定转速区(Ω=2/3)、主临界不稳定转速区(Ω=1)以及二次临界不稳定转速区(Ω=2)。

4 结论

(1)基于简单铰链裂纹模型，建立了含初始弯曲裂纹转子的无量纲动力学模型。

(2)经解析求解对比了含初始弯曲裂纹转子与无初始弯曲裂纹转子谐波频率成分的差异，发现系统存在着 1，2，n，…(n=3，4)等高次谐波分量，相应的必然存在着高次谐波的1/n(n=1，2，3，…)亚临界共振。

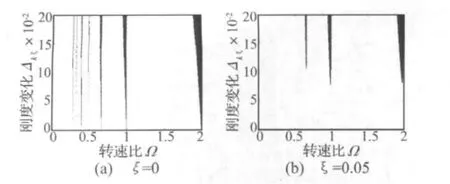
图3 含初始弯曲裂纹转子的稳定性Fig.3 Stability of cracked rotor with initial deflection

(3)采用Floquet理论分析了含初始弯曲裂纹转子的稳定性，发现:在浅裂纹情形下，含初始弯曲裂纹转子在转速比 Ω =1/4，1/3，2/5，1/2，2/3，1，2 附近出现不稳定转速区，并且不稳定转速区在转速比Ω=2/5，2/3，1，2附近比较明显，而阻尼对于抑制转子系统的不稳定作用显著，即便是在小阻尼的情形下含初始弯曲裂纹转子也仅仅在转速比Ω=2/3，1，2附近出现不稳定转速区。

附 录

符 号

B——系统矩阵

c——阻尼

ck——裂纹激励参与因子

dk——初始弯曲激励参与因子

e——质量偏心

I——单位矩阵

k——无裂纹转子的刚度

kx、ky——x、y 方向的弯曲刚度

kxy、kyx—— x、y 方向的交叉刚度

Δkξ——裂纹转子ξ方向刚度变化量

Δk——刚度相对变化率ξ

rs——初始弯曲

X——状态矢量

xoy——惯性坐标系

xst——静态弯曲

T——周期

ω——角频率

ωn——系统固有频率

α——初始弯曲角

β——裂纹法向与质量偏心间的夹角

γs——相对初始弯曲

φ——转角

ζ——阻尼比

Θ——裂纹开闭修正函数

ε——相对质量偏心

ΦA(T，0)——周期转换矩阵

μ——特征值

下标 τ、ττ——对 τ的一阶、二阶导数

ξoη——旋转坐标系

［1］ Papadopoulos C A.The strain energy release approach for modeling cracks in rotors:a state of the art review ［J］.Mechanical Systems and Signal Processing，2008，22(4):763－789.

［2］ 林言丽，褚福磊.裂纹转子的刚度模型［J］.机械工程学报，2008，44(1):114－120.

［3］ Gasch R.A survey of the dynamic behavior of a simple rotating shaft with a transverse crack ［J］.J.Sound and Vibration，1993，160(2):313－332.

［4］ 冷小磊，孟 光，张 韬，等.考虑随机扰动时裂纹转子系统的分叉与混沌特性［J］.振动工程学报，2006，19(2):212－218.

［5］ Dai L M，Chen C P.Dynamic stability analysis of a cracked nonlinear rotor system subjected to periodic excitations in machining［J］.Journal of Vibration and Control，2007，13(5):537－556.

［6］ 罗跃纲，闻邦椿.双跨转子——轴承系统裂纹——碰磨耦合故障的稳定［J］.机械工程学报，2008，44(4):123－127，132.