基于CFD/CSD耦合的颤振与动载荷分析方法

谢 亮，徐 敏，李 杰，蔡天星

(1.西北工业大学 航空学院，西安 710072;2.西北工业大学 航天学院，西安 710072)

颤振是一种极具破坏性的气动弹性现象，可能导致飞行器在短时间内解体性破坏。因此颤振的计算是气动弹性领域内十分重要的一项内容。传统的颤振计算中采用求解线化速度势方程［1]计算非定常气动力，仅能考虑气动力的线性效应，当飞行器处于跨声速、高超声速阶段或者结构出现大变形时气动力的非线性效应比较明显，则其计算结果可信度不足。目前计算流体力学(Computational Fluid Dynamics，CFD)技术已发展得较为成熟，它与计算结构动力学(Computational Structural Dynamics，CSD)的结合为气弹分析提供了强有力的工具，故而CFD/CSD耦合方法已经成为当前气弹仿真的主流手段［2－4]。然而采用CFD/CSD耦合算法的计算效率较低，为此建立起CFD/CSD全耦合系统的降阶模型(Reduced order model，ROM)有其必要性［5]。气动弹性学家 Dowell［6]将目前应用于气动弹性领域的降阶模型分成两类:一类是基于模态的方法，另一类是基于信号的方法。在后一类ROM中，基于Volterra级数的降阶模型应用较为广泛。在上世纪90年代，NASA的 Silva［7]首先利用脉冲响应辨识 Volterra核，并使用特征实现算法构建非定常气动力模型，取得了不错的效果。其后，Raveh针对脉冲响应存在数值不稳定的问题，改用阶跃响应辨识Valterra核，文献［5] 指出采用阶跃辨识得到的一阶核包含了二阶核中的非对角分量，因而能体现更多的非线性。

除计算颤振临界速度外，气动弹性分析还要承担飞行器在动态气动载荷与自身惯性力耦合作用下的动态载荷计算的任务。因为动载荷的计算是结构动态设计的关键技术之一，它为结构响应计算、结构的动态设计与故障分析提供了可靠的依据。目前工程上并不作动载荷的计算［8]，仅求解飞行器的静气弹响应方程，计算出静变形情况下的气动载荷，并乘上一个安全系数作为飞行器的动态载荷。目前使用CFD/CSD耦合方法进行颤振分析已经比较成熟，但是用此手段进行飞行器动载荷的分析还比较少见。仅见有文献［9] 进行了超声速情况下舵面的动载荷分析。

本文采用CFD/CSD耦合算法建立了气弹仿真系统，详细论述了仿真过程中提取动态载荷(包括气动载荷与惯性载荷)的方法。基于系统辨识的方法，使用Volterra级数建立了降阶模型，提供了快速计算颤振边界的手段。分别采用CFD/CSD全耦合方法和ROM计算了AGARD 445.6机翼的颤振边界，并与实验数据进行了对比，验证了计算程序的可靠性。在此基础上采用ROM分析了一型带边条平直翼的颤振边界，使用CFD/CSD耦合方法计算了此机翼在飞行动压下的气弹响应，结果表明即使是在颤振边界内仍有可能出现极限环振荡(Limit cycle oscillations－LCO)。对于0.8马赫，迎角13°情况下出现的LCO情况，分析了其响应过程中的动载荷情况。

1 基于CFD/CSD耦合的气弹仿真

1.1 计算结构动力学方程

将结构模型离散化之后通过非保守系统的拉格朗日方程可以得到如下的结构动力学方程:

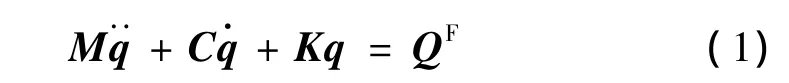
其中M，C，K分别为结构质量矩阵、阻尼矩阵和刚度矩阵，QF为结构外激励。本文中采用振型叠加法求解上述方程。通过求解特征方程Kφi=λiMφi，获得系统的特征值 λ1，…，λN和特征向量 φ1，…，φN，忽略对系统的实际响应贡献较小的高阶振型，保留低阶n个振型，组成振型矩阵 Φ =［φ1，φ2，…，φn] ，则式(1)可近似为如下的n阶方程:

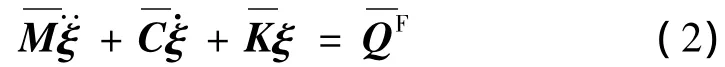
式中，M=ΦTMΦ，C=ΦTCΦ，K=ΦTKΦ分别为广义质量、广义阻尼和广义刚度矩阵。ξ为广义位移，满足:q为广义激励力。

1.2 非定常气动载荷求解

对于方程(1)的右端项QF，即非定常气动载荷，采用CFD方法求解。积分形式的Euler方程为:

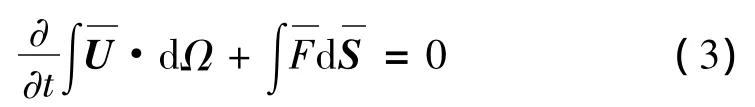
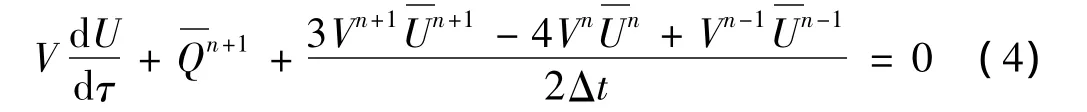
1.3 CFD/CSD耦合算法

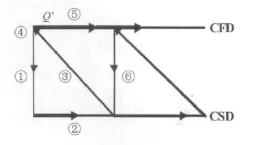
图1 CFD/CSD耦合方式Fig.1 CFD/CSD coupling method

采用松耦合算法在时域内分别求解流体、结构动力学方程，交错时间推进获得耦合系统的响应，其流程图如图1。这种算法的最大好处是能充分利用现有的计算流体动力学和计算结构动力学的程序，只要增加流体－结构数据交换模块即可，从而保持程序的模块化。虽然结构求解器和流体求解器都具有二阶及二阶以上的精度，但是此种耦合方法由于流体和结构积分的不同步势必造成数值误差，当积分时间步取得较大时计算结果有可能失真。为解决这个问题，对松耦合方法作了如下改进［5]:

在气动弹性计算中非定常气动力和结构位移一般都呈连续变化。为此，对图1中的步骤①做如下修正:通过时刻的气动力(均已知)做三点抛物插值，拟合得出tn～tn+1时间内气动力关于时间的二次函数。将这个随时间变化的气动力代入结构动力学方程(1)，推进求得tn+1时刻的结构参数。这个修正在很大程度上提高了CFD/CSD松耦合计算的精度。

结构流体数据交换采用无限平板样条(Infinite plate spline，IPS)方法［10]，动网格采用无限代数插值(Transfinite interpolation infinite，TFI)实现。

1.4 基于Volterra级数的非定常气动降阶模型。

Volterra级数是一个无穷级数，小扰动下，Euler方程计算得到的非定常气动力可以表示为二阶Volterra级数形式，时域内离散形式为:

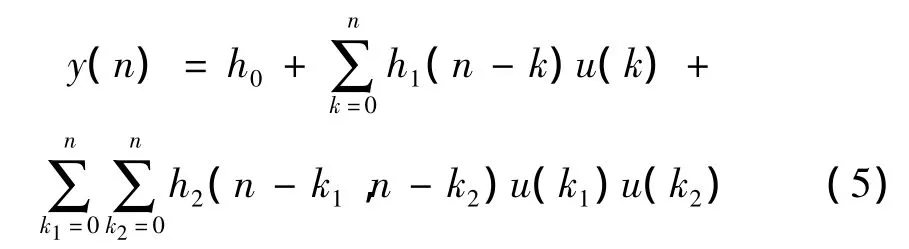
采用阶跃响应辨识非定常气动力，给CFD/CSD耦合系统如下阶跃响应:可辨识得到包含二阶核对角分量及部分非对角分量的近似一阶核为:

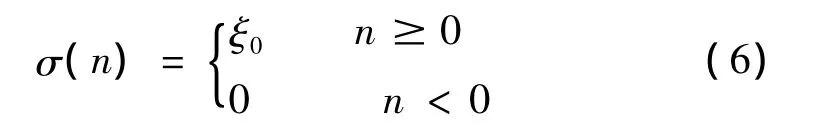
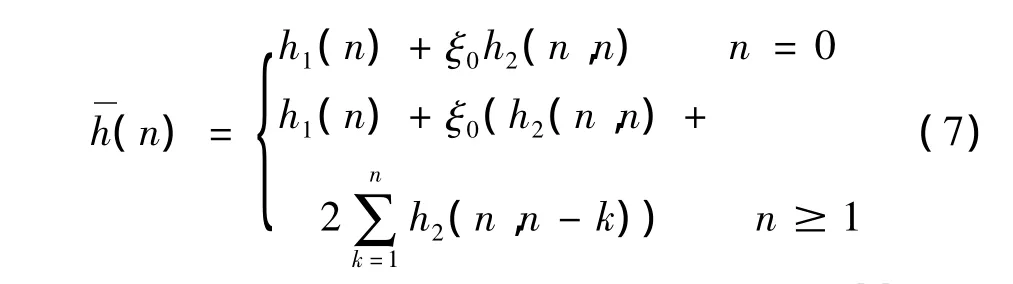
利用得到的volterra核通过特征实现算法［5]可以得到以状态空间形式表示的非定常气动力的降阶模型，此状态空间模型以广义位移为输入，以广义力为输出，通过此模型计算方程(1)的右端项(即气动力载荷)，结构动力学方程仍然采用模态叠加法，则可以得到整个气动弹性系统的低阶状态空间模型，通过调整动压分析系统的稳定性来求颤振边界。

1.5 动态载荷的计算

飞行器动态载荷计算是结构设计和故障诊断的重要环节，仅通过静气弹结构设计有时并不能满足动强度要求。传统的气动弹性分析方法通过频域或时域识别方法来确定气动载荷［1]，然而当结构变形较大或者飞行器处于跨声速、高超声速阶段时，非定常气动力存在明显的非线性效应，只能通过CFD技术实现气动载荷提取。本文采用CFD/CSD耦合计算飞行器的动态响应，提取了非定常气动力载荷和惯性载荷，实现了动载荷分析。

对于式(1)，右端项表示飞行器所受到的气动载荷，除此外，飞行器还受到自身惯性力施加的惯性载荷，即方程(1)左端第一项M·q·。飞行器所受到的真实载荷即由这两项组成:

在CFD/CSD耦合计算的每一个时间步中，分别提取出气动载荷QF与惯性载荷，按式(8)求和，得总载荷。

气动载荷的求解依靠CFD系统，在双时间推进求解流场的每一真实时间推进过程中，当内层迭代(即伪时间步推进)收敛后，利用物面的压强沿物面作数值积分即可求得该时刻的瞬态气动载荷。惯性载荷的求解有两种方案，一种是将求解得到的随时间变化的瞬态气动载荷加载到CSD系统上进行动态响应分析，从而求解得到整个响应过程中惯性载荷及总载荷，同时可以获得此过程中的瞬态应力，文献［9] 即采用的此种方案。本文采用的是另一种方法:将使用有限元方法求得的CSD系统的总体质量阵M导入CFD/CSD耦合系统，利用计算动态惯性载荷。由于CFD/CSD耦合中CSD系统采用的是模态迭加法，故而无法直接按求解惯性载荷，但是注意到q=Φξ，则惯性载荷的求解可使用下式:

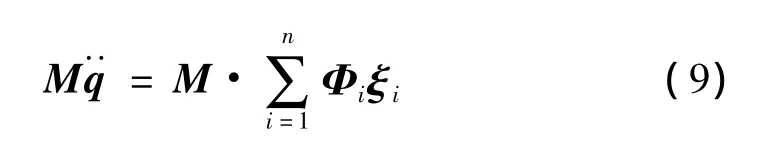
上式中，下标i表示第i阶模态，Φi与ξi分别是该阶模态对应的振型与广义加速度，n表示截取的模态阶数。M，Φi由有限元方法进行模态分析得到，而ξi由CFD/CSD耦合方法求解，利用求解得到的广义速度ξi作数值差分求解得到。

2 算例分析

2.1 算例1:AGARD 445.6验证算例

分别采用CFD/CSD耦合方法与ROM求解了AGARD 445.6机翼的颤振边界。首先采用有限元法对AGARD 445.6进行模态分析，选择前四阶模态组成解耦后的结构动力学方程。按前述方法将之与CFD系统耦合建立CFD/CSD时域仿真系统。建立ROM时，计算模态仍选取前四阶模态，对CFD/CSD耦合系统施加阶跃响应，响应幅值取1.0E－4，辨识物理时间步长取1.0E－4s，计算1000个时间步长内的非定常气动力，按前述方法建立起系统的低阶状态空间模型。CFD/CSD耦合算法及ROM计算结果与实验值的对比见图2，可见计算值与实验值［11]相符较好，且与国内外计算结果一致［2－5]，由此验证了CFD/CSD耦合算法与程序的准确性与可靠性。CFD/CSD耦合方法与ROM计算结果几乎重合，表明在颤振计算中可以使用ROM代替CFD/CSD全耦合系统，实现颤振边界的快速求解，对本算例，CFD/CSD耦合仿真计算时间约为降阶模型计算的10～100倍。

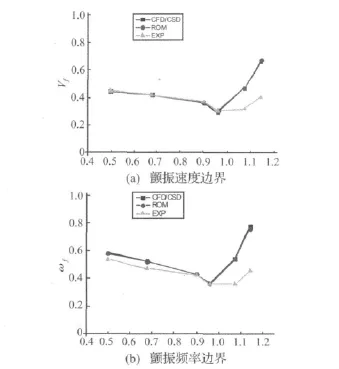
图2 AGARD445.6机翼颤振边界Fig.2 Flutter boundary of AGARD 445.6

2.2 算例2:带边条的平直翼的颤振及动载荷分析

机翼几何形状及有限元模型见图3，表面气动网格见图4.采用有限元法其进行模态分析，截取前四阶模态组成解耦后的CSD系统。前四阶模态频率及类型见表1。各阶模态的变形通过IPS方法插值到气动网格上的变形见图5，可见变形网格光滑，插值效果优良。

图3 机翼有限元模型Fig.3 FEM model

图4 表面气动网格Fig.4 CFD grid of case 2

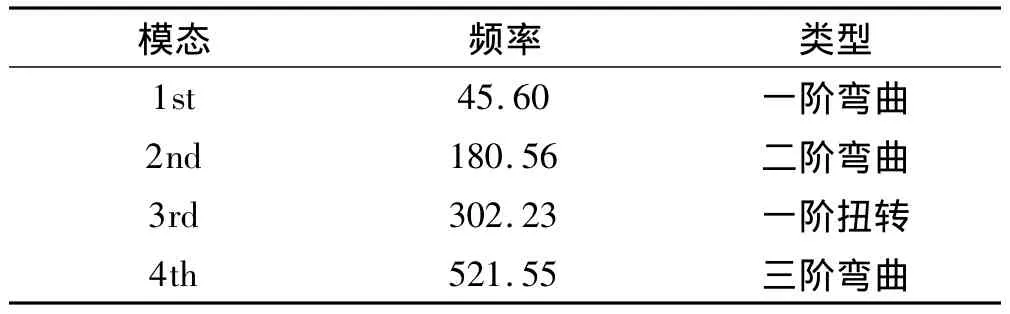
表1 算例1结构前四阶模态Tab.1 Lower 4 structure modes of case 1

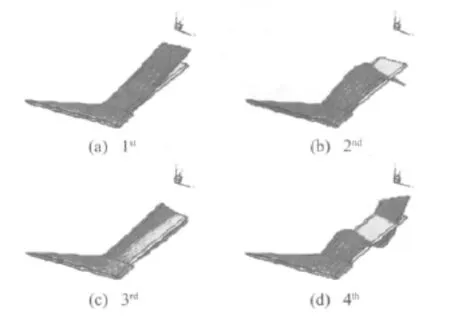
图5 模态插值得到机翼的变形Fig.5 Deformation by interpolation from structure modes

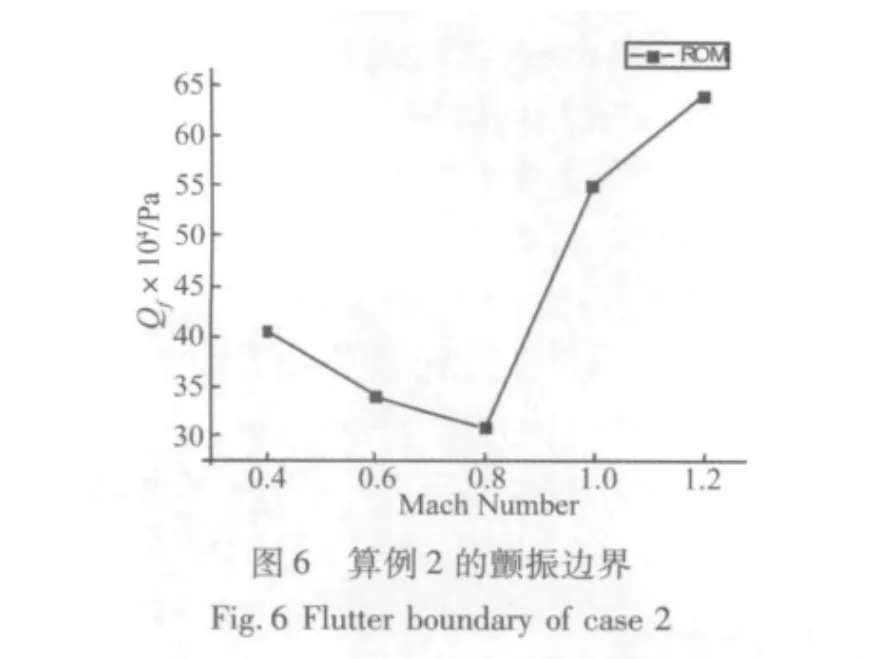
鉴于ROM的准确性已由AGARD 445.6标模算例得到了验证，为求快速获得结果，故而此处直接使用ROM进行颤振分析，得到此机翼颤振边界如图6所示。

采用CFD/CSD耦合方法计算了机翼在飞行动压下的气弹响应情况。由于计算的颤振临界动压都远远大于飞行动压(以海平面的参数计算，因此时的动压是最严荷的)，故而在计算的数个状态下，响应都是收敛的，然而在马赫数0.8，迎角13°的情况下，出现了第一、二、四阶模态(弯曲)收敛，第三阶模态(扭转)不收敛的现象，如图7(图中也给出了最后几个周期内二、三、四阶广义位移的局部放大图)，这与一般意义上的弯扭耦合颤振发散呈现出不同的特点。

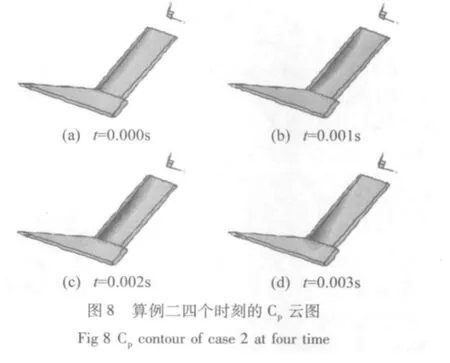
分析位移响应曲线，从幅值上判断，气弹响应过程中开始阶段以弯曲响应为主，但是弯曲响应(一、二、四阶模态)是收敛的，而第一阶扭转模态发散，最后呈现出极限环振荡的形式，使响应过程变为以扭转响应为主的阶段。为详细确定其发散的原因，给出在一个第一阶扭转模态周期(0.003 31 s)内四个时刻的表面压力系数Cp的分布，如图8。发现在此周期内的大部分时刻，其表面Cp云图与第三阶模态(图5(c))基本重合。另一方面，此时飞行动压为45 352 Pa，远远小于图6所示的马赫数0.8时的颤振动压(308 000 Pa)，因此，此种不收敛的响应不应该归于颤振发散。故而可以确定这是在非定常气动力作用下的强迫振动。对于这种情况，由于其在一个较长时间历程内都维持着较小的振幅，因而其对结构的影响应当进一步通过提取其响应过程中的动态载荷来分析。

按1.5节所述方法提取出响应过程中的动态载荷信息，分别计算惯性载荷、气动载荷，按式(8)求总载荷，并分别求其对翼根的弯矩，结果如图9示。计算所得气动载荷在以弯曲响应为主的阶段峰值为275 N·m，进入极限环后峰值为335 N·m，惯性载荷在以弯曲响应为主的阶段峰值为22 N·m，进入极限环后峰值为11 N·m，总载荷在弯扭耦合阶段的峰值为285 N·m，进入极限环后峰值为325 N·m。由图可见，在响应前期的以弯曲响应为主的阶段，机翼受到的总载荷大于气动载荷，而当响应进入扭转响应为主的阶段时，由于单纯的扭转导致的附加气动力起阻振作用，故而总载荷小于气动载荷，是气动载荷与惯性载荷之差。在本算例中，定常气动载荷为230 N·m，动态载荷的峰值是它的1.4倍左右，这与文献［9] 所给出的超声速舵面在高超声速情况下总载荷是定常气动载荷的3倍左右的结论不同，则可认为动态载荷与静态载荷之间的关系与飞行器的构型、飞行条件相关，因此在飞行器设计过程中，除了要进行静态载荷分析外，仍有必要分析动态载荷情况。而使用CFD/CSD耦合的方法提供了提取弹性响应过程中动态载荷的有效手段。

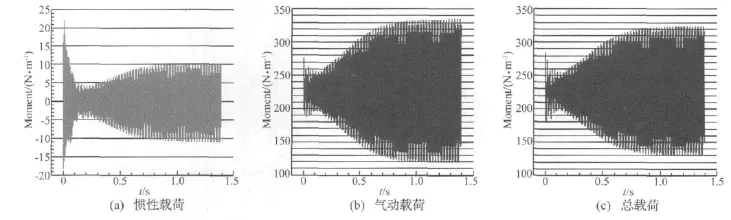
图9 载荷对机翼翼根的弯矩Fig.9 Blending moment toward wing root

飞行器也有可能出现极限环振荡，对此应当予以注意。提取了响应过程中的动态载荷信息，结果表明气弹响应过程中，弯曲响应导致的瞬态总载荷比气动载荷要大，而扭转响应过程中的总载荷小于气动载荷，因此在飞行器设计过程中，除了进行静态载荷的计算外，仍有必要分析动态载荷，而基于CFD/CSD耦合而建立起来的气动弹性时域仿真系统提供了提取出响应过程中动态载荷(包括气动载荷与惯性载荷)的有效手段。

3 结论

采用CFD/CSD耦合方法计算了AGARD 445.6机翼的颤振边界，计算结果与实验结果相符较好，由此验证了本文所采用的CFD/CSD耦合算法的准确性与可靠性。基于Volterra级数建立了CFD/CSD耦合系统的降阶模型，实现了颤振的快速求解，AGARD 445.6算例的结果表明ROM的计算结果与CFD/CSD全耦合方法的结果基本一致，而效率上提高了一到两个数量级。

用CFD/CSD耦合方法模拟了机翼在飞行动压下的气弹响应历程，结果表明即使飞行动压远小于颤振边界，由于空气动力的非线性与结构的非线性因素，飞行器也有可能出现极限环振荡，对此应当予以注意。提取了响应过程中的动态载荷信息，结果表明气弹响应过程中，弯曲响应导致的瞬态总载荷比气动载荷要大，而扭转响应过程中的总载荷小于气动载荷，因此在飞行器设计过程中，除了进行静态载荷的计算外，仍有必要分析动态载荷，而基于CFD/CSD耦合而建立起来的气动弹性时域仿真系统提供了提取出响应过程中动态载荷(包括气动载荷与惯性载荷)的有效手段。

［1] 管 德.非定常空气动力计算［M] .北京:北京航空航天大学出版社，1991.

［2] Liu F.Calculation of wing flutter by a coupled fluid-structure method［J] .Journal of Aircraft，2001，38(2):334 －342.

［3] Elizabeth M，Lee-Rausch ，Batina H T.Calculation of AGARD wing 445.6 flutter using navier-stokes aerodynamics［R] .AIAA，93－3476，1993.

［4] Bennett R M，Edwards J W.An overview of recent developments in computational aeroelasticity［R] .AIAA，1998，98 －2421.

［5] 曾宪昂.模型降阶技术在气动弹性中的应用研究［D] .西安:西北工业大学，2008.

［6] Dowell E H，Hall K C.Modeling of fluid-structure interaction［J] .Annual Review Fluid Mechanics，1993，33:445 －490.

［7] Silva W A.Application of nonlinear systems theory to transonic unsteady aerodynamic responses［J] .Journal of Aircraft，1993，30(5):600 －668.

［8] 管 德.飞机气动弹性力学手册［M] .北京:航空工业出版社，1994.

［9] 蔡天星，徐 敏，姚伟刚，等.基于CFD/CSD耦合的超声速舵面动载荷分析［J] .工程力学，2011，28(3):245 －250.

［10] Goura G S L .Time marching analysis of flutter using computational fluid dynamics ［D] . University of Glasgow，2001.

［11] Yates E C.AGARD standard aeroelastic configurations for dynamic response I-Wing 445.6 ［R] .Agard Report No.765，The 61stMeeting of the Structures and Materials Panel at Oberammergau，Germany:September，1985.