地下矿山采场爆破效果评价的未确知测度模型

曹铭宇,许杨丰,孙鹏伟,陈 刚,李丽香

(中金岭南有色金属有限公司凡口铅锌矿, 广东韶关市 512325)

地下矿山采场爆破效果评价的未确知测度模型

曹铭宇,许杨丰,孙鹏伟,陈 刚,李丽香

(中金岭南有色金属有限公司凡口铅锌矿, 广东韶关市 512325)

针对地下矿山采场爆破效果评价中许多不确定性因素,借鉴未确知测度理论,将爆破效果与其影响因素之间的关系作为未确知系统,提出地下矿山采场爆破效果评价的未确知测度模型。以某铅锌矿为例,构造了适于爆破效果预测指标的测度函数,选取大块率、每米崩矿量和炸药单耗作为爆破效果评价的3大指标参数,同时引入信息熵理论确定各指标的权重,依照置信度识别准则对其风险等级进行判定,最后得出采场爆破效果等级的评价结果,并与模糊数学方法和工程实际情况进行了对比。用该模型对八方山铅锌矿试验采场爆破效果评估的结果与实际情况一致,且评价结果直观、准确可靠,具有信息利用率高的优点。

采场爆破;爆破效果;评价模型;未确知测度;熵;置信度识别准则

爆破效果的优劣直接影响到采场和周边围岩的稳定性,开挖面的完整性及矿山的经济效益,而爆破效果的主要影响因素是爆破参数及矿岩的物理力学性质,在实际工作中要根据每次的矿岩物理力学性质和爆破效果及时调整爆破参数,因此,开展爆破效果的评价研究具有重大现实意义。

长期以来,采场爆破效果的评价没有清晰的界限,以往的评价一般由专业人员做定性分析,有很大的主观性;有的评价方法常常采用单项指标,有很大的片面性。加上其影响因素具有多样性、复杂性和非线性的特点,很难提出准确通用的判别准则,鉴于此,建立一种多参数综合评价模型对爆破效果进行正确预测对采矿设计具有重要意义。如方崇[1]利用突变理论对光面爆破效果进行综合评价;李东强[2]、蒲传金等[3]建立了爆破效果综合评价的模糊层次分析评估模型。上述新的理论和方法有其自身的特点,同时也存在一定不足,针对模糊数学、突变理论等应用于采场爆破效果评价时,存在评价空间不能有序分割,确定的指标权重受主观影响大的缺陷,运用未确知理论构建了采场爆破效果的未确知测定模型[4],并用于实例评价,取得了良好的效果。

1 未确知测度评估原理

设采场爆破效果评价对象ξ有n个,则评价对象空间ξ＝{ξ1,ξ2,…,ξn}。对于每个评价的对象ξi i(＝1,2,…,n)有m个单项评价指标空间,即X＝ {X1,X2,…,Xm},则ξi可表示为m维向量ξi＝{xi1,xi2,…,xim},其中,xij表示采场爆破效果评价指标的测量值。对每个子项xiji(＝1,2,…,n;j＝1,2,…,m),假设有p个评价等级{R1,R2,…,Rp}。记评价空间为D,则D＝{R1,R2,…,Rp}。设Vk(k＝1,2,…,p)为第k级评价等级,且k级比k+1级采场爆破效果等级“高”,记为Vk＞Vk+1。若满足R1＞R2＞…＞Rp,则称{R1,R2,…,Rp}是评价空间D的一个有序分割类[]。

若μijk＝μ(xij∈Vk)表示测量值xij属于第k个评价等级的程度,且要求满足:

(1)非负有界性,0≤μ(xij∈Vk)≤1;

(2)归一性,μ(xij∈D)＝1;

则称其为未确定测度,简称测度[4]。在区间[ai,ai+1]上对应的未确知测度函数的表达式分别为:

在上述各函数表达式中,μi(x)在点ai左半区间上的值取0,在区间[ai+1,ai+2]上与μi+1(x)在(ai,ai+1]上的图象相同;μi+1(x)在[ai-1,ai]上的图象与μi(x)在[ai,ai+1]上的图象相同,μi+1(x)在ai+1左半区间上取值为0。

设wj表示测量指标Xj与其他指标相比具有的相对重要度,需满足:0≤wj≤1,且Σmwj＝1,称wjj＝1

为Xj重,称w＝{w1,w2,…,wm}为指标权重向量,根据熵确定权重[4-5],即:

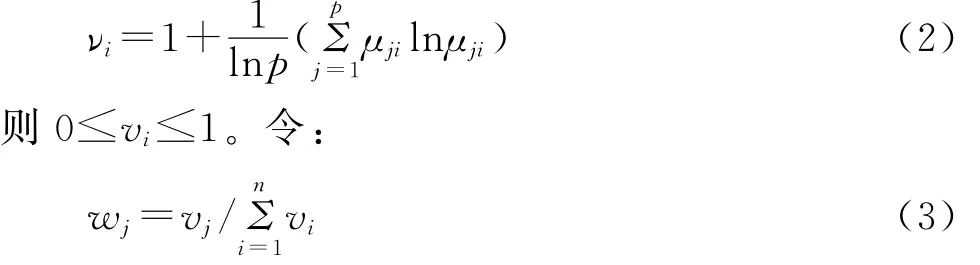
令μik＝μ(Xi∈Vk)为评价样本属于ξi第k个评价类Rk的程度,则有

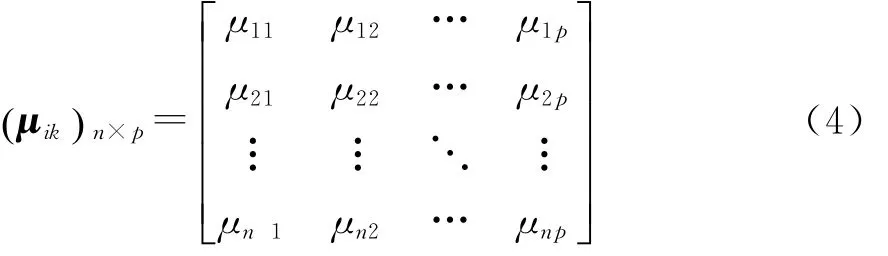
为多目标综合未确知测度评价矩阵,称{μi1,μi2,…,μip}为ξi的多指标综合测度评价向量[]。

当{R1,R2,…,Rp}有序时,最大隶属度识别准则不再适用。为此采用置信度准则[4-6],设λ为置信度,取值范围通常为0.5＜λ＜1,且满足R1＞R2＞…＞Rp时,其识别模型为:

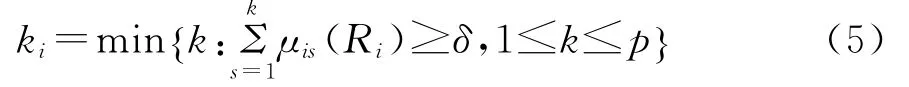
取k值直到满足式(5),则xi属于Rki类或Rki级。

2 地下采场爆破效果评价的未确知测度模型

2.1 确定评价因子

影响爆破效果评价的因素有很多,建立采场爆破效果的未确知测度评估模型时,还需考虑分析资料的易获性和代表性,参考有关爆破效果评判指标体系研究[1-3],选取大块率、每米崩矿量和炸药单耗作为爆破效果评价的3大指标参数作为未确知测度模型评估指标,其分级判据指标如表1所示[2]。在确定评价等级分类方案时,根据部分学者研究成果[2],将爆破效果分为很好(V1)、较好(V2)、一般(V3)和较差(V4)4个类别,如表1所示。其评价流程如图1所示。

表1 爆破效果评价指标及分级标准

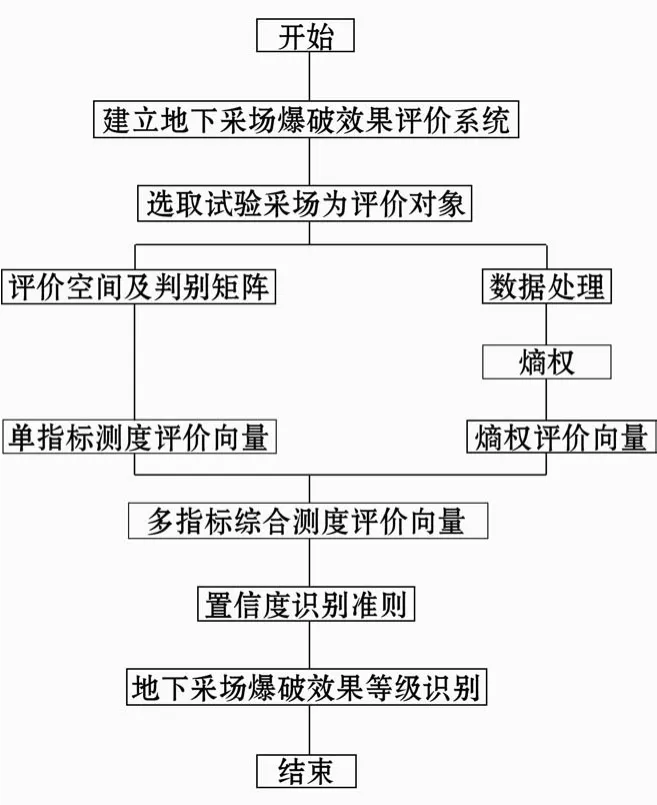
图1 采场爆破效果的未确知测度评价流程

2.2 爆破效果评价的未确知测度模型的建立及评价

为了验证本文提出的基于熵权未确知测度理论的爆破效果评价方法的有效性和实用性,以八方山铅锌矿某试验采场为例[2],任意取其中9次爆破,采用专家评估与计算方法,得到该采场9次的爆破效果数据,如表2所示。

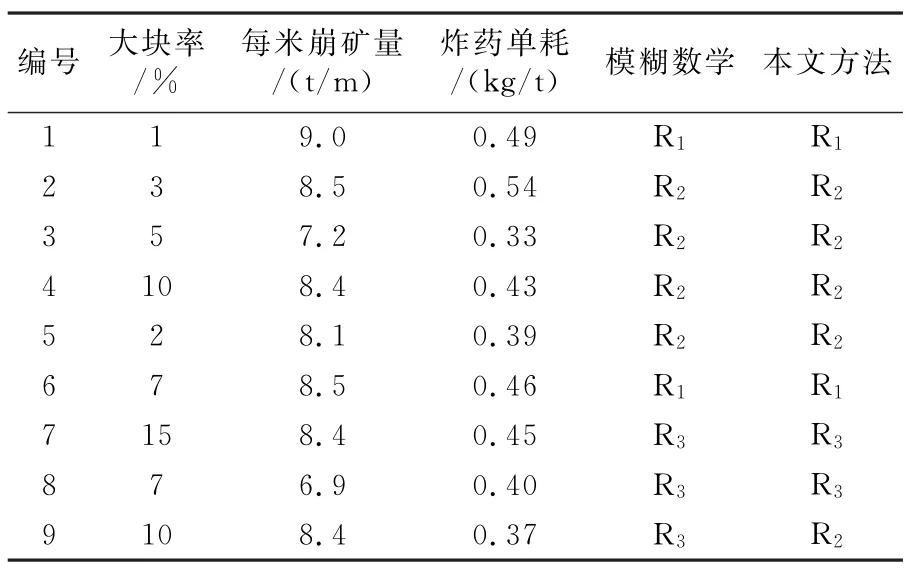
表2 试验采场爆破效果数据

以第1次爆破为例,根据单指标测度函数的定义和表1构建单指标测度函数以便求得各评价指标的测度值。其各自的单指标测度函数分别见图2。由表1中各因子的取值,根据以上单指标测度函数(见图2),可求得该地段评价对象的单指标测度评价矩阵为:

利用信息熵理论确定各指标权重,据式(2)～(3)可得评价指标的权重向量w＝{0.36,0.28, 0.36}。由此求得样本1的多指标综合测度评价向量:{0.610,0.194,0.177,0.019}。

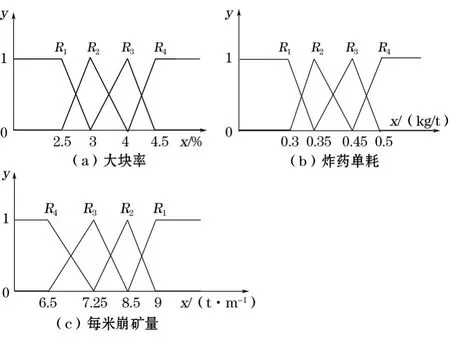
图2 单指标测度函数曲线

2.3 属性识别评价结果分析

取置信度λ＝0.6,由属性综合测度评价式(5)可以判别其爆破效果等级为R1,即样本1的爆破效果好,并与模糊数学析法[2]的评价结果进行对比,如表2所示。从表2可以看出,该采场爆破效果评价样本未确知测度评价结果较好,与实际情况基本吻合[2]。从而说明本文采场爆破效果评价模型的有效性和可行性。所以,将未确知测度分析模型应用于采场爆破效果评价的判定中完全可行,高效可靠,具有较高的实用价值。在采场爆破效果评价中,未确知测度评价方法与其它评价方法相比,未确知测度满足“归一性条件”及“可加性原则”,因而评价结果是科学的。另未确知测度方法注意了评价空间的“有序性”,给出了比较合理的置信度识别准则,使评价结果更清晰合理。并且采用信息熵确定各指标权重,最大限度地利用了源数据的有效信息,避免了评价过程中的单纯主观臆断和片面性。

3 结 语

(1)针对采场爆破效果评价与其影响因素间高度的非线性复杂关系,引入未确知数学和信息熵理论,通过深入地挖掘采场爆破效果的各种因素,选取大块率、每米崩矿量和炸药单耗作为爆破效果评价评价的3大指标参数,同时引入信息熵理论确定各指标的权重,依照置信度识别准则对其风险等级进行判定,最后得出采场爆破效果等级的评价结果,并与模糊数学方法和工程实际情况进行了对比。

(2)本文所建立的采场爆破效果评价的未确知测度模型,计算方法简单,评价结果与实际情况较吻合,为采场爆破效果评价方法提供了一种崭新的途径。值得一提的是,采场爆破效果评价结论的准确性与可信度,关键取决于所采用的评价指标及如何构造未确知测度函数,需深入了解采场爆破机制及环境效应等,详实分析各影响因素对采场爆破效果的影响,构造更加广泛适用的未确知测度函数,提高采场爆破效果评估模型的可靠性。

[1]方 崇.基于燕尾突变理论光面爆破效果的综合评价[J].爆破,2010(4):40-42,47.

[2]李东强.地下矿山采场爆破效果的综合评价[J].金属矿山, 2005(S):79-81.

[3]蒲传金,肖正学,郭学彬.爆破效果综合评价的模糊层次分析法模型[J].矿业快报,2004,35(11):12-15.

[4]史秀志,周 健.隧道围岩分级判别的未确知均值聚类模型[J].土木建筑与环境工程,2009,31(2):62-67.

[5]史秀志,周 健,董 蕾,等.未确知测度模型在岩爆烈度分级预测中的应用[J].岩土力学与工程学报,2010(29):2721-2726.

[6]薛剑光,周 健,史秀志,等.基于熵权属性识别模型的岩体可爆性分级评价[J].中南大学学报(自然科学版),2010,41(1): 251-256.

2012-03-09)

曹铭宇(1985-),男,湖南郴州人,助理工程师,主要从事采矿设计与技术管理工作。