基于SEM模型的个人住房抵押贷款违约影响因素实证研究
姜明辉,陈昊洁,袁天琪
(哈尔滨工业大学 管理学院,黑龙江哈尔滨 150001)
基于SEM模型的个人住房抵押贷款违约影响因素实证研究
姜明辉,陈昊洁,袁天琪
(哈尔滨工业大学 管理学院,黑龙江哈尔滨 150001)
将结构方程(SEM)模型引入到个人住房抵押贷款违约风险影响因素的研究,改进基于线性、回归方法中只针对违约风险与影响因素之间(潜变量与显变量)的关系的研究,增加影响因素之间(显变量与显变量之间)的相互路径分析,在一个更全面的路径系统中找出主要的影响因素,提出预防和控制违约风险的方法。
个人住房抵押贷款,违约,结构方程模型
一、引言
作为居民住房资金重要组成部分之一的个人住房抵押贷款,逐渐成为金融机构特别是银行机构的重要信贷资产,但是高居不下的不良贷款率限制了金融业的发展。对于商业银行而言,对消费者还贷进行评估,将能更有效地规避风险,对提高消费信贷发放的积极性具有重要意义。而运用实效、科学的评估方法巩固完善评估体系至关重要。
本文在分析国内外个人住房抵押贷款违约风险影响因素发展现状及其方法应用的基础上,参考国内外已有的指标体系,构建适合中国国情的个人住房抵押贷款违约影响因素结构模型。结合目前我国商业银行业务系统中所获取的实际数据情况,确定所使用的指标,建立结构方程模型。并根据实证结果分析,从商业银行个人住房抵押贷款违约影响因素控制和提高风险管理两个层面探讨了如何加强和改善我国个人住房抵押贷款违约风险管理措施。
应用结构方程模型来研究个人住房抵押贷款违约风险,建立个人住房抵押贷款违约意向概念模型,通过分析软件Amos修正、拟合模型,找出反映违约意向的潜变量和显变量,针对违约意向的复杂性特点,增加了单一指标的多路径指向性,通过路径分析,得出最优的政策保障体系。在计算过程中,结构方程模型分析方法特有的信度和效度检验,也确保了方法的科学性和有效性。
二、文献回顾
该理论最早于上世纪60年代由西方学者Allen Jung F首先提出,运用实证领域统计和计量的方法研究违约风险影响因素。随后,各种方法被使用到该领域。例如:回归分析 Roger Burrows(1998)[1]及 Quercia、Roberto G. 和 Michael A.Stegman(1992)[2];方差分析刘春红(2000)[3];Logistic分析 Lawrence、Edward C.和 Nasser Arshadi(1995)[4]及王福林(2005)[5]、马宇(2011)[6];博弈分析施锡锉、张森(2002)[7]等。
研究的趋势和角度主要集中在借款人特征、家庭财务负担、贷款特征等方面。Webb Bruce G.(1998)[8]及王震勤、王维才、李秋妍(2008)[9]等分析不同借款人特征对逾期风险的影响,得出反映借款人特征的个人特征因素,包括年龄、受教育程度、职业等对消费者是否违约占很大的权重。而具有代表性的 Santos Silva J和 J.Murteira(2000)[10]及汪利娜(2001)[11]在衡量体现家庭财务负担特征的主要因素借款人收入,借款人家庭成员数量、贷款总金额等后,发现家庭财务负担对贷款违约的影响最大。而另一个重要影响因素便是贷款特征,可以用贷款价值比、还款期限、还款方式、担保方式等因素来衡量。其中贷款价值比LTV(Loan To Valuation)是最为重要的因素。Nothaft,Frank E. 和 Gcorge H. K.Wang(1993)[12]及刘萍(2002)[13]在运用多种数学方法比较讨论后,得出贷款因素比对违约风险最具解释力。
从国内外的相关文献内容可以看出,国外学者从不同的角度对个人住房抵押贷款违约风险进行了大量的研究,实证领域的统计和计量的方法被广泛应用。在研究个人住房抵押贷款违约风险的决定性因素方面主要从贷款特征、借款人特征、住房特征等进行探讨,得出了许多适合国家信用保障的方法。
本文运用结构方程模型讨论个人住房抵押贷款违约影响因素,有效地避免了使用回归方法而产生的参数估计的偏差,增加了因子分析、路径分析等特征,在分析中既处理了测量误差,同时又可以分析潜变量、显变量之间的结构关系。更好地说明借款人特征、家庭财务负担、贷款特征3个潜变量如何影响个人住房抵押贷款违约意向,及早规避风险。
考虑到当地经济文化背景以及实务操作上的影响,选取不同城市的多家商业银行的实际信贷档案资料中的部分资料进行实证研究。由于选取的样本多为离散变量,未能完全彻底地刻画客户的特征,因此计算结果会出现一定的误差,因此,在选取样本时通过增加样本的数量来弥补这一不足。
三、结构方程模型的应用及假设
(一)结构方程的应用
作为统计分析方法的一个重要发展方向,建立结构方程模型求解越来越被广泛的使用。结构方程模型的应用实质是使用联立方程求解的过程,整个建模分析过程都是动态的形式。通过每次模型计算的结果推理模型建造的合理性,再根据以往经验和原有模型的拟合度结果分析去修正模型,最终得到最符合实际、最合理的模型。
结构方程模型的原理体现在建立联立方程组中,包括测量方程与结构方程两类方程[14]。
(1)测量方程。测量方程是表示观测变量x,y与潜变量η,ξ之间关系的方程组。

其中:x-:由外生指标组成的向量
y-:由内生指标组成的向量
Λx-:外生指标与外生潜变量之间的关系
Λy-:内生指标与内生潜变量之间的关系
δ-:外生指标的误差项
ε-:内生指标的误差项
η-:内生潜变量
(2)结构方程。结构方程是表示潜变量与潜变量之间关系的方程组。其中,ξ-:外生潜变量
B-:内生潜变量之间的关系
Γ-:外生潜变量对内生潜变量的影响
ζ-:结构方程的残差项
根据两组方程,设定模型并计算各个参数。
(二)模型的假设
1.构建模型的假设条件
通过对国内外学者的研究结果进行归类分析,结合我国银行系统实际情况,本文假设借款人特征、家庭财务负担、贷款特征对违约意向有路径影响。
2.模型应用软件Amos计算时的假设条件[15]
如果满足以下的前提假设:线性关系(linearity of relationships),观察值独立(即甲样本的选取独立于乙样本的选取,换句话说就是,样本的选择随机的),观察值必须满足正态分布的要求,那么,Amos就会产生“渐进结论”(asymptotic conclusions),即获得的结论是“几乎正确”(approximately true)。
四、变量筛选与样本数据的处理及检验
(一)变量的选择
从理论上确定违约风险的可能影响因素主要依据以下3方面:一是充分借鉴国外以往研究的经验和类似研究的结果;二是结合国内实务界在实际操作中的直接经验;三是充分利用有限的样本数据。变量选择主要集中在如下3个特征:借款人特征、家庭财务负担和贷款特征。设借款人特征为F1,家庭财务负担 F2,贷款特征 F3,违约意向为F4。
(二)变量的量化
表1为变量量化的处理。处理后变量的数值类型,多数为离散型数据,部分为连续型数据。
(三)样本数据的处理
1.样本筛选 本文数据是以银行信贷系统中实际搜集调查而来,将已搜集到的多家商业银行2010年四季度住房贷款数据为备选样本。由于结构方程所处理的变量之间的关系较为复杂,因此为了维持统计假设不违反,必须使用较大的样本数。为得到稳定的结构方程分析结果,本文最终选取1.5万个样本为分析样本。

表1 变量的量化
2.缺失值处理 缺失值的存在,在很大程度上影响分析的结果,所以必须对缺失值进行处理。本文采取了表列删除法,即在一条记录中,只要存在一项缺失,则删除该记录。使用SPSS18.0进行操作处理,经过检验,本文选取的数据中有缺失值的共有2340个,将这部分有缺失值的样本删除,并基于剩下的12660个样本做异常值剔除分析。
3.异常值筛选 运行 AMOS18.0,计算每个观察值远离重心(centroid)的 Mahalanobis d_squared(Mahalanobis)距离,并以大小加以排序。输出结果中观察p1和p2值。当p2值很小时,即p2<0.05表示该观察值为异常值。经过筛选发现总体样本中有2590个异常值,将其剔除后,留下10070个符合建立结构方程要求的有效样本。
(四)样本数据信度检验
信度(reliability)指测量结果(数据)一致性或稳定性的程度。对于Cronbach Alpha值,当0.35≤Cronbach α <0.70 时,属于尚可;当 Cronbach α<0.35时则为低信度。基于以上限制条件,本文的数据均达到了有效地标准,为信度良好的数据。
五、结构方程模型的建立
(一)初始模型建立
根据所设计的基本路径假设,由此构造结构路径图,如图1。

图1 结构方程初始模型
在AMOS中,进行正态性检验,得出c.r.值为52.79,而当c.r.>2时则暗示有单变量具有异常值。当c.r.>1.96表示有些单变量违反正态分布的假设。若违反多变量正态分布的条件会导致高估及低估参数估计值的标准。同时在当数据满足正态分布时,偏度系数skew与峰度系数kurtosis均要接近于0,如果skew>3,kurtosis>8需要引起注意。在初始模型中,变量还款方式的两个参考系数偏度系数skew和峰度系数kurtosis分别为4.65>3,19.60>8,均超过了标准值。变量担保方式的峰度系数kurtosis分别为15.70也都大于标准值,因此,样本的2个变量均没有通过正态检验,在结构方程中,将此2个变量剔除。因此结构方程调整为图2。
(二)模型的拟合度分析
拟合度Model fit summary,对绝对拟合指数χ2,GFI,RMR,SRMR,RMSEA 等数值能说明模型的拟合度程度,实证结果见表2所示

图2 结构方程优化模型

表2 拟合度分析
CMIN是差异(discrepancy)的宏函数。差异表示卡方值(Chi-square)可以检查模型是否适合数据。当完全适合数据时,差异值为0。根据表2中数据,本文建立的模型的差异为68.546,说明该模型拟合度不好。P是指显著性。显著性大于0.05,即可认定该模型与数据拟合适度;当显著性小于0.05即可认定该模型与数据拟合不适度。表2中P值是0.000<0.05,可以判断模型不适合数据。RMR越接近0表示模型拟合度越好,通常采用RMR<0.05。表2中RMR=0.91表示配合不够理想。RMSEA是指平均平方误差平方根。可修正总体差异值受到估计参数值影响的缺点。RMSEA<0.05时,模型拟合度良好。RMSEA>0.1时,表示模型拟合度差,应调整模型。当0.05<RMSEA<0.1时,表示模型处于灰色地带,不满意但尚可接受。表2中RMSEA值是0.06,0.05<0.06<0.1,不是完美拟合,但还是在可接受的范围之内。因此模型不必做出相应调整。
通过上述对模型拟合指数的分析,可以判断图2中的结构方程模型拟合度指数有部分拟合度比较高,也有部分拟合度偏低。针对拟合度不佳的情况,下面对模型进行修正,修正指标为M.I.值,若将 e2与 e5关联,将使 Chi-square减少60.90。说明受教育程度与贷款期限的残差存在相关关系,关联e2和e5得到修正模型,见图3。
(三)模型修正
修正结构方程模型,主要通过卡方值、P值和RMSEA拟合指标的变化来体现(图3)。

图3 结构方程修正模型
修正模型的拟合度分析见表3所示。
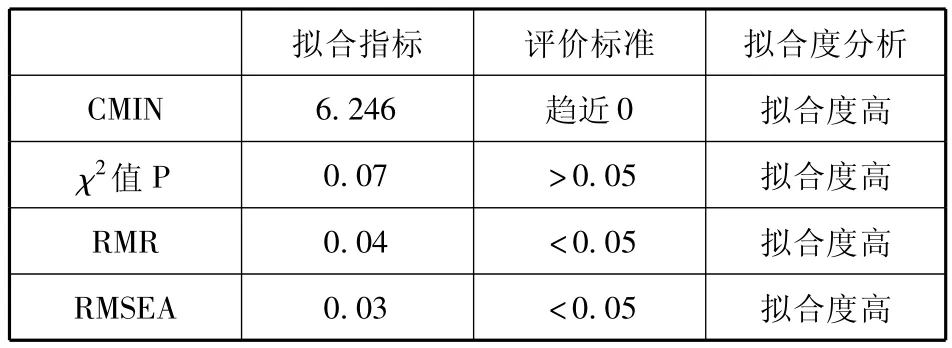
表3 拟合度分析
通过表3可以看出,拟合指数都得到了改善。该模型的各个参数在0.01的水平下都仍然是显著的,结构方程模型适配数据不仅拥有高拟合度,而且各方程对应的测定系数相对增大了。
(四)实证结果分析
从实证结果可以看出,3个潜变量贷款特征、借款人特征及家庭财务负担对个人住房抵押贷款的影响力度是逐渐减少的。同时测出与贷款特征相对应的显变量:贷款价值比、贷款期限、及还款方式、担保方式对贷款特征的影响力是逐渐减弱的;与借款人特征相对应得显变量:受教育程度、年龄、单位性质、职业和对借款人特征的影响是依次减少。针对上述分析结果可以从以下几个方面预防和控制个人住房贷款抵押贷款违约风险。
1.潜变量对个人住房抵押贷款违约影响的路径分析
在图3中,潜变量贷款特征、借款人特征与家庭财务负担对个人住房抵押贷款的影响是不同的。与借款人特征和家庭财务负担相比,贷款特征的影响力最大。通过结构方程的路径系数,可以很直观地判断出贷款特征具有更大的影响力,贷款特征对违约意向的路径系数为3.16,而借款人特征对违约意向的路径系数为2.46,家庭财务负担对违约意向的路径系数为1.86。此时,结构方程的拟合系数均达到了拟合度较高的程度。说明模型很吻合数据的要求,所测算出的结果很符合实际情况。
2.显变量对潜变量影响分析
潜变量贷款特征所对应的显变量有4个,分别是贷款价值比、贷款期限及还款方式、担保方式。对于还款方式、担保方式两个显变量,由于他们没有通过正态检验,并不能准确地反映对显变量贷款特征的影响力。而另外的两个变量贷款价值比、贷款期限,以高拟合度通过了正态检验。通过修正模型图3可得出,贷款价值比对贷款特征的路径系数为4.24;贷款期限对贷款特征的路径系数为1。因此可以看出,贷款价值比对于个人住房抵押贷款的违约有最直接的影响,也就是说,贷款价值比的多少会很大程度上影响借款人最终是否违约。
潜变量借款特征所对应的显变量有4个,分别是年龄、受教育程度、职业和单位性质。通过修正模型图3可得出,年龄对借款人特征的路径系数为1,受教育程度对借款人特征的路径系数为3.5,职业对借款人特征的路径系数为0.75,单位性质对借款人特征的路径系数为0.56,从结构方程的最终的结构图可以看出,受教育程度对于借款人是否会选择违约的影响最大。而借款人的年龄在一定程度上也会影响其选择违约。而职业和单位性质对于借款人来说影响很小,不是其选择违约的影响因素之一。
潜变量家庭财务负担所对应的显变量有3个,分别是月均收入、贷款金额和婚姻状况。图3可以看出,月均收入对潜变量家庭财务负担的路径系数为1,贷款金额对潜变量家庭财务负担的路径系数为3.56,婚姻状况对潜变量家庭财务负担的路径系数为0.66。说明贷款金额对家庭财务负担的影响最大。也就是说,贷款金额的多少会很大程度上影响借款人最终是否违约。针对实证结果,本文将提出减少我国个人住房抵押贷款违约的预防和控制措施。
六、结论与政策建议
贷款价值比的多少是影响借款人是否会选择违约的主要影响因素。银行在对借款人进行审批的过程中,对于贷款价值比比较低的借款人,应该采取谨慎的态度。避免造成不必要的损失。贷款期限对违约的影响力是有的,但是影响不大。对于贷款期限,当贷款期限长时,贷款后的每期还款压力相对较高,借款人违约的概率也高。银行应该采取相应措施控制借款人的贷款期限,以期减小风险。
我国商业银行在发放个人住房抵押贷款时特别应重视对下列指标的审核。受教育程度对借款人的影响往往是最大的。在实证研究的结果中可以看出,受教育程度的影响系数为3.5,说明受教育程度越高的人越不容易选择违约。在确信借款人诚实的基础上,银行应对借款人未来创造收入能力的评价进行审核。年龄同样在借款人特征中占有的权重比较大。中年型购房群体的违约风险最低,银行对于年龄偏大或者偏小的顾客应更严格的审查。以避免其违约的风险。借款人职业在一定程度上反映出了借款人收入稳定性。职业对借款人的影响很小,收入越稳定,违约概率越低。银行对于借款人单位性质的考察可作为一个衡量指标,对于从事高风险行业的借款人,工作单位相对缺乏稳定性,银行在进行审查市应加以控制。
贷款金额的多少是影响借款人是否会选择违约的主要影响因素。当贷款金额高,首付款低时,意味着借款人在该房产上的权益低,贷款后的每期还款压力也高,借款人违约的概率也较高。月均收入是影响家庭财务负担的主要因素,往往收入越稳定,违约概率越低,银行在发放个人住房抵押贷款时继续坚持对借款人收入来源及其稳定性的审查。婚姻状况对家庭财务负担的影响最小,其中已婚的购房群体的违约风险最低,是当前我国商业银行应积极发展的优质客户群。
[1]Roger Burrows.Mortgage Indebtedness in England:An‘epidemiology'[J].Housing Studies,1998(13):5 -23.
[2]Quercia,Roberto G,Michael A Stegman.Residential Mortgage Default[J].Journal of Housing Research,1992(3):341.
[3]刘春红.上海市个人住房抵押贷款违约因素实证分析[J]. 上海金融,2000(1):32-34.
[4]Lawrence,Edward C,Nasser Arshadi.A Multinomial Logit Analysis of Problem Loan Resolution Choices in Banking[J].Journal of Money,1995(27):202 -216.
[5]王福林,贾生华.个人住房贷款违约风险影响因素实证研究[J].经济学,2005:739-751.
[6]马 宇.中国个人住房抵押贷款提前偿付风险影响因素的实证研究[J].统计与信息论坛,2011:94-100.
[7]施锡锉,张 森.我国住房抵押贷款提前还款的博弈分析[J]. 财经研究,2002(10):35.
[8]Webb Bruce G.Borrower Risk under Alternative Mortgage Instruments[J].The Journal of Finanace.1998,37:169 -183.
[9]王震勤,王维才,李秋妍.个人住房抵押贷款风险防范机制分析[J].北京科技大学学报,2008:2
[10]Santos Silva J,J Murteira.Estimation of Default Probabilities Using in Complete Contracts Data[J].Univers Data Coimb,2000(7):22-27.
[11]汪利娜.北美、西欧的信用风险防范[J].中外房地产导报,2001(l):1-3.
[12]Nothaft,Frank E,Gcorge H K Wang.Modeling Dynamic Processes of Home Mortgage Delinquency and Foreclosure[J].Financial Management Association Annual Meeting,1993:125-345.
[13]刘 萍.个人住房抵押贷款风险探析[J].金融研究,2002(8):6.
[14]Arbuckle,James L.Amos 18.0 User's Gride[M].SC:Amos Develop Corporation,2010:1-120.
[15]吴明隆.结构方程模型-AMOS的操作与应用[M].重庆:重庆大学出版社,2009:8 -100.
Empirical Research on the Defaults Influence Factors upon Mortgage Loans for Existing Houses Based on Structural Equation Model
JIANG Ming - hui,CHEN Hao- jie,YUAN Tian - qi
(School of Management,Harbin Institute of Technology,Harbin150001,China)
Structural equation model(SEM)is used in defaults impact factors study on mortgage loans on existing houses.Compared with linearization method or logistic method which are used to study the relationship on default risk and impact factors(between latent variables and manifest variables),SEM increased path analysis between each manifest variable.Results,the main factors from model analysis are accurate and comprehensive.Policies relating prevention and control of the risks are proposed.
mortgage loans on existing houses;defaults;SEM model
F832
A
1002-9753(2012)01-0170-06
2011-08-26
2011-12-20
国家自然科学基金项目(HGQQ24601142)
姜明辉(1967-),男,黑龙江牡丹江人,哈尔滨工业大学管理学院教授,博士研究生导师,研究方向:商业银行风险管理。
(本文责编:海 洋)

