立式水轮发电机组导轴瓦间隙的计算研究

邓林森

(国电大渡河公司龚嘴水力发电总厂，四川乐山 614900)

1 概述

机组导轴承瓦隙计算是瓦隙调整的依据，是机组检修安装过程中的重要工作。瓦隙计算的准确度直接关系到瓦隙调整的质量，进而影响到机组运行中的振动、摆度、瓦温等安全稳定性指标。

瓦隙计算的基本要求在于通过适当的间隙分配，让同一部位导轴承的各块轴瓦分布在同一圆周上，同时确保各部位导轴承同心并且其中心连线与已经确定的理论旋转中心重合。瓦隙计算需要综合考虑设计瓦隙、轴系摆度、主轴位置等因素，计算过程中还会涉及到一些立体几何和三角函数等方面的知识，是一项较有技术含量同时也较为复杂的工作。

正是由于瓦隙计算的复杂性，同时由于部分技术人员对瓦隙计算准确度的重要性认识不足，在实际工作中，采取粗略计算甚至按经验估算的方式进行轴瓦间隙分配的做法仍普遍存在。若以这种间隙分配结果来指导瓦隙调整工作，往往会出现各部位导轴承不同心以及同一导轴承各导轴瓦不共圆的问题，进而影响机组的安全稳定运行。笔者以理论分析和实例计算相结合的方式，深入揭示了传统瓦隙计算存在的局限性，并系统介绍了一种更为精确的瓦隙计算方法。

2 摆度产生的原因及摆度公式推导

轴系产生摆度的原因是多方面的，主要包括轴线与镜板摩擦面不垂直、轴线与旋转中心线存在中心偏移或轴线本身曲折等因素。对于主轴某一具体测量部位而言，摆度产生的原因又可以直接归结于该部位主轴截面圆的圆心与其旋转中心不相重合这一因素。

首先建立一个简化的摆度测量模型:

在主轴圆周8等分的盘车系统中，假定机组旋转中心为O，某测量部位截面圆圆心的瞬时位置为O1，轴号位于轴上的点，此时方向百分表的读数为δA，当主轴旋转180°后主轴截面圆圆心的瞬时位置为O2，轴号将到达－Y轴上的A'点，轴号5'将到达+Y轴上的B点，此时+Y方向百分表的读数为δA与δB之差亦即线段AB的长即为该测量部位方位1～5'的摆度(图1)。

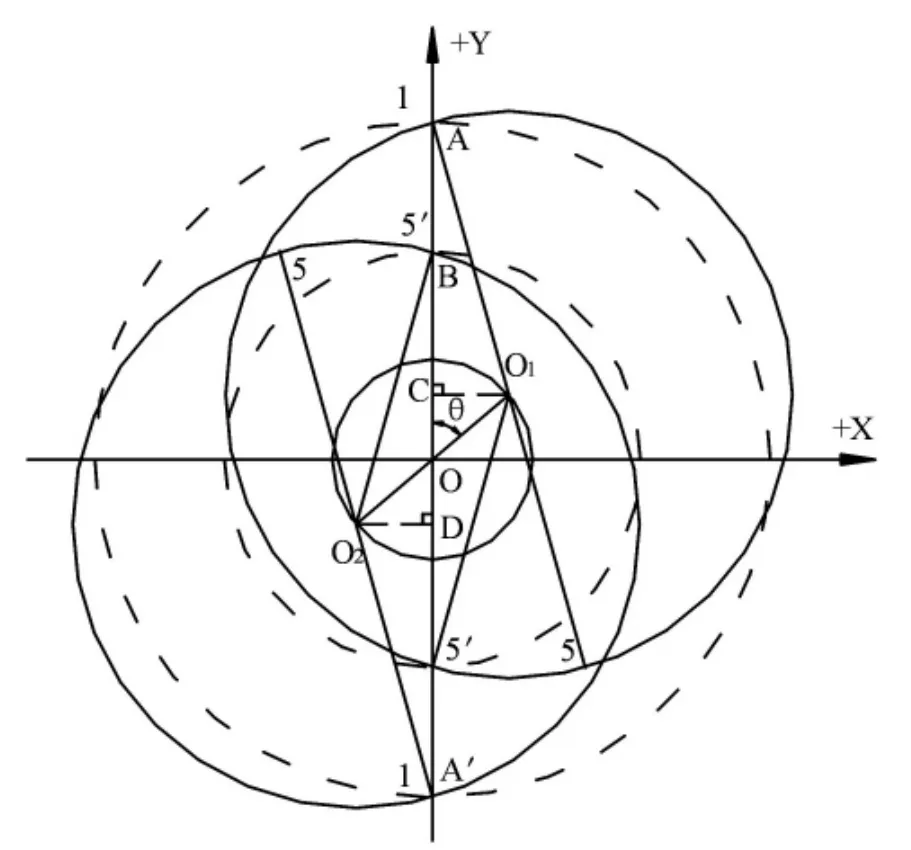
图1 摆度测量模型示意图

对上述模型进行数学分析如下:

分别过点O1和点O2向Y坐标轴作垂线，垂足分别为C和D;设 OO1=OO2=e，O1A=O2B=R，∠AOO1=θ，这里的e为主轴截面圆圆心相对于旋转中心的偏心距;R为主轴截面圆半径;θ为轴号与主轴截面圆圆心相对于旋转中心的方位夹角。

在△ACO1中:

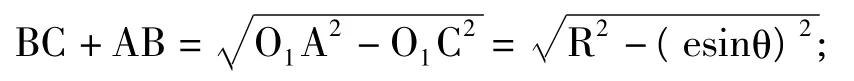
在△BDO2中:

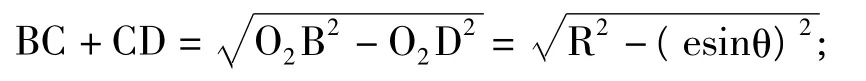
因此可得:AB=CD=2ecosθ。

推而广之，可得出摆度特性函数式:

φ(θ)=2esin(θ +90°)。

由此可见，旋转主轴的摆度特性遵循余弦或正弦规律;而且不难看出，对于主轴某一个测量部位而言，最大摆度只有一个，其大小为偏心距的2倍，方位与偏心方位一致。

3 盘车数据处理的理论分析及最大摆度公式推导

机组盘车的根本目的在于利用摆度特性规律并通过一系列技术手段找出最大摆度的大小和方位。在传统的盘车数据处理过程中，通常会引入净全摆度(将某测量部位某轴号的净摆度与直径方向对应轴号的净摆度之差称为该部位该直径方向上的净全摆度，同时把净全摆度等同于摆度公式中的摆度)这一概念，然后选取绝对值最大的净全摆度作为该测量部位的最大摆度，并以此作为瓦隙计算的基础。

事实上，盘车数据处理中的净全摆度概念为摆度特性规律的近似应用。这里仍然以图1中的摆度测量模型为例，摆度公式中的摆度为轴面上位于旋转中心两侧成180°的两点(轴号1及轴号5')经过同一百分表时的读数差;而盘车数据处理中的净全摆度为轴面上位于主轴截面圆直径方向的两点(轴号1及轴号5)经过同一百分表时的读数差。当且仅当轴号1位于旋转中心和主轴截面圆圆心连线的延长线上时，上述摆度测量模型中的轴号5与轴号5'才会完全重合，此时该方位的净全摆度才与摆度完全一致。在具体工程实践中，由于大轴轴径远大于偏心距，因此，既便在轴号5与轴号5'不重合的情况下，二者事实上也将极为接近。综上所述，我们认为这种将净全摆度等同于摆度公式中摆度的处理方式是可行的，它既能保证足够的精度，又能为数据处理带来便利。

如上所述，虽然将净全摆度等同于摆度公式中摆度的处理方式是可行的，但在主轴圆周8等分的典型盘车系统中，从盘车数据处理表格中仅有的4个净全摆度中选取绝对值最大的作为该测量部位最大摆度的做法其准确度往往是不够的。事实上，轴面上各轴号对应的测量点往往并不恰好位于最大摆度方位上，因此，传统的盘车数据处理方式往往不能获得旋转轴实际存在的最大摆度，这就需要借助摆度特性规律对盘车数据进行更为精确的处理。

下面利用摆度特性规律，阐述了简要推导实际最大摆度大小及方位的计算公式:

假定传统盘车数据处理得到最大净全摆度值为φ，次最大净全摆度值为φ，在主轴圆周8等分的盘车系统中，显然二者相角差为45°，而且实际最大摆度方位将位于最大净全摆度方位和次最大净全摆度方位之间。

假设实际最大摆度值为φ，则φ=2e;假设实际最大摆度与最大净全摆度相角差为β，则实际最大摆度与次最大净全摆度相角差为45°－β。

根据摆度特性规律，有:

由三角函数换算关系可以进一步推导出:

φ2=e(cosβ + sinβ)

反之，可以利用β值求出实际最大摆度值:

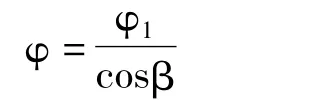
由此可见，实际最大摆度的大小和方位可以利用上述公式由最大净全摆度和次最大净全摆度精确地计算得出。

4 具体实例计算分析

某机组为半伞式结构，有上导、下导、水导三部导轴承，该机组大修过程中，轴线调整合格后的盘车数据及数据处理结果如表1所示。

从表1可以看出:上导最大净全摆度值φa1=0.19 mm(位于8号轴位)，次最大净全摆度值φc1=0.18 mm(位于7号轴位);水导最大净全摆度值φc1=0.24 mm(位于3号轴位)，次最大净全摆度值φc2=0.18 mm(位于4号轴位)。在粗略计算中，将以上述数据中的最大净全摆度作为上导和水导处的最大摆度，并以此为基础进行瓦隙计算。

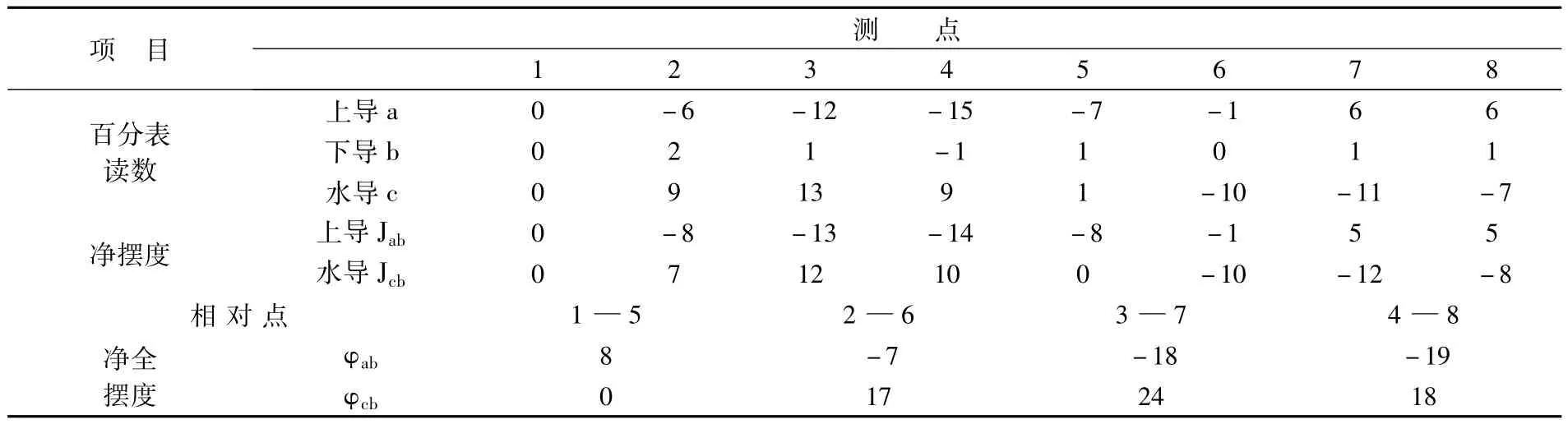
表1 盘车数据及数据处理表 /0.01 mm

根据前面推导的最大摆度公式可以计算得出:上导实际最大摆度方位位于7号和8号轴位之间且与7号轴位的夹角βa=18.8°，实际最大摆度值βa=0.2 mm;水导实际最大摆度方位位于3号和4号轴位之间且与3号轴位的夹角βc=3.5°，实际最大摆度值 βc=0.24 mm。在精确计算中，以此为基础进行瓦隙计算。

从以上实际最大摆度与最大净全摆度之间的偏差看，上导部位的偏差较大，而水导部位的偏差较小，该偏差实际上取决于最大净全摆度值和次最大净全摆度值之间的相对差值，具体来说是因为上导部位φa1与φa2之间的相对差值较小，而水导部位φc1与φc2之间的相对差值较大。

下面进一步交代瓦隙计算过程中将会涉及到的相关信息:该机组中心调整已结束，主轴位置已确定，下导轴承瓦隙按照设计间隙等隙调整;该机组上导瓦、水导瓦均为8块，其1号导轴瓦均位于+Y方向，其余导轴瓦按俯视顺时针依次编号，上导单侧设计瓦隙δa=0.2 mm，水导单侧设计瓦隙δc=0.25 mm;大轴上的盘车轴号按照俯视逆时针编号，盘车从轴号1位于+Y方向时开始，盘完一圈后轴号1回到+Y方向结束(图2)。

以下分别以两种不同的处理方式计算各上导轴瓦的间隙。

第一种方式，利用最大净全摆度进行粗略计算:

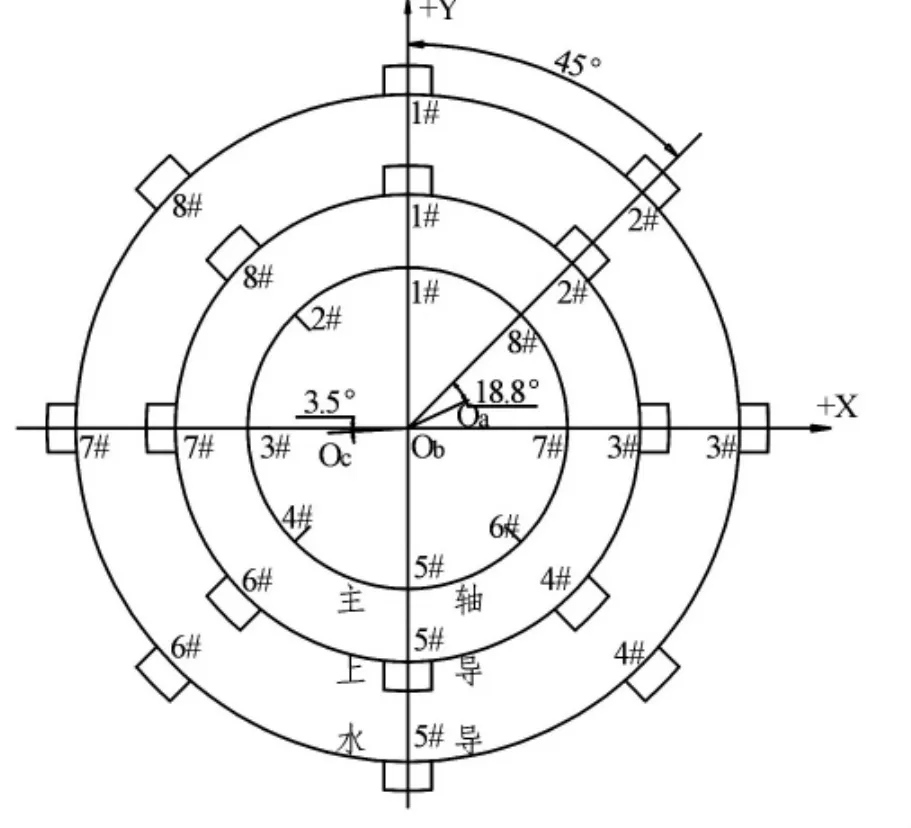
图2 导轴瓦及主轴位置示意图

第二种方式，利用实际最大摆度进行精确计算:

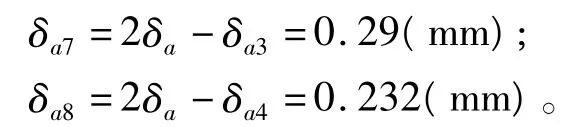
同理，亦可计算出水导轴瓦的间隙。上导、水导轴承两种瓦隙计算方式的最终结果见表2。

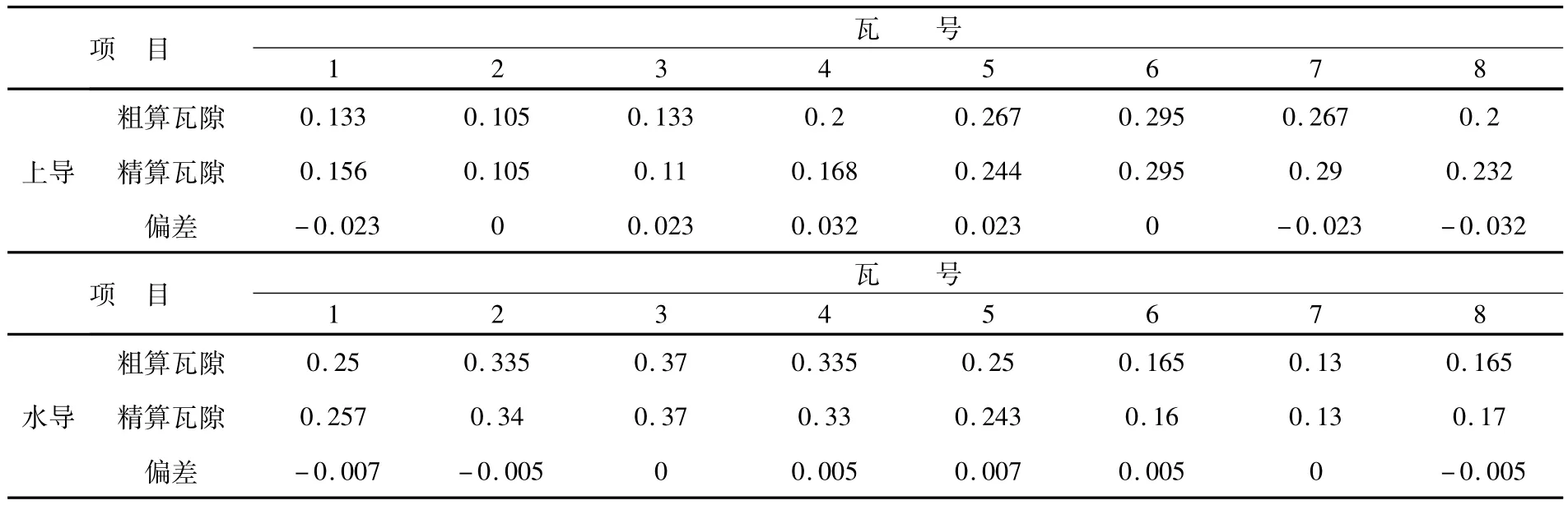
表2 粗略计算与精确计算结果对照表 /mm

由表2可以看出，两种不同处理方式计算得出的部分上导瓦隙偏差较大，最大达到0.032 mm。意味着若按照粗略计算的结果进行瓦隙调整，各上导轴瓦将不能准确地分布在以旋转中心为圆心的同一圆周上，势必导致各轴瓦受力不均，进而影响机组安全稳定运行。

同样由表2看出，两种不同处理方式计算出的水导瓦隙偏差较小，最大仅为0.007 mm。这种情况下，粗略计算的结果已基本能满足瓦隙调整需要，故可以不进行精确计算。

从瓦隙计算的过程中不难发现，两种不同处理方式存在的最大瓦隙偏差之所以有大有小，其根本原因在于各部位实际最大摆度与最大净全摆度之间存在不同的偏差。若这种偏差越大，则上述两种不同处理方式得出的瓦隙偏差将越大;若这种偏差越小，则上述两种不同处理方式得出的瓦隙偏差将越小。

5 结语

导轴瓦间隙计算的准确度从根本上取决于对该部位主轴最大摆度数据把握的准确度。瓦隙的精确计算就是建立在精确计算主轴最大摆度基础上的一种瓦隙计算方法，该方法与传统的粗略计算相比，虽然相对比较繁琐，但却可以显著提高各导轴瓦间隙分配的精确度。

鉴于瓦隙精确计算的工作量比较大，而且部分情况下粗略计算的结果也能满足要求，因此我们可以用次最大净全摆度值与最大净全摆度值之间比值的大小作为选择瓦隙计算方式的依据。一般来说，若该比值大于或等于0.8，就有必要进行瓦隙精确计算;若比值小于0.8，则进行传统的粗略计算即可。

［1］ 陈造奎.水力机组安装与检修［M］.北京:中国水利水电出版社，2002.