多重激子效应及其在先进太阳电池中的应用(下)

上海交通大学物理系凝聚态光谱与光电子物理实验室 上海交通大学太阳能研究所 苏未安 沈文忠

除多重激子产生的效率外，多重激子产生的阈值能量也是多重激子效应的一个重要参数。阈值能量ET[18,24,26,27,35,38]是指在纳米半导体中产生多重激子效应所需入射光子的最小能量h v'。从模型的建立可知，当产生多重激子效应时，IQE一定大于100%；并且多重激子产生效率依赖于参数tS、R和h v，IQE=IQE(tS, Eg, h v)。tS和Eg确定后，IQE仅取决于h v，则IQE=IQE(h v)。为便于计算，需给出纳米半导体中多重激子产生的判据IQE,cr(d,ET=h v')，即当IQE(d,h v)＞IQE,cr(d, ET=h v')时，产生多重激子效应；而IQE(d,h v)＜IQE,cr(d,ET=h v')时，不产生多重激子效应。IQE,cr(d, ET=h v')是一个大于100%且非常接近100%的一个数值。

也有一些科学家提出了相近方法以研究多重激子效应[50,51]，相比较而言，本文建立的模型改进的地方为:(1)考虑了电子自旋效应以及有效质量的影响，而其他方法[50,51]并未考虑电子自旋效应，且认为电子和空穴在纳米半导体中的运动质量等于电子的静止质量，这样的处理显然有欠妥当。(2)在本文模型中计算了光子能量驰豫体积Ω，而其他方法[50,51]则认为纳米半导体的体积V即为光子能量的驰豫体积Ω，因而，用统计模型所得结果的正确性更好。(3)结合碰撞电离机制和Fermi的统计模型，建立了适用于多重激子产生的统计模型，而其他方法[50,51]直接利用Fermi的统计公式计算多重激子的产生。尽管有的文献采用协同学理论讨论了多重激子产生过程[51]，但对于Fermi的统计公式是否适用于研究多重激子效应未作详细的分析。因而，正如后文将要表明的，前面所建的统计模型给出了与最近精细的实验数据[23,36]相符合的结果，而其近似的统计法得到了高达700%的多重激子产生效率[50,51]，这与现在的认识不符。

2 PbSe量子点中的多重激子效应

由于在纳米尺寸的材料中存在着量子限制效应，纳米半导体中的电子激发态变成为离散的电子态并且其带隙Eg(即HOMO-LUMO的跃迁能量)与其体积V有着非常紧密的关系[52～54]。对球形的量子点而言，V决定于其半径R，即V=4¹R3/3。1984年，Brus L E就根据量子力学的理论得到了著名的 Brus公式[53,54]:

式中:Eg0和ε分别为半导体材料的禁带宽度和介电常数；h为普朗克常数；e为电子的电量；式中第二项和第三项分别是附加的量子限制能量和库仑作用能量。

从式(7)可知，量子效应所附加的两项能量之间存在竞争关系，这种关系对量子点中多重激子效应产生影响，将在下文中详细讨论。而多重激子产生的特征时间参数tS，实验报道其值介于50～200 fS之间[37]。

Trinh M T 等人[23]第一次完全排除了多光子吸收和表面态等因素的影响，报道了Eg=0.65 eV的PbSe量子点吸收h v=3.1 eV的光子时，激子产率高达170%。为与Trinh M T 等人[23]的结果进行比较以验证统计模型的适用性，我们首先利用统计模型计算Eg=0.65eV的PbSe量子点中的多重激子产生效率。

根据Brus公式和PbSe材料的特性参数[55]，得到Eg=0.65 eV的PbSe量子点的半径R=3.90nm。由多重激子效应的统计模型，3.90nm的PbSe量子点吸收一个h v=3.1eV的光子时，在特征时间tS=50fs时，其产生1-，2-，3-和4-重激子的相对概率分别为 0.19321，0.77802， 2.87696×10−2和3.5593×10−7，多重激子产生效率IQE=183.6 %。该结果与Trinh M T等人[23]所报道的数据一致。因此，该统计模型可有效地预测纳米半导体中的多重激子产生。计算结果也表明特征时间tS的增加会导致多重激子效率IQE先增大然后趋于一个定值。当tS增大67.0fs时，IQE达到198.77%；此后，IQE几乎不变。可见，对于PbSe量子点，选择tS=50fs是合适的。

统计模型得到的结果表明在PbSe量子点中产生了多重激子效应，不仅因为IQE=183.6% ＞ 100%，非零值的n-激子(n=2, 3, 4)产生概率W(n)更是明确说明多重激子的出现。然而，由于相对概率W(3)和W(4)很小，“台阶状”的理想多重激子产生效率在实验上是不可能被观测到的，而报道的约高达700%的理想多重激子效应[24]，可能是因为没有排除多光子吸收及缺陷的阱效应这些“伪”多重激子产生而造成的结果。

现用统计模型来研究PbSe量子点中的多重激子效应，并根据数值计算的结果来探讨前面提到的文献[16,17,23,24,33,37,56]报道中关于多重激子产生效应的一些争议问题。

图1a给出了PbSe量子点吸收不同能量光子的多重激子效率IQE随其半径R的变化关系。由图可知，在tS=50fs时，多重激子效率IQE随着量子点半径R的增大先快速的增加，在半径R为16.20nm(图中虚线所示)时达到极大值；此后，随着半径的进一步增大IQE缓慢降低。计算的最大半径R达到了200 nm，是其激子玻尔半径[52,57](RB=36.6544 nm)的6.55倍，因而，激子在此PbSe量子点内的行为与在块材中一样。根据Yosuke Kayanuma的研究[58]，当PbSe量子点的半径R≤ 2RB=73.31 nm时，量子限制作用非常强烈；而当R≥RB=146.62 nm时，其量子限制作用微弱到可忽略。在半导体量子点中，库仑相互作用的增强也需考虑。半导体量子点的禁带宽度Eg由库仑相互作用和量子限制作用共同决定[见式(7)]。这两种作用之间的竞争关系，使得PbSe量子点的带隙Eg随着R的增大先急剧减小(图1b所示)，并在R为16.20nm(图1中虚线所示)处达到最小(Eg为0.24 eV)；而R＞16.20nm，Eg随着R的增大缓慢的增加。

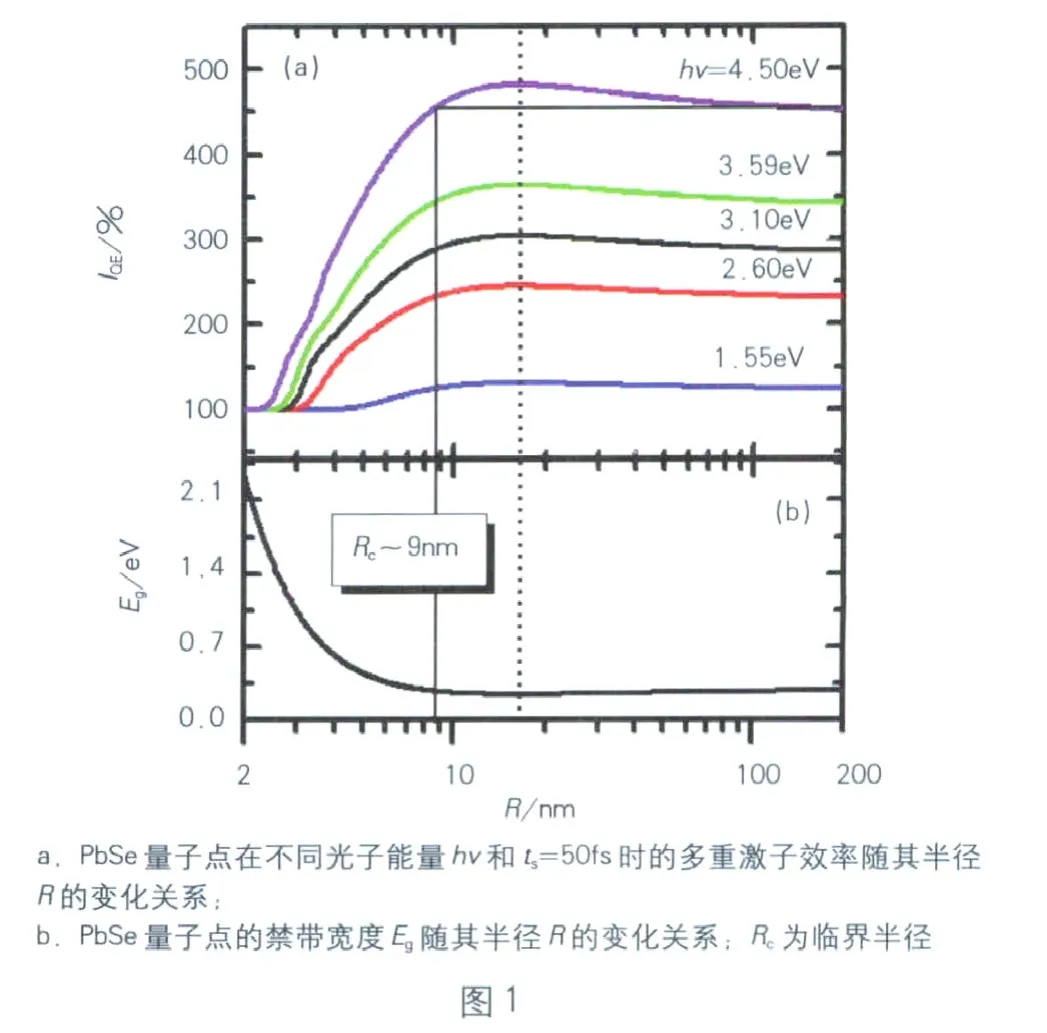
由图1a可知，当h v＞2Eg时，PbSe量子点多重激子效率IQE均大于100%。这表明在PbSe量子点中的确产生了多重激子效应。而多重激子效率IQE实际上是依赖于量子点半径R的一个函数关系式。当R ＜Rc时，其IQE小于PbSe块材半导体中的载流子倍增效率；而当R＞Rc时，量子点中的IQE大于PbSe中的载流子倍增效率。半导体PbSe量子点的临界半径Rc约为9nm。这一参数在制备高性能的光电器件方面将具有重要的价值。

图1a也表明随着入射光子能量的增加，PbSe量子点的多重激子效率IQE也随之增大。这一结果和前人的结果[16,17,23,24,33,37,56]一致。

文献对PbSe量子点的MEG阈值能量ET的报道分别为2.8eV[16]、5.1eV[18]和1.8eV[24]等，如图2a所示。此外，尽管能带结构计算[35]预示MEG归一化的阈值能量ET/Eg依赖于量子点的禁带宽度Eg，而大量的实验研究[16,18,21,22,24,25,37]却报道ET/Eg几乎与Eg没有关系，甚至有些小组认为ET/Eg仅是由材料决定的常数，可是对PbSe量子点的报道结论却不一致，ET/Eg为 3.0[16]和 2.1[17]。

图2a中的实线给出了以IQE,cr=101.0%为判据，tS=50fs所得到的PbSe量子点中多重激子产生的阈值能量ET，并以小方形的形式给出了文献中报道的结果。由图可见，阈值能量ET精密的依赖于PbSe量子点的半径R。随着R的增加，ET快速降低，在R=16.20nm时达到其最小值0.95eV，此后几乎不变。这样的变化趋势与图1b中R对Eg的影响一致。统计模型给出的阈值能量和文献报道的实验数据[16,18,21,22,24,25,37]都符合的很好。这样的结果表明，多重激子效应的阈值能量ET和量子点的尺度有紧密关系，或者说，ET和量子点的带隙Eg是有关系的。这样的结果与能带结构的计算结果[35]相一致。

图2b给出了多重激子效应的归一化阈值能量ET/Eg随量子点带隙Eg的变化趋势。尽管ET/Eg不是一个常数值，但当量子点的带隙大于Egc(1.04eV，图中以点线标出)后其值近似为常数ET/Eg为2.3。对于大尺度的量子点(Eg＜Egc)，ET/Eg依赖于其带隙Eg。而对于小尺度的量子点(Eg＞Egc)，ET/Eg几乎不随Eg的增加而改变，这和图2c中的箭头所示带隙范围内的报道结果[16,18,21,22,24,25,37]相一致。PbSe量子点中的多重激子产生阈值能量ET出现这种近似不变的趋势是由于带隙的增加与量子点尺度减小相互补偿的结果。

三 纳米硅半导体中的多重激子效应

1 纳米硅半导体的禁带宽度

尽管已有大量实验[59～62]和理论研究[45,62～65]以澄清纳米硅晶体中的量子限制效应，但到目前为止对于纳米硅的带隙Eg决定于其纳米硅直径的具体公式形式仍没有统一的结果。出现这种情况可能是由于样品的差异以及样品的复杂性所致。为进一步研究纳米硅半导体中的多重激子现象及其在光电子器件上的应用，依赖尺度的带隙Eg表达式就显得非常重要。通过拟合所报道的实验和理论数据[45,59～65](如图3所示)，得到描述纳米硅中带隙Eg(eV)和直径d(nm)之间的经验公式。该关系式表示为:

式中:第一项是晶体硅的带隙，拟合值1.15eV与文献报道的数据[55,66]非常符合；第二项说明Eg受电子和空穴的空间局域限制作用遵从d-1.36的变化关系，这一结果与文献所报道的d-1.39关系式[64]和d-1.37关系式[65]完全符合；第三项给出Eg依赖于尺度的库仑相互作用，随纳米尺寸的变化关系为d-1。

图3中的实线是采用拟合所得的公式所计算得出的硅量子点的带隙Eg随其直径的变化关系。很显然，该计算结果和大多数的实验及理论数据相符合。

2 纳米硅半导体中的多重激子效应

利用前面所建立的统计模型计算平均直径为3.8nm和9.5nm的硅量子点中的多重激子效率，以便于和下述文献所报道的在纳米硅半导体中测量的多重激子效率直接进行对比。文献报道的硅量子点直径呈现对数正态分布[26]。为进行有效对比，对硅量子点的尺寸分布按照标准误差为15%的对数正态分布进行理论计算。计算中的物理常数使用标准常数[67]，而Si中电子和空穴的有效质量分别为 m*n=0.19me和 m*p=0.286me[66]。

图4给出了在不同特征时间tS的理论计算得到的多重激子效率IQE随归一化的光子能量EP/Eg的变化关系，并给出了文献的实验数据[26]。从图4可以看出，在tS=50fs时，对3.8nm(红色实线)和9.5nm(黑色实线)的Si量子点计算的IQE和文献上的数据一致。然而，9.5nm的Si量子点在EP＞3.3Eg时的IQE低于报道的数据，这表明模型中的参数需进一步优化调整。

特征时间tS描述了入射光子的能量驰豫到量子点中所用时间，因而，它应该依赖于入射光子的能量EP。对吸收一定光子能量(EP=5Eg)的Si量子点进行了计算，其结果表明大量子点(d＞6.0nm)的多重激子效率IQE强烈的依赖于tS，小量子点(d＜6.0nm)的IQE几乎不随ts变化。因而，再次计算tS=150fs时Si量子点中的多重激子效应。结果显示，3.8nm的Si量子点中多重激子效率与tS=50fs时该量子点中的IQE一样(图4中红色短线和红色实线重合)；而9.5nm的Si量子点中的IQE与报道的数据高能部分符合的较好，但在低能部分的差异很大(图4中的黑色短线)。这再次揭示出tS应依赖于入射光子的能量EP。

半导体量子点中的热电子冷却与多重激子效应具有相似的物理过程[15,68]，而前者的驰豫时间和电子能级间距值之间满足幂指数的函数关系[68]。因此，假定多重激子产生的特征时间tS与归一化的入射光子能量值EP/Eg之间也满足幂指数函数关系:tS(EP/Eg)=35.0+3.0×10−9exp[21.0(EP/Eg)1/10]fs。计算结果表明，当多重激子产生的特征时间取tS(EP/Eg)时，3.8nm和9.5nm的Si量子点中多重激子产生效率IQE与文献所报道的数据均较好的符合(见图4中的红色虚线和黑色虚线)。这表明，采用tS=tS(EP/Eg)参数时，前面建立的统计模型仍能适用于Si量子点中多重激子效应。

现在，我们利用已建立的统计模型[参数tS=tS(EP/Eg)]来探讨Si量子点中的多重激子效率IQE。图5给出了计算的Si量子点中多重激子效率IQE对量子点直径d(=2R)和归一化入射光子能量EP/Eg的依赖关系。结果表明，当Si量子点的尺度确定时，其内的多重激子效率在低能入射光子时几乎保持不变，而在高能光子入射时随能量的升高而增加。这一结果与报道的情况一致[16～18,23,24,36,37,39]。

图5的多重激子效率有“台阶”状的变化特征，这样的变化在图2中也存在。多重激子效率曲线中的“台阶”正对应于IQE为整数，这说明“台阶”状的出现是由于吸收一个光子只能产生整数个电子—空穴对的缘故。对于较高能量的光子入射，在理论上[24,34]和实验上[10,47]都报道了“台阶”状的多重激子效率，并认为这种“台阶”是最具特征的多重激子产生图谱[47]。

另一方面，由图5可知，当EP/Eg一定时，Si量子点中多重激子效率IQE随其尺寸的增大先急剧增大，然后几乎不变。Si的激子玻尔半径aB=4.9nm，计算的量子点尺寸均小于3aB，故其内的量子限制效应不可忽略。量子点中的库仑相互作用增强使多重激子效率增大[16,31]； 而空间局域限制使得能态密度降低，从而导致其中的多重激子效率减小[33]。小量子点中局域限制作用强于库仑相互作用的增强，因而，小尺度的Si量子点中的多重激子效率IQE随尺寸的增大快速增加。

图5中灰带是以IQE,cr=101.0%为判据所计算得到的Si量子点中多重激子产生的阈值能量ET。结果表明，ET依赖于Si量子点的尺寸:当直径d由1.0nm增加到5.2nm时, ET从3.1Eg降到2.2Eg；此后，ET随着d的增大只缓慢的上升。理论计算得到的依赖于Si量子点大小的阈值能量ET为3.1Eg到2.2Eg。9.5nm的Si量子点ET为2.3Eg，这和文献报道 2.4±0.1Eg[26]的结果一致。

3 纳米硅中多重激子效应的应用

现在，我们进一步探讨纳米Si中多重激子效应在光电子器件上的可能应用，尤其是在太阳电池和高灵敏的探测器器件上的潜在应用价值。

利用半导体量子点的多重激子效应改进了细致平衡模型以计算单结Si量子点太阳电池的能量转换效率。图6a给出了对工作温度300K的单结Si量子点太阳电池在AM1.5G太阳光谱照射的计算结果。可见，Si量子点太阳电池的转换效率随着Si量子点直径d的增大先升高，这种变化趋势是由于禁带宽度Eg造成的；只有在较大Si量子点(d＞5.0 nm)制备的单结量子点太阳电池中，多重激子效应才能增强其能量转换效率，理想的多重激子效应最大能够将转换效率提高5%，而由统计模型给出的多重激子效率最好仅能将太阳电池效率能提升1%。太阳电池的能量转换效率是由太阳光谱与量子效率变化曲线的重叠决定。而较大的禁带宽度(Eg＞1.15eV)及较高的阈值能量(ET为2.2Eg～3.1Eg)使得Si量子点的内量子效率曲线和AM1.5G太阳光谱的重叠区域变小，从而导致多重激子效应对单结Si量子点太阳电池能量转换效率的增强作用是有限的。

尽管Si量子点中多重激子效应在量子点太阳电池上的实际应用受限，但量子点中的多重激子效应对染料敏化电池性能的提高是巨大的[7]。此外，但Si量子点吸收150nm光波时，其内量子效率高达490%(图6b)，这说明多重激子效应在提高紫外探测器的性能方面具有重大的潜在价值，这样的潜在价值已初步为实验所证实[69]。

四 结语

以半导体量子点中多重激子产生的电离碰撞机制为基础，结合Fermi建立的处理多个基本粒子产生的统计方法，建立了一个能够在较大尺寸范围内处理半导体量子点中多重激子效应的简单而有效的统计模型。并使用该模型对PbSe量子点中的多重激子效应进行了探讨，结果表明该统计模型可以很好地解释PbSe中的多重激子效应，包括多重激子产生的效率和多重激子的阈值能量。这个简单而有效的模型可统一几乎所有的量子点中多重激子效应的争议。模型的计算结果表明PbSe量子点中的确存在多重激子效应，并且存在一个临界半径Rc，当量子点半径R＜Rc时，其内的多重激子产生效率低于PbSe半导体中的载流子倍增效率，而当R＞Rc时，量子点内的多重激子产生效率高于PbSe半导体中的载流子倍增效率。此外，多重激子效应的阈值能量是量子点尺度的函数，和目前文献报道的结果一致。

利用统计模型，并结合Si量子点禁带宽度Eg(d)的经验公式，详细探讨半导体Si量子点中的多重激子产生效应。并根据改进的细致平衡理论模型，探讨了Si量子点中多重激子产生对于单结Si量子点太阳电池的能量转换效率的增强效果。结果表明，理想多重激子产生能够将能量转换效率提高5%，而统计模型计算的多重激子产生能提升1%。

在应用上，多重激子效应对于染料敏化电池性能提高的具有重大的潜在价值。此外，短波光照下的很高的内量子效率(在150nm的光照时，其最大内量子效率可达490%)给多激子产生效应紫外探测器上的应用也展示出了美好的前景。

[50]Oksengendler B, Turaeva N, Rashidova S. Statistical theory of multiple exciton generation in quantum dot solar cells[J]. Applications of solar energy, 2009, 45 (3): 162－165.

[51]Turaeva N, Oksengendler B, Uralov I. Synergetics in multiple exciton generation effect in quantum dots[J]. Applied Physics Letters,2011, 98 (24): 243103.

[52]Yoffe A D. Low-dimensional systems: quantum size effects and electronic properties of semiconductor microcrystallites (zero-dimensional systems)and some quasi-two-dimensional systems[J].Advances in Physics, 1993, 42 (2): 173 － 262.

[53]Brus L. Zero-dimensional "excitons" in semiconductor clusters[J]ournal of IEEE Journal of. Quantum Electrons, 1986, 22 (9): 1909－1914.

[54]Brus L E. Electron-electron and electron-hole interactions in small semiconductor crystallites: The size dependence of the lowest excited electronic state[J]. The Journal of Chemical Physics, 1984, 80(9): 4403－4409.

[55]Madelung O. Semiconductors: data handbook[M]. Springer Verlag, 2004.

[56]Moreels I, Lambert K, De Muynck D, et al. Composition and size-dependent extinction coefficient of colloidal PbSe quantum dots[J]. Chemistry of Materials, 2007, 19 (25): 6101－6106.

[57]Kayanuma Y. Wannier exciton in microcrystals[J]. Solid State Commun ications, 1986, 59 (6): 405－408.

[58]Kayanuma Y. Quantum-size effects of interacting electrons and holes in semiconductor microcrystals with spherical shape[J]. Physical Review B, 1988, 38 (14): 9797－9805.

[59]von Behren J, van Buuren T, Zacharias M, et al. Quantum confinement in nanoscale silicon: The correlation of size with bandgap and luminescence[J]. Solid State Communications, 1998, 105 (5):317－322.

[60]Furukawa S, Miyasato T. Quantum size effects on the optical band gap of microcrystalline Si:H[J]. Physical Review B, 1988, 38(8): 5726－5729.

[61]Kim T Y, Park N M, Kim K H, et al. Quantum confinement effect of silicon nanocrystals in situ grown in silicon nitride films[J].Applied Physics Letters, 2004, 85: 5355.

[62]Van B T, Dinh L, Chase L, et al. Changes in the electronic properties of Si nanocrystals as a function of particle size[J]. Physical Review Letters, 1998, 80 (17): 3803－3806.

[63]Zhang Q, Bayliss S. The correlation of dimensionality with emitted wavelength and ordering of freshly produced porous silicon[J]. Journal of Applied Physics, 1996, 79 (3): 1351－1356.

[64]Proot J, Delerue C, Allan G. Electronic structure and optical properties of silicon crystallites: Application to porous silicon[J].Applied Physics Letters, 1992, 61 (16): 1948－1950.

[65]Wang L W, Zunger A. Electronic structure pseudopotential calculations of large (～1000 atoms)Si quantum dots[J]. The Journal of Physical Chemistry, 1994, 98 (8): 2158－2165.

[66]Chen X, Zhao J, Wang G, et al. The effect of size distributions of Si nanoclusters on photoluminescence from ensembles of Si nanoclusters[J]. Physics Letters A, 1996, 212 (5): 285－289.

[67]Mohr P, Taylor B, Newell D. CODATA recommended values of the fundamental physical constants: 2006[J]. Reviews of Modern Physics, 2008, 80 (2): 633－730.

[68]Kr‡l K, Hot-electron cooling and hot-phonon generation with collision broadening[J]. Physical Review B, 1994, 50 (11): 7988－7991.

[69]Generation M. Colloidal quantum-dot photodetectors exploiting multiexciton generation[J]. Science, 2009, 324: 1542－1544.