BP小波神经网络在边坡位移预测中的应用
李方,闫永慧
(江苏省南京工程高等职业学校,江苏南京211135)
BP小波神经网络在边坡位移预测中的应用
李方,闫永慧
(江苏省南京工程高等职业学校,江苏南京211135)
用优化的BP小波神经网络建立的预测模型对吊钟坝边坡的变形量进行了预测。引入了共轭梯度反向传播算法来优化BP小波神经网络,从而使网络计算量大为减少,避免了网络产生局部最优的弊端,有效提高了网络的质量。与未优化的BP小波神经网络和BP神经网络的预测结果进行比较可以看出,优化的BP小波神经网络的预测值更接近GPS实测值。
位移预测;优化BP小波神经网络;边坡;重庆忠县
0 引言
边坡是岩石圈表面受天然地质和工程地质的作用,具有侧向临空面的地质体。其形成和演变过程与人类生产、生活密切相关。随着人口的急速增长和土地资源的过度开发,诸如当前人们广为知晓的危岩、滑坡、泥石流一类的边坡灾害己演变成同地震、火山相并列的全球性三大地质灾害(源)之一。因此,有关边坡位移的预测已成为比以往任何时候都更加重要、更为迫切的研究课题。
边坡位移是边坡岩土体在开挖或变形过程中反馈出的重要信息之一。利用实测边坡位移序列来预测边坡未来时间的位移,从而为判断边坡的稳定性提供必要的依据。目前,常用的边坡位移预测方法主要有以下几种:灰色系统理论预测法(赵静波等,2005)、时间分析建模预测法(宋克志,2004)、人工神经网络预测法(宋克志等,2003;沈强等,2006;张正禄等,2010)。由于边坡位移时间变化表现出很强的非线性特征,从而使边坡位移系统成为一个复杂的非线性动力学系统。在以上提及的3种方法中,人工神经网络预测法在解决非线性问题方面更为突出。所以,比较而言,研究人工神经网络方法预测边坡位移更有意义。笔者应用属于神经网络范畴的BP小波神经网络并对其进行优化后来预测边坡位移,与未优化的BP小波神经网络(BP-WNN)和BP神经网络(BP-ANN)相比,预测效果明显。
1 BP小波神经网络原理及其模型
1.1 优化的BP小波神经网络原理
小波神经网络由法国著名的信息科学研究机构IRISA的Zhang Qinhua等(1992)提出,是用小波函数去代替前向神经网络激活函数(Sigmoid函数)。BP小波神经网络则是用小波函数去代替BP神经网络的激活函数。
BP神经网络(吴益平等,2005;韩力群,2006)属于前向神经网。它的学习过程是由信号的正向传播与误差的反向传播两个过程组成。正向传播时,输入样本从输入层传入,经各隐含层逐层处理后,传向输出层。若输出层的实际输出与期望的输出不符,转入误差的反向传播阶段。误差的反向传播是将输出误差以某种形式通过隐含层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程,是周而复始进行的。权值不断调整的过程,也就是网络的学习训练过程。此过程一直进行到网络输出的误差减小到可接受的程度,或进行到预先设定的学习次数为止。
单隐含层单输入单输出的BP小波神经网络(Daif et al,2001;Shi et al,1998)的结构如图1所示。x为输入样本,ψk(k=1,2,…,l)为小波函数,y为网络输出。同时用ωk表示网络输出y与隐含层第k个神经元间的连接权值。

图1 BP小波神经网络结构示意图
对于连续参数的BP小波神经网络,ψk=,其中,ψ为小波函数,ak、bk分别为该小波函数的尺度参数和平移参数,此时神经网络的输出y可表示为:

网络输出y与原始数据Y之间的误差大小取决于网络参数ωk、ak和bk。其中,参数ωk、ak和bk可以通过下面最小均方误差能量函数E进行网络优化,这就是BP算法所采用的梯度下降法减小误差函数的方法。

式(1)中,采用Morlet小波函数,其表达式如下所示:



为了便于控制训练效果,每次循环之后的网络输出误差用相对误差表示:

笔者采用了一种新的参数优化方法,即共轭梯度反向传播算法(牛东晓等,1999),使BP小波神经网络计算量大为减少,避免了产生局部最优的弊端,有效地提高了网络的质量。
优化网络参数ωk、ak和bk,分别令向量ω= (ω1,ω2,…,ωk,…,ωl),g(ω)=(g(ω1),g(ω2),…,g(ωk),…,g(ωl)),s(ω)i为ω的函数的第i次

权重向量按下式进行调节:

在此采用一维搜索变步长法计算最佳步长αi
ω。每次循环时,按式(8)、式(9)分别调节网络参数向量ω,直至收敛于某一确定值或循环结束为止。对于参数ak和bk的优化同样按上述方法进行。
1.2 优化的BP小波神经网络模型
BP小波神经网络是单输入单输出网络,其输入样本为边坡位移实测的时间序列x,输出样本为边坡位移的实测值Y。根据经验公式(l为隐含层神经元数;m=1,为输入层神经元数; n=1,为输出层神经元数;p为1~10之间的常数),并且进行多次试验,确定隐含层神经元数的个数为8。
模型训练步骤为:(1)初始化网络参数ωk、ak和bk,并且随机生产,设置网络的学习率η和允许误差ε;(2)输入学习样本x和输出样本Y;(3)计算网络的实际输出y;(4)用共轭梯度反向传播算法优化网络参数ωk、ak和bk;(5)误差计算,用式(7),当其小于允许误差ε或者达到最大指定迭代次数时,网络学习过程结束。否则,网络进行误差反向传播,使E=0,返回式(2),重新开始网络计算。
2 吊钟坝边坡位移预测研究
2.1 吊钟坝边坡概况
吊钟坝边坡位于重庆市忠县西南约18 km的望水乡钟坝河左右两岸坡上,左岸(钟坝村滑坡)隶属望水乡钟坝村,右岸(中华村滑坡)隶属望水乡中华村。吊钟坝滑坡紧临望水乡,有两条道路与忠县相连,公路里程约为20~25 km。
因该边坡面积较大,通视困难,在2006年9月29日,通过使用GPS方法进行平面和垂直位移观测,每半个月进行1次监测。根据已有勘察、监测资料分析,在边坡变形体位移变形较大处布设了12个位移变形监测点,编号为J1—J12。笔者选用的是监测点J7—71,2007年11月15日—2008年10月30日的水平位移(ΔH/mm)和垂直位移(ΔS/mm)的变形量。
2.2 优化的BP小波神经网络边坡位移的预测
选取2007年11月15日—2008年05月30日的水平位移(ΔH/mm)和垂直位移(ΔS/mm)的变形量分别14组。
进行参数优化的BP小波神经网络的学习,对2008年06月15日—2008年10月30日的水平位移和垂直位移的变形量各10组分别进行预测,结果如表1、表2所示。
参数优化的BP小波神经网络与BP神经网络和未优化的BP小波神经网络的预测结果比较,在相同的训练次数下,参数优化的BP小波神经网络预测结果更接近GPS实测值。
由图2、图3可以看出,优化的BP小波神经网络拟合值曲线与GPS实测值曲线几乎重合,说明优化的BP-WNN方法能够很好地预测边坡位移的变形量。
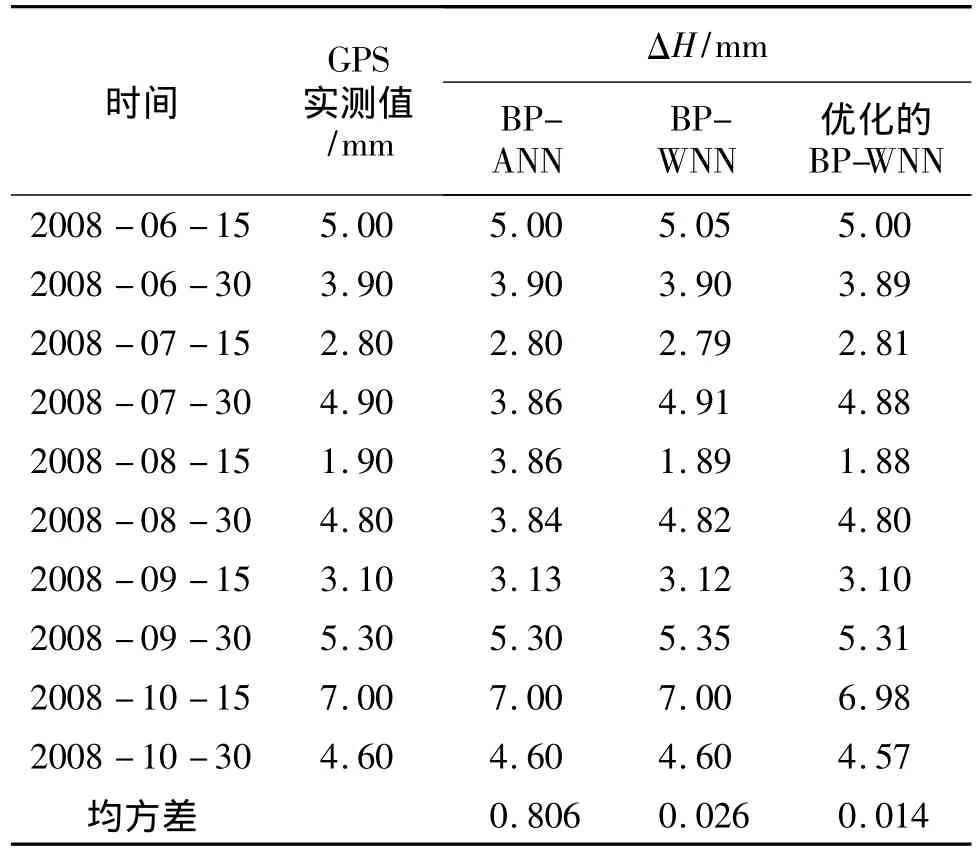
表1 水平位移的3种预测方法的比较
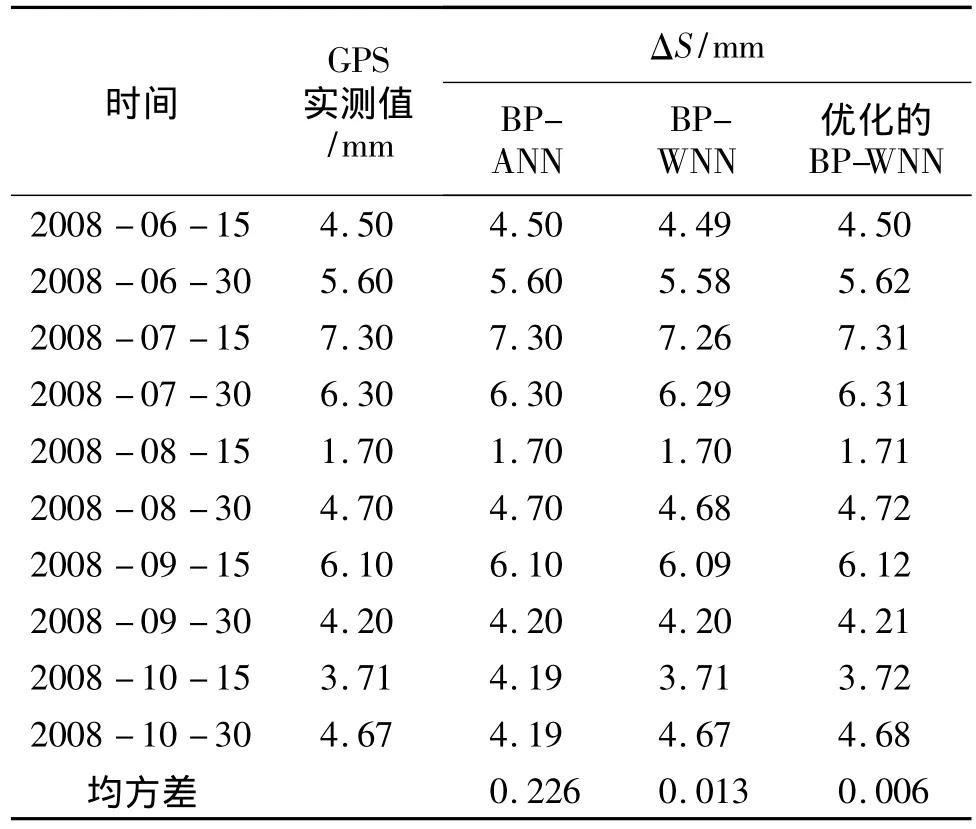
表2 垂直位移的3种预测方法的比较

图2 水平位移实测值与拟合值曲线图

图3 垂直位移实测值与拟合值曲线图
3 结论
引入了共轭梯度反向传播算法来优化BP小波神经网络,从而使网络计算量大为减少,避免了网络产生局部最优的弊端,有效提高了网络的质量。通过对BP小波神经网络的优化,建立了边坡位移的预测模型。
用优化的BP小波神经网络建立的预测模型对吊钟坝边坡的水平位移和垂直位移的变形量进行了预测,其结果与未优化的BP小波神经网络和BP神经网络的预测结果进行比较。可以看出,优化的BP小波神经网络的预测值更接近GPS实测值。通过更加准确地预测边坡位移的变形量,可以避免边坡稳定性分析计算方法的冗长繁琐和不确定性,并且可以为控制位移变形量及采取相应的工程措施提供有价值的参考。
韩力群.2006.人工神经网络教程[M].北京:北京邮电大学出版社.
李金屏,王风涛,杨波.2001.BP小波神经网络快速学习算法研究[J].系统工程与电子技术,23(8):72-75.
牛东晓,邢棉.1999.时间序列的小波神经网络预测模型的研究[J].系统工程理论与实践,19(5):89-92.
宋克志,王梦恕,宋克勇.2003.边坡位移预测的神经网络模型研究[J].岩石力学与工程学报,(增刊1):2382-2385.
宋克志.2004.边坡位移时间关系模拟的人工神经网络模型[J].煤炭学报,29(4):405-408.
沈强,陈从新,汪稔.2006.边坡位移预测的RBF神经网络方法[J].岩石力学与工程学报,(增刊1):2882-2887.
吴益平,唐辉明,葛修润.2005.BP模型在区域滑坡灾害风险预测中的应用[J].岩土力学,26(9):1409-1413.
赵静波,李莉,高谦.2005.边坡变形预测的灰色理论研究与应用[J].岩石力学与工程学报,24(A02):5799-5802.
张正禄,王小敏,邓勇,等.2010.模糊神经网络在变形分析与预报中的应用研究[J].武汉大学学报:信息科学版,(1):6-8.
DAIF C,LEE C F.2001.Frequency-volume relation and prediction of rainfall-induced landslides[J].Journal of Engineering Geology,59(3/4):253-266.
SHI JING SHENG,ORTIGAO J A R,BAI JUNLI.1998.Modular neutral networks for predicting settlements during tunneling[J].Journal of Geotechnical and Geoenvironmental Engineering,124(5):389-395.
ZHANG QIN HUA.1992.Wavelet networks[J].IEEE transactions neural networks,3(6):889-898.
Application of BP wavelet neural-network in prediction of slope displacement
LI Fang,YAN Yong-hui
(Jiangsu Nanjing Engineering Vocational College,Nanjing 211135,China)
Based on the engineering fact of Diaozhongba slope,an optimization method of BP wavelet neural-network was used to predict displacement of slope.The method used conjugate gradient back propagation algorithm optimizing BP-WNN parameters,reduced large amount of network calculation volume,avoided the drawbacks of local optimum result and improved the quality of the network.Compared with non-optimized BP wavelet neural-network,the predicted values measured by the optimized BP wavelet neural-network were more close to those measured by GPS.
Displacement prediction;Optimized BP wavelet neural-network;Slope;Zhongxian County,Chongqing
book=2,ebook=56
P542+.31
A
1674-3636(2012)02-0134-04
10.3969/j.issn.1674-3636.2012.02.134
2011-05-24;
2011-05-30;编辑:陆李萍
李方(1982—),女,讲师,硕士,地球探测与信息技术专业,现从事岩土工程勘察方面的研究,E-mail:jimodefox@163.com

