对两个频率相近成分作频谱校正的非迭代形式研究

张 强，张 频，陈奎孚

(1.上海师范大学 建筑工程学院，上海 201418；2.江西农业大学 国土资源与环境学院，南昌 330045；3.中国农业大学 理学院，北京 100083)

对于非密集频率复杂谐波信号，基于复正弦模型(Complex Sinusoid Model：CSM)的校正技术已经发展得几近完美［1－6］，有关的综述参考文献［7－8］。该方法仅仅利用主瓣附近几条的离散谱线数据，经过简单运算就可以得到相当精确的参数。对于频率密集模型，是否还存在这种不需迭代的校正技术，尚未见文献给出明确答案。最简单的频率密集模型是双频率模型(Double-Frequency Model：DFM)。针对这种模型，文献［9］通过搜索两个频率分量在复平面上的方位角将其分离，它需要使用数值法搜索。文献［9－10］直接用数值方法迭代求解非线性频率方程，因而两者算法复杂性和运算量都远远超出CSM的简单校正方法。

本文将探索对于DFM，是否存在类似CSM的显式校正公式。本文的理论分析表明：DFM加矩形窗情形确实有显式校正公式；但对其他窗函数，校正公式要么不存在，要么过度复杂，因而不具有实用性。

1 CSM存在简单校正公式的原因

对周期信号和平稳信号，所使用的窗函数一般均为对称。仔细研究CSM校正公式的推导过程，可以发现：它之所以简单是因为常见对称窗函数w(t)的频谱W(ω)具有如下的两个特性。

特性1常见的对称窗函数的频谱W(ω)一般可以表示为如下形式：

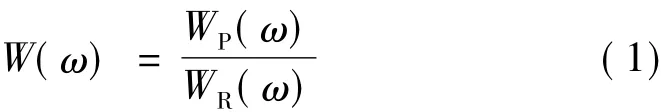
其中：WR(ω)为实有理分式，有的甚至为实多项式；WP(ω)是由三角函数构成的超越实函数。

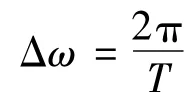
不失一般性，本文仅考虑WP(ω+Δω)=－WP(ω)的情形。

对于单频复解析信号 xa(t)=A0exp(jφ0+jω0t)加w(t)的傅里叶变换为：

记主瓣内相邻的两条FFT谱线ω1和ω2对应的频谱为X1和 X2，即：

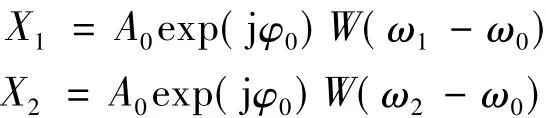
由于FFT的谱线间隔Δω=ω2－ω1=2π/T，因此二者的比值为：

其中利用了特性1和特性2。正因为这两个特性，X1和X2的超越部分抵消而使得X2/X1仅为ω0的有理函数，进而才有可能建立简单的校正公式。

比如将汉宁窗 WR(ω)=(ωT/2)［1－(πT/2)2］代入式(2)，立即可以得到它的校正公式。

对于DFM，不再有类似于式(3)的简单比例关系。但是如果能将两个所对应频谱分离，则各自参数应满足这个比例关系。

2 DFM的频率方程

记DFM的信号为：

其中的 Aa，φa，ωa，Ab，φb，ωb分别为两个频率成分的幅值、相位和频率参数。根据傅里叶变换的线性性质，有：

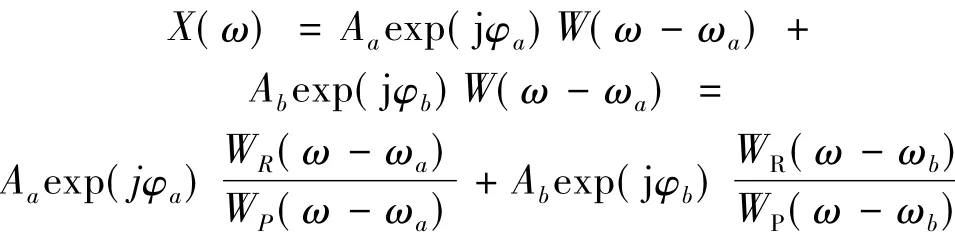
考察双频率主峰附近的四条连续谱线。记频率为ω1～ω4，对应的频谱为 X1～X4，即：

方程组(4)有8个待定参数，但是每个方程都是复方程，虚部和实部各提供一个方程，因此有8个方程。但是本文不直接解这8个方程，而是利用特性2。根据该特性，方程组(4)的每个方程右端两个分子为：

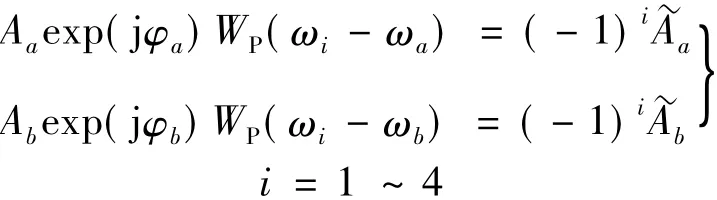
尽管方程组(4)无超越函数，但也未必能够得到显式解。比如高于5次多项式的方程，有所谓的阿贝耳定理，即方程的根不可能用方程系数经过有限次四则运算和开方运算表达出来。退一步，即使有显式解，若其表达式非常复杂，则实用性也不大。如简单的三次多项式方程，它的显式根很复杂。

3 DFM加矩形窗的校正

下面研究DFM加矩形窗简化情形。

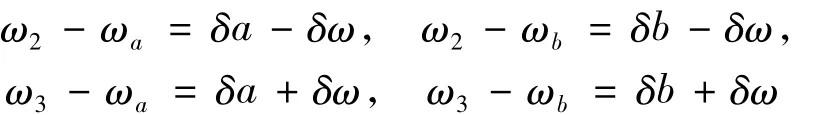
这样方程组(4)的第2和第3两式变为：

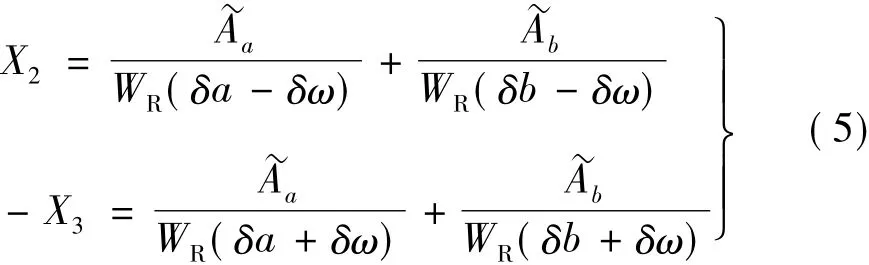
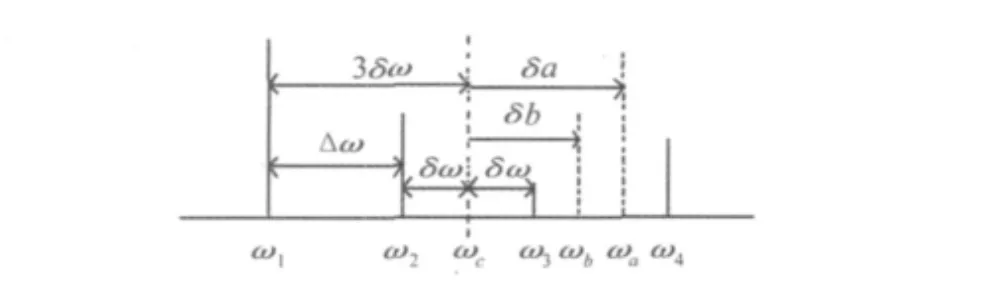
图1 频率参数之间的关系Fig.1 The relationship between the frequency variables

不失一般性，取T=2。将WR(ω)=ω代入式(5)，利用克莱姆法则可以解出：

对于方程组(4)的第1和4式，只需将X1→X2，X3→X4，3δω→δω 代入式(6)即有：

将方程(8)的第1式展开得：

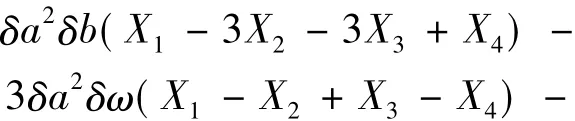
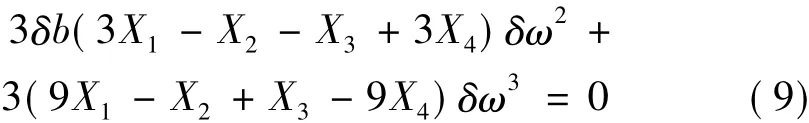
将方程(8)第2式作类似展开，然后与式(9)相减，并消去公因式δa－δb得到：

式中：

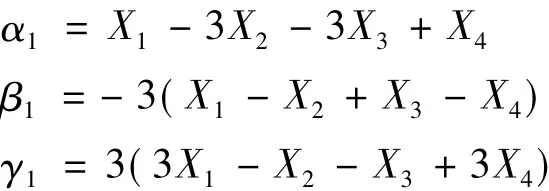
将式(10)的第一项δaδb表示出来：

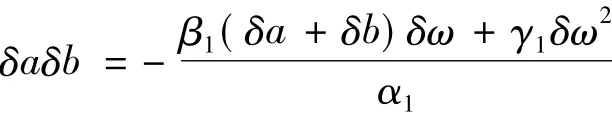
然后代入式(9)的第1项，经整理可得另外一个方程：

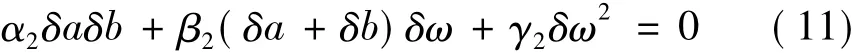
其中：

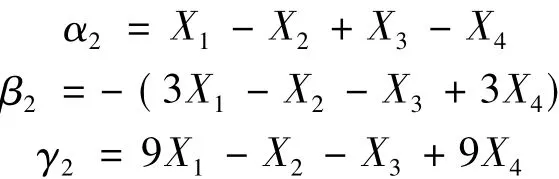
联立式(10)和式(11)，可以解出：

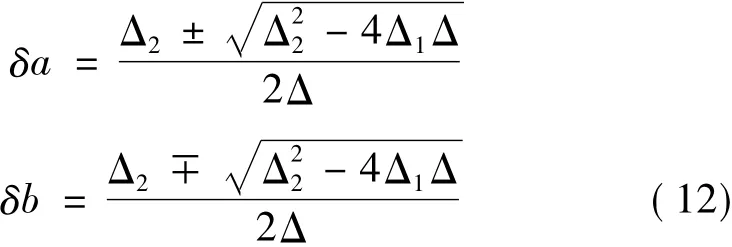
其中Δ，Δ1和Δ2是中间变量，具体为：

由式(12)可以看出频率校正量仍然仅与频谱比值有关。但是对于DFM，离散谱线在复数平面内不再共线［11］，因此虚部和实部都出现在校正公式上。

由于Δ，Δ1和 Δ2均为复数，因此式(12)中－4Δ1Δ是否大于零并不重要。在理论上δa，δb应该全为实数，但是由于误差存在，很难保证其虚部为零，通常取其实部作为δa，δb的近似即可。

由图1的关系，可以得到校正后的频率：

以上是针对时间零点位于窗函数中心建立的公式。对于常用软件包的FFT，零点位于窗口最左侧。根据傅里叶变换的时移性质，FFT的奇数条谱线将附加一个π相位，而偶数条谱线不变。因而所有推导过程和最终结果应将 －X1→X1，－X3→X3。

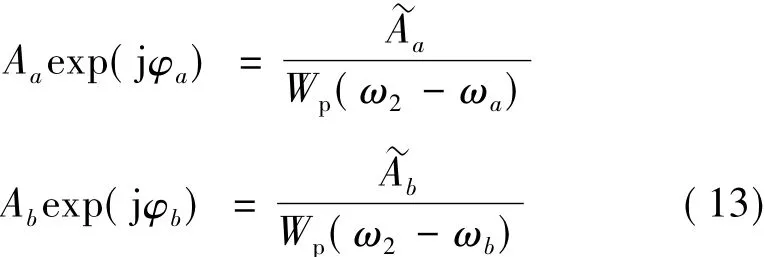
由式(12)的推导过程可以看出，如果将矩形窗换成更复杂函数，则无法得到平行于式(10)和(11)的二次多项式方程，因此校正量虽然与频谱的比值存在确定关系，但是显式表达式将很复杂或者根本就得不到。

4 考核结果与讨论

为了验证式(12)和式(13)的正确性，以及评价它们的实用性，计算参数取T=2，FFT的长度N=1 024。因此，ΔT=T/N=1/512，Δω =2π/T=π。DFM 信号的两个成分为：成分1为强幅成分，参数有两组，即Aa=10，ωa=100.05Δω，φa= π/3 和 Aa=10，ωa=100.55 Δω，φa=π/3，前者接近整周期采样，后者接近半周期采样；成分2为弱幅成分，Ab=1，φb=5π/4。为了细致考核校正公式的效果，ωb在一个范围内取值，即ωb=ωa+ρΔω，其中 ρ=0.3～3Δω。

仿真考核的误差如图 2 所示，其中 εω/Δω，εA，εφ分别为校正后的频率绝对误差、幅值相对误差和相位误差。

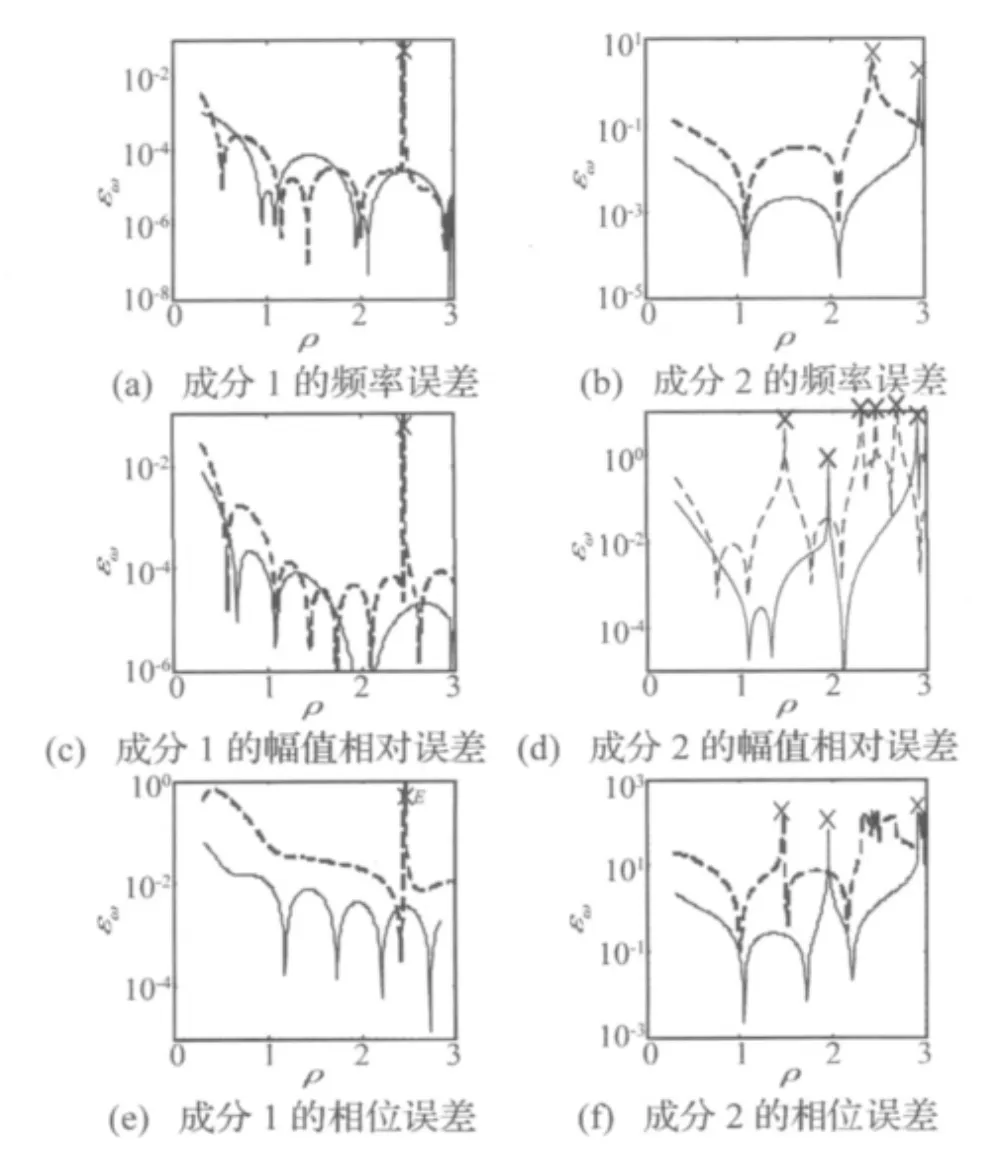
图2 仿真考核的误差特性Fig.2 The error characteristics of the tested example

由图2可以看出，强幅成分的参数精度很高，误差的总趋势随两个频率的分离而下降，当ρ＞0.5之后，εω只有万分之几个 Δω，幅值相对误差量级不超过10－4，相位误差也只有零点几度，且整周期采样与否对幅值和频率的精度影响不大(但成分1是否为整周期采样对成分2的精度影响比较大)。

对影响误差的各种因素比较发现：对误差影响最大的因素是FFT的矩形积分法对精确积分接近程度［12］，特别是窗函数两端权不为零，而数值积分又没有计入这个值的影响。

在成分1的误差曲线上标有X的点，该点附近的误差很大，其原因是式(12)中的Δ→0，因此数值上出现奇异。在校正实施中必须检查这个值，以确定结果的可靠性。如果不考虑这一点，根据误差随频率差而总体下降的趋势，式(12)也适用于CSM的频谱校正。

弱幅成分的参数识别误差较大，但当ρ=0.5～2(即若两成分频率间隔界于 0.5Δω ～2.0Δω)，则频率误差不超过0.1Δω，幅值相对误差低于5%，相位误差在几度范围之内，大体可满足工程精度的要求。

但是随ρ继续增大，弱幅成分的参数误差趋势并非继续降低。这是因为随ρ增大，弱幅成分对强幅成分主峰附近的频谱贡献越小，因而利用强幅成分主峰周围谱线估计的弱幅信号参数的精度越来越差，尤其是奇点(图中标有X的点)频度也加增大。因而对于弱幅成分，如果ρ＞2，不如采用CSM校正公式更为可靠。

弱幅成分的频率估计奇点往往由Δ=0所造成，但式(13)的Wp(ω2－ωa)也会导致幅值和相位的估计奇点。

5 结论

分析了单频率模型的频谱存在简单校正公式的原因。原因是常用窗函数的谱函数可以分解为超越函数与有理分式的乘积，前者对离散谱线间隔有周期性。利用这个特性很容易建立单频率模型的加对称窗的频谱校正公式。将该特性用于双频率模型(DFM)，也可以得到对应的频率方程，但是其关系非常复杂。除了加矩形窗外，其他窗情形涉及到高于2次的多项式方程，因此显示校正公式可能不具有实用性或根本不存在。

对于DFM加矩形窗，频率校正量满足二次多项式方程，因此可以写出其显式解，但是其复杂性远远超出单频率模型的校正公式。采用含幅值差异较大的两个频率成分的信号，对这组显式校正公式进行了考核。结果表明，对于强幅成分，在工程精度内可以认为无误差，而对弱幅成分，当两频率间隔在0.5～2个频率分辨率范围之内，误差在工程精度上可以容忍。如果频率相距比较大，还是各自采用单频率模型为宜。

该方法的噪声特性需要进一步探讨。

［1］沈玉娣，刘 雄，赵振毅.机械故障诊断－FORTRAN源程序汇编［M］.西安：西安交通大学出版社，1990.

［2］黄迪山.FFT相位误差分析及实用校正方法［J］.振动工程学报，1994，7(2)：185－189.

［3］谢 明，丁 康.频谱分析的校正方法［J］.振动工程学报，1994，7(2)：172－179.

［4］丁 康，谢 明.离散频谱三点卷积幅值校正法的误差分析［J］.振动工程学报，1996，9(1)：92－98.

［5］丁 康，钟舜聪，朱小勇.离散频谱相位差校正方法研究［J］.振动与冲击，2001，20(2)：52－55.

［6］朱利民，钟秉林，黄 仁.离散频谱多点卷积幅值修正法的理论分析［J］.振动工程学报，1999，12(1)：120－126.

［7］丁 康，张晓飞.频谱校正理论的发展［J］.振动工程学报，2000，13(1)：14－22.

［8］段虎明，秦树人，李 宁.离散频谱的校正方法综述［J］.振动与冲击，2007，26(11)：138－144.

［9］谢 明，丁 康.两个密集频率成分重叠频谱的校正法［J］.振动工程学报，1999，12(1)：109－114.

［10］陈奎孚，张森文.利用三条谱线计算频率紧邻的两个成分的参数［J］.振动工程学报，2004，17(2)：153－158.

［11］谢 明，丁 康，莫克斌.频谱校正时谱线干涉的影响及判定方法［J］.振动工程学报，1998，11(1)：22－28.

［12］陈奎孚，焦群英，高小榕.改善FFT精度的2种算法比较［J］.中国农业大学学报，1996，1(6)：74－79.