影响声波全波列测井速度分析的因素剖析

沙振海

(铁一院集团甘肃铁道综合勘察院，甘肃兰州730000)

影响声波全波列测井速度分析的因素剖析

沙振海1

(铁一院集团甘肃铁道综合勘察院，甘肃兰州730000)

目前，速度分析是声波全波列测井提取纵、横波速度的必要流程。本文介绍了井场中的声波波形成分，提出了一种相似相关速度分析算法，并在其基础上深入研究了影响速度分析结果的关键因素，如带通滤波，窗口宽度，总叠加时间，以及低速地层等等。通过讨论分析，给出了这些处理参数在速度分析中的取值，它对精确提取岩石纵、横波速度有着重要的指导意义。

速度分析声波全波列测井声波波形相似相关算法

Sha Zhen－hai．Factors with influence on velocity analysis of full wave sonic logging［J］．Geology and Exploration，2012，48(4):0784－0789．

1 引言

声波全波列测井的主要作用是为工程提供岩石的纵、横波的速度。怎样从复杂的声波全波列数据(FWS)中提取出可靠的横波速度一直是测井研究的重要课题。早期主要是根据不同性质的波，通过波形识别法、泊松比法来拾取横波(董清华，2000;曹正良等，2005);当地层横波速度小于井液速度时，全波列数据没有横波，则需通过对斯通利波的分析来计算地层横波速度;随着数字技术的发展，则通过相关对比法、相似相关法来提取横波;近年来阵列声波测井则出现了二维谱处理技术和相位相关法(王冠贵，1988;刘天佑，2004)。

相似相关法算法相对简单、计算效率较高、速度谱效果较好，在测井处理成图软件中应用普遍。除了地层速度、探管声系参数对速度分析结果造成影响外，还有数据预处理、处理参数的不同也会对速度分析结果造成较大的影响(洪有密，1998;张胜业，2004)。本文旨在对这些因素进行分析研究，为提高速度分析效果提供有益的帮助。

当然，要做好速度分析，则需要对井场中的声波波形的物理成因和速度分析算法有深入的理解。

2 井场中的声波波形成分

在钻孔中，处于井液中的声波探管发射的声波脉冲经过井液、井壁岩石等转播到接收器，其接收声波波型的主要成分有滑行纵波、滑行横波、假瑞利波和斯通利波(沈建国，2004;张广智等，2011;沈永进等，2012)。

滑行纵波是一种体波，无频散。若源距选择合适，在全波列中，它是首波，且具有传播速度快，频率高，幅度小的特点。接收器接收的滑行纵波其实是PPP波，即在井液中以P波的形式传播且以第一临界角入射到井壁，在岩层中产生折射波，以滑行纵波(P)的形式传播，再后又折回井液中，以P波的形式传播到接收器。

滑行横波也是一种体波，无频散。若源距选择合适，在全波列中，它是次首波，其传播速度比纵波小，频率比纵波低，幅度比纵波大。接收器接收的滑行横波其实是PSP波。只要滑行横波速度大于井液速度，接收器就能接收到此波，但若小于井液声速，全波列中就没有滑行横波。

假瑞利波是一种界面波，沿井壁界面传播，其传播速度介于地层横波速度与井液声速之间。它是多模式波，每种模式波具有自己的频散曲线，且有自己的截止频率。只有声源频率高于截止频率时才能激发此种模式波。在截止频率处相速度等于地层的横波速度，随着频率的增高，相速度下降较快，最后趋近于井液泥浆速度。

斯通利波也是一种界面波，沿井壁界面传播，其传播速度低于井液速度。它只有一种模式波，且频散轻微，无截止频率(章成广等，1990;T．O．Boulbet［F］et al，1994)。

3 相似相关速度分析算法

对全波列数据(FWS)集的每一个深度点，我们都可以画出如图1所示的时间－道距(Time［μs］－Distance［m］)波列图，其中Tx是发射点，Rx1、Rx2、Rx3…为接收点，其波列在时间轴方向延伸。在图中，我们可以通过发射点(坐标原点)画出一系列不同斜率(Slope)的直线，每一条直线的斜率用时间与距离的比来表示慢度(Slowness，μs/m，速度的倒数) (高尔根，2000;王德利等，2001;孙志峰等，2011)。对给定慢度的直线，可以计算出与Rx1、Rx2、Rx3…波列的时间交点t，并计算交点处声波信号振幅的相干度(Coherence)，其计算公式如下:

其中:i是Rx1、Rx2、Rx3…不同的道;t是给定慢度Slowness的直线与波列的时间交点国;j是窗口宽度。

在一个时间窗口j内，(1)式是所有道叠加后的能量与每一道能量和的比值，描述了这些点振幅的互相关(cross－correlation)程度(Willis．M．E，1983; Kimball．C．V，1984;Lang．S．W，1987;Kimball．C．V，1998;Geerits．T．W et al，2003)。

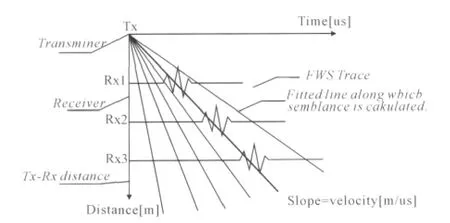
图1 速度分析扫描原理Fig．1 Diagram showing the principle of velocity analysis scanning

这样，我们就可以用FWS的格式存储(1)式计算的结果。所不同的是在每一个深度点，用慢度代替了时间，用相干度St代替了波列的振幅，成为速度谱。

在具体计算时，除了窗口宽度j的大小要考虑外，还有另一个因素就是:由于井液的速度较慢，降低了纵、横波的传播速度，使得穿过这些波的直线并不与原点(发射点Tx)相交，而是有一个偏移量，这会对速度分析的结果造成影响。算法设计了一个总叠加时间(Total Time Stack)，如图2所示，它包含了窗口宽度j，且j在总叠加时间内平行移动，并把每次计算的结果叠加起来作为给定的速度谱。

窗口宽度j应该包含一个波长的波，考虑声波测井的发射频率23 kHz，其可能的最高频率为46 kHz，则对应的波长为21 μs，因此j的范围为15～35 μs较为合适。

总叠加时间(Total Time Stack)主要是低速的井液造成的，与井径有关。一般设置为50 μs，可以依据井径的大小调整，通过试算确定。

图2 总叠加时间和窗口宽度Fig．2 Total time stack and window width

4 速度分析结果的影响因素

本次处理的FWS数据是由英国RG公司的单发三收全波列探管(Slim－Hole Full－Waveform Triple Sonic Probe)测得。其收发距几何参数为0．6 m (Rx1)，0．2 m(Rx2)，0．2 m(Rx3)，发射频率23 kHz，采样间隔为4 μs，采样长度512×16 Bit。

本次处理采用ALT(Advanced Logic Technology)公司开发的WellCAD3．2软件平台的FWS模块。其算法为文中第3节所述的相似相关算法。

以下就不同滤波方法，速度分析中的窗口j、总叠加时间(TotalTimeStack)，以及低速地层对速度分析的影响进行讨论(Advanced Logic Technology，2009;Block．L．V，1991)。

4．1 滤波方法对速度分析的影响

图3是分别在原始数据(左)、移动平均(中)、带通滤波(右)情况下的速度分析结果(j=25，Total-TimeStack=50)。从图中可以看到，在上述三种情况下，横波及其后续波谱(假瑞利波、斯通利波)没有受到滤波方法的影响，慢度谱相似，变化不大;但只在带通滤波情况下，纵波谱清晰可辨，而在原始数据和移动平均情况下，纵波谱与前方干扰连成一片(较宽的黑色)，无法分辨。

分析原因认为通过(1)式计算的相干度，与信号的强度无关，只与信号的相似相关性有关，而FWS数据在纵波(首波)接收之前，记录的数据有一个很小的背景底，它们具有相同的正或者负的关系，信号性质相同，其相干度得到了增强，在速度分析波谱中与纵波谱混在一起，使纵波谱无法分辨。通过移动平均处理的数据，在纵波数据之前，其背景底数据的正或者负的关系没有发生变化，速度分析波谱与原始数据是一样的。但在带通滤波后，纵波之前的数据，其或正或负，并不相似相关，速度分析波谱能量降低，使纵波谱分辨率明显提高。

4．2 窗口宽度对速度分析的影响

图4是TotalTimeStack=50时，窗口宽度j分别为15、25、30、35情况下的速度分析结果。从图中可以看到四种情况下，纵、横波及其假瑞利波、斯通利波的慢度谱依次可辨，但在细节上又有一些差别:①从纵波谱来看，145～147．5 m深度A处，j=15的椭圆形位置不可分辨，与之对应j=25、30、35则出现微弱、较强、微弱的变化;从波谱的连续性、相干强弱来看，j =30的效果较好，易于捡取;另外j=15的波谱前面(如B位置上下)存在一些相干干扰，而在j=30、35则较为干净，且波谱较窄，慢度分辨率较高;②从横波谱来看，j=15的相干度较弱，其他较强;j=35的分辨率较高;③后续的斯通利波谱差别不大;但假瑞利波，j=15时慢度分辨率较差，j=35时相干度较弱，效果较好的是j=25的情况。综上所述，从纵波、横波连续性、分辨率来看，j=30时效果较好。

图5是从图4的结果中拾取的P、S波(左、右)慢度曲线。窗口宽度j=15～35间，纵波慢度整体表现为越来越小(速度则越来越高)，比较变化平稳的153～160 m段，速度差异从3900～5400 m/s，差别较大;而横波慢度，除j=15稍高外，其他的一致性较好。

考虑本段岩性为闪长斑岩，速度5000 m/s左右，则窗口宽度j=30较为合适。

4．3 总叠加时间对速度分析的影响

图6是窗口宽度j=30时，总叠加时间TotalTimeStack分别为30、50、75、90情况下的速度分析结果，其最大相干度分别为17．8、29．7、44．2、52．8，基本上平均最大相干度约为0．59/μs，图中的显示是用最大相干度归一化的结果。从图中可以看到四种情况下，各波谱差别不大，但在细节上TotalTimeStack=90的纵波谱要窄一点，假瑞利波谱相干度要弱一点。

图7是由图6速度分析结果拾取的纵波(左)、横波(右)慢度的比较图。图7(右)显示横波慢度曲线基本一致，与TotalTimeStack关系不大。纵波慢度(左)曲线趋势一直，但随着TotalTimeStack的增加(30～90)，纵波慢度减小约20 μs/m(速度从4760～5260 m/s)，速度差达500 m/s，约10%;其中TotalTimeStack为75、90的纵波慢度差异较小(小于5 μs/m)，速度差100 m/s左右，约为2%。

综上认为TotalTimeStack=75的效果较好(j= 30)。

图7 总叠加时间和P波、S波慢度Fig．7 Total time stack and slowness of P－wave and S－wave

4．4 低速地层的速度分析波谱

图8是一个典型的低速地层的速度分析结果。与前述速度分析结果四条清晰可辨波谱相比，图8显示斯通利波谱(1160 m/s)前面只有一条清晰的速度谱。依据井场波形成分分析，26～42 m间是纵波速度为1800 m/s左右的低速层，42～47 m间是纵波速度为2800 m/s左右的低速层，这两段横波谱都不存在。因此当出现小于2800 m/s纵波低速层时，通过声波全波列测井速度分析一般不可能直接提取横波速度。特别注意，不要误把斯通利波当做横波来拾取。

理论分析认为，当横波的速度低于井内流体的速度时，就接收不到滑行横波。对Vp=2800 m/s的地层，纵、横波速度比一般都大于2，因此Vs一般也小于1400 m/s，低于井内流体的速度，这时需要通过斯通利波法来求解横波速度，具体求法参考文献。

5 结论

通过上述分析，在进行声波全波列测井速度分析时:

(1)在速度分析前，对FWS应进行带通滤波，这样可以消除纵波谱前的相干干扰，提高纵波慢度的分辨率;

(2)依据声波探管的发射频率23 kHz及实际比较，速度分析的窗口宽度应该在25～35 μs为好，对应的最高声波频率为28～40 kHz，与带通滤波的高截止频率相当，本文推荐j=30 μs;

图8 典型低速地层速度分析结果Fig．8 Typical result of velocity analysis to low－velocity strata

(3)总叠加时间TotalTimeStack主要受井径、井内流体速度的影响，一般为50～100 μs，要通过试算取得，原则是各波谱清晰，拾取的纵波谱变化不大;

(4)纵波速度小于2800 m/s的低速地层，速度分析结果一般没有横波谱，横波需要通过斯通利波法求取。

致谢在本文撰写过程中，教授级高工韩永琦给予了倾心指导与帮助，海洋工程师也给予了帮助，在此深表谢意!

Advanced Logic Technology．2009．User's Guide for WellCAD4．3，Book4－FWS Module［M］．ALT:2009．02．27

Block．L．V．1991．Velocity analysis of multi－receiver full－waveform acoustic－logging data in open and cased holes［J］．Log Analyst，188－200

Cao Zheng－liang，Wang Ke－xie，Xie Rong－hua．2005．Three method comparison and application of array acoustic logging data dispersion analysis［J］．Chinese Journal of Geophysics，48(6):1449－1459(in Chinese with English abstract)

Dong Qing－hua．2000．Study of numerical modeling for engineering seismic prospecting［J］．Geology and Prospecting，36(4):56－59(in Chinese with English abstract)

Gao Er－gen，He Chuan－song．2000．2－D Robust iterative velocity inversion of acoustic wave equation［J］．Geology and Prospecting，36 (5):54－58(in Chinese with English abstract)

Geerits．T．W，Tang．X．M．2003．Centroid phase slowness as a tool for dispersion correction of dipole acoustic logging data［J］．Geophysics，68 (1):101－107

Hong You－mi．1998．Well logging principle and integrated interpretation［M］．Dongying，Shandong:Press of the University of Petroleum:44－79(in Chinese with English abstract)

Kimball．C．V．1984．Semblance processing of borehole acoustic array data［J］．Geophysics，49(3):274－281

Kimball．C．V．1998．Shear slowness measurement by dispersive processing of the borehole flexural mode［J］．Geophysics，63(2):337－344

Lang．S．W．1987．Estimating slowness dispersion from arrays of sonic logging waveforms［J］．Geophysics，52(4):530－544

Liu Tian－you．2004．Application of geophysical on data acquisition and processing［M］．Beijing:China University of Geosciences Press:269－274(in Chinese)

Shen Jian－guo．2004．The basis on acoustic application［M］．Tianjin: Tianjin University Press:89－106(in Chinese)

Shen Yong－jin，Shen Jian－guo，Han Qing－bang，Yu Xiang－yu．2012．The character of acoustic logging waveforms in low permeable sand shale stratum［J］．Progress in Geophysics，27(2):809－816 (in Chinese with English abstract)

Sun Zhi－feng，Fan Guan－min，Meng Jie．2011．A adaptive function method of extracting phase slowness of dispersive wave from acoustic logging［J］．Journal of Jilin University(Earth Science Edition)，4 (4):1239－1245(in Chinese with English abstract)

T．O．Boulbet［F］，KUSO．B．Zhen Si．Xu Yun Trans．1994．Porous medium acoustics［M］．Beijing:Petroleum Industry Press:180－193(in Chinese)

Wang De－li，He Jiao－deng，Han Li－guo．2001．High－resolution velocity analysis of phase correlation statistics［J］．Oil Geophysical Prospecting，36(2):198－203(in Chinese with English abstract)

Willis．M．E．1983．Automatic P and S velocity determination from full waveform digital acoustic logs［J］．Geophysics，48(12):1631－1644(in Chinese with English abstract)

Wang Guan－gui．1988．Acoustic logging theory and application［M］．Beijing:Petroleum Industry Press:93－96(in Chinese)

Zhang Cheng－guang，Wang Guan－gui．1990．Study of Pseudo Rayleigh wave and Stone lee wave characteristics and shear wave frist break point［J］．Geophysical Well Logging，6:385－291(in Chinese with English abstract)

Zhang Guang－zhi，Liu Hong，Yin Xing－yao，Wang Dan－yang．2011．Collation method research of acoustic logging data in seismic interpretation．Chinese［J］．Geophys，26(6):2055－2063(in Chinese with English abstract)

Zhang Sheng－ye，Pan Yu－ling．2004．Application of geophysical theory［M］．Beijing:China University of Geosciences Press:409－419(in Chinese)

［附中文参考文献］

曹正良，王克协，谢荣华．2005．三种阵列声波测井数据频散分析方法的应用与比较［J］．地球物理学报，48(6):1449－1459

董清华．2000．工程地震勘探数值模拟研究［J］．地质与勘探，(4):56－59

高尔根，贺传松．2000．二维声波方程稳健迭代速度反演［J］．地质与勘探，(5):54－58

洪有密．1998．测井原理与综合解释［M］．山东东营:石油大学出版社:44－79

刘天佑．2004．应用地球物理学数据采集与处理［M］．武汉:中国地质大学出版社:269－274

沈建国．2004．应用声学基础［M］．天津:天津大学出版社:89－106

沈永进，沈建国，韩庆邦，余翔宇．2012．低渗砂泥岩地层的声波测井波形特征［J］．地球物理学进展，27(2):809－816

孙志峰，樊官民，孟杰．2011．一种提取声波测井频散波相慢度的适应函数方法［J］．吉林大学学报(地球科学版)，4(4):1239－1245．

王德利，何焦登，韩立国．2001．相位相关统计高分辨率速度分析［J］．石油地球物理勘探，36(2):198－203

王冠贵．1988．声波测井理论基础及应用［M］．北京:石油工业出版社:93－96

章成广，王冠贵．1990．伪瑞利波和斯通利波的特性及横波首至的研究［J］．地球物理测井，6:385－291

张广智，刘洪，印兴耀，王丹阳．2011．地震解释中声波测井资料的整理方法研究［J］．地球物理学进展，26(6):2055－2063

张胜业，潘玉玲．2004．应用地球物理学原理［M］．北京:中国地质大学出版社:409－419

Factors with Influence on Velocity Analysis of Full Wave Sonic Logging

SHA Zhen－hai

(Gansu integrated Engineering Investigation of Railway，Lanzhou，Gansu730000)

Velocity analysis is an essential procedure in the processing flow for extracting rock velocity of P－wave and S－wave from full wave sonic logging data．This paper introduces the acoustic waveform component in the well field，suggests a similar correlation velocity analysis algorithm and studies the key factors which influence the results of velocity analysis，such as band－pass filter，window width，total time stack and low velocity layers．Through discussion and analysis，we gave the values of these procesing parameters in the velocity analysis．This may have very important guiding significance for extracting the rock velocity of P－wave and S－wave accurately．

velocity analysis，full wave sonic logging，acoustic waveform，semblance correlation algorithm

book=7,ebook=176

P631

A

0495－5331(2012)04－0784－6

2012－3－20;

2012－04－26;［责任编辑］郝情情。

沙振海(1968年－)，男，高级工程师，1991年毕业于河北地质学院物探系，获学士学位，主要从事工程物探数据处理与综合解释工作。E－mail:szh626@163．com。