一种新的边缘检测算法研究

肖 梅，张 雷，寇雯玉，苗永禄，刘 伟

(长安大学汽车学院汽车运输安全保障技术交通行业重点实验室，陕西西安710064)

0 引言

模糊神经网络系统综合了神经网络从样本中学习的能力和模糊逻辑系统对不确定性和不准确性的建模能力，适用于处理在提取图像有用信息过程中遇到不确定的情况，故基于神经网络和模糊逻辑系统已经引起了很多研究者的关注［1－6］.研究人员提出新的神经模糊算法(Edge Detection in Noisy Images by Neuro－Fuzzy Processing，EDNINFP)对被噪声污染的图像进行边缘检测［1］.文献［6］定义了一个目标函数，目标函数的值与模板中心点像素的边缘梯度和方向相关，由目标函数值来判断和确定该像素点是否为边缘点.WU［7］提出了一种快速多级模糊边缘检测算法(Fast Multilevel Fuzzy Edge Detection，FMFED).文献［8］提出了一种基于直观模糊集理论(Attanassov’s Intuitionistic Fuzzy Set Theory，AIFST)的边缘检测算法，该算法使用了16个模板，定义一个新的距离测量公式来衡量中心点与相邻点的差异性，作为判断中心点是否为边缘点的标准.笔者提出的边缘检测算法由一个自适应模糊神经网络系统和一个后处理程序组成.

1 算法

本算法中自适应神经模糊推理系统具有4个输入和1个输出，选取了与边缘方向梯度双重信息相关的 4 个目标函数：f1，f2，f3，f4作为自适应神经模糊推理系统的输入.对于自适应神经模糊推理系统的输出值，运用一个后处理程序，采用一个固定的阈值来判断该中心点是否为边缘点.算法结构示意图如图1所示.

图1 算法示意图Fig.1 Algorithm diagram

1.1 自适应神经模糊推理系统的输入

按照边缘的4个方向定义了4个目标函数：f1，f2，f3，f4，分别为垂直方向、水平方向、斜 135°角方向和斜45°角方向(如图2所示)，并且将这4个目标函数作为基于自适应神经模糊推理系统的输入.

首先引入一个3×3模板.模板包含其中心点(像素灰度值标记为p5，其坐标为(x，y))和它的8 个相邻点(像素灰度值分别标记为 p1，p2，p3，p4，p6，p7，p8和 p9).

接着，定义4个边缘方向模板，如图2所示.图中黑色箭头表示模板中心点的边缘方向.根据3×3模板中心点p5的4个可能的边缘方向，定义4个边缘方向模板.垂直边缘方向模板如图2(a)所示，水平边缘方向模板如图2(b)所示，斜135°边缘方向模板如图2(c)所示，斜45°边缘方向模板如图2(d)所示.

然后分别对每一个方向模板内的9个像素划分为2个集合s0和s1，如图2所示，浅灰色标记的像素区域为集合s0，白颜色标记的像素区域为集合s1.

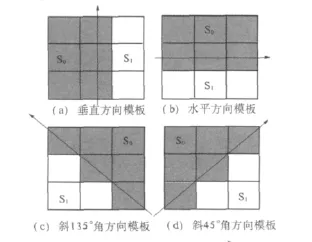
图2 4种边缘方向模板Fig.2 Four directions mask of edge

最后，定义自适应神经模糊推理系统的4个输入 f1、f2、f3、f4并确定目标函数.在 4 个边缘方向模板中，定义Nf为集合s0和集合s1之间基于灰度值的集合之间距离(也可以简称为“集合之间距离”)，Nf越大，2个集合之间的对比度也就越大，模板中心点为边缘点的可能性就越大.集合之间距离Nf定义如公式(1)：

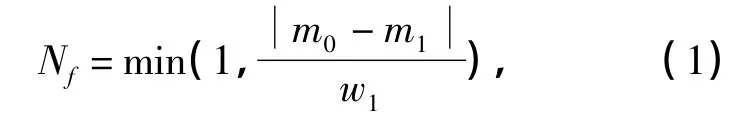
其中，

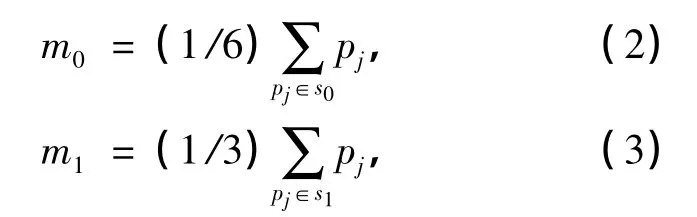
式中：w1为常数，在大量实验基础上，选取数值为90;pj表示3×3模板中第j个像素点的灰度值，j=1，2，…，9.

定义Df为集合s0和集合s1内部像素基于灰度的集合内部距离.Df越小，那么两个集合的致密性也就越高，对于模板中心点而言，被判定为边缘点的可能性也就越大.集合内部距离函数Df定义如公式(4)：

其中，

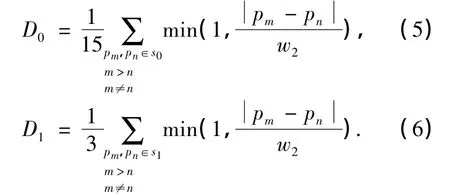
公式(4)中的第一项添加一小项1是为了防止公式(7)中的分母项Df为零;w2为常数，根据大量的实验数据取值为40.

定义一个目标函数fi来表述Nf和Df之间的逻辑关系.i=1，2，3，4 分别代表垂直方向、水平方向、斜135°方向和斜45°方向.目标函数定义见公式(7)

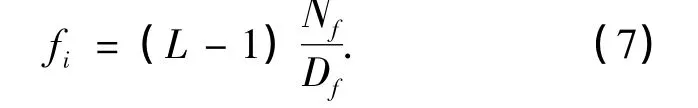
式中：fi表示第i个边缘方向模板的目标函数，fi标准化在［0，L－1］之间;对于256级灰度级的图像L取值为256.fi的值越大，模版中心点为边缘点的可能性也就越大.

1.2 自适应神经模糊推理系统的训练

自适应神经模糊推理系统内部的参数是通过训练、逐步调整得到的.自适应神经模糊推理系统的训练采用混合算法，其中条件参数采用反向传播算法，而结论参数采用线性最小二乘估计算法来调整参数.

训练的输入图像和输出目标图像可以很容易通过计算机进行合成，如图3所示.

图3 训练图像Fig.3 Training image

1.3 基于自适应神经模糊推理系统边缘检测算法的输出

基于自适应神经模糊推理系统边缘检测算法的输出还必须经过一个后处理程序，即将自适应神经模糊推理系统的输出值F和一个阈值T相比较，小于门限值的像素点认为是非边缘点并令其像素值为0，反之认为是边缘点并令其像素值为255.

式中：fe(x，y)就是后处理程序的输出，即边缘检测算法的输出;T为阈值，通常取图像灰度值变动范围值的一半.

2 仿真实验

为了验证笔者提出的边缘检测算法的有效性，采用Algarve大学图像实验室提供的合成图像来 进 行 仿 真 实 验 (http：//w3.ualg.pt/ ～dubuf/pubdat/ledge/ledge.html).

256×256大小的测试图像如图4(a)所示，真实的图像边缘如图4(b)所示.笔者的方法、NF方法、FMF方法和IFS方法的边缘检测结果分别如图4(c)、图4(d)、图4(e)和图4(f)所示.定量评价指标如表1所示.从定量指标看，笔者方法的边缘定位和检出率最好，其它依次是NF方法、FMF方法和IFS方法.这些结论可以从图4中得到直观的印证.

图4 Ledge边缘检测图Fig.4 Edge detection image of Ledge

定量指标采用定位指标Pl和误检率指标

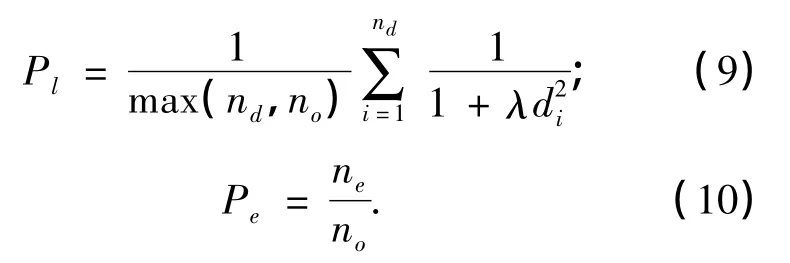
式中：nd是检测出来的边缘点数目;no为原始图像中的边缘点数目;λ为标准常数取值为2，di为检测出的失真的边缘图像中第i个边缘点和与它相关的原始图像中的边缘点之间的欧几里得距离;ne为错误检测出的边缘点的数目.算法的检测结果越准确，得到定位指标Pl的值就越大，误检率Pe的值越小.表1为定位指标和误检率数据.

表1 原始测试图像的定位指标和误检率指标对比Tab.1 The measurements of localization criterion and detection criterion on the original test image

3 结论

笔者提出新的边缘检测算法，使用自适应神经模糊推理系统来解决在图像边缘检测中可能遇到不确定、随机的和多变的情况，得到很好的边缘检测结果.算法的主要优势如下：一是构建了一个只有4个输入一个输出的简洁的神经模糊推理结构，合理的选取了4个输入变量，提高系统运行效率和算法检测的准确性;二是系统的训练利用简单的人工合成图像来进行，解决了神经网络学习资源选取的困难.

［1］YUKSEL E M.Edge detection in noisy images by neuro-fuzzy processing［J］.International Journal of Electronics and Communications，2007，61(2)：82－89.

［2］BECERIKLI Y，KARAN T M.A new fuzzy approach to edge detection［J］.Computational Intelligence and Bioinspired Systems，2005，35(12)：943－951.

［3］ZHUGE Y，UDUPA J K，SAHA P K.Vectorial scalebased fuzzy-connected image segmentation［J］.Computer Vision Image Understanding，2006，101(3)：177－93.

［4］YUKSEL M E.A hybrid neuro-fuzzy filter for edge preserving restoration of images corrupted by impulse noise［J］.IEEE Trans.Image Processing，2006，15(4)：928－36.

［5］ZHOU De-long，PAN Quan，ZHANG Hong-cai.An improved algorithm of edge detection based on fuzzy sets［J］.Journal of Image and Graph，2001，6(4)：353－358.

［6］KANG Chung-Chia，WANG Wen-Jun.A novel edge detection method based on the maximizing objective function［J］.Pattern Recognition，2007，40(2)：609－618.

［7］WU Jin-bo，YIN Zhou-ping，XIONG You-lun.The Fast Multilevel Fuzzy Edge Detection of Blurry Images［J］.IEEE Signal Processing Letters：2007，14(5)：34－42.

［8］CHAIRA T，RAY A K.A new measure using intuitionistic fuzzy set theory and its application to edge detection［J］.Applied Soft Computing，2008，8(2)：919 －927.

［9］AYDIN T，YEMEZ Y，ANARIM E，et al.Multidirectional and multiscale edge detection via M-band wavelet transform［J］.IEEE Trans.Image Process，1996，5(9)：1370－1377.