改进的局部波数法及其在磁场数据解释中的应用

李丽丽，杜晓娟，马国庆

吉林大学地球探测科学与技术学院，长春 130021

改进的局部波数法及其在磁场数据解释中的应用

李丽丽，杜晓娟，马国庆

吉林大学地球探测科学与技术学院，长春 130021

局部波数法是一种进行磁场数据解释的常用方法。现有的局部波数法在进行反演时往往需要计算局部波数的导数，会明显地增大噪声的干扰，为解释结果带来误差。提出3种利用磁异常在不同位置或不同高度上局部波数的简单组合来进行场源体深度及构造指数的计算方法，不需要计算局部波数的导数，降低了噪声的干扰，增强了反演结果的稳定性。通过理论模型试验，证明改过的局部波数法在有无噪声的情况下均能很好地完成异常的反演，其反演结果与理论值之间的差距小于理论值的5%。将其应用于四川某地区磁异常的反演中，其结果与解析信号的欧拉反褶积法的反演结果吻合。

磁场；深度；构造指数；导数；局部波数

0 前言

磁数据解释的主要任务是确定场源体的深度及类型（构造指数）。为此人们提出了很多方法来完成这一任务，有维纳反褶积法［1］、解析信号法［2］、欧拉反褶积法［3－4］、最小二乘法［5－6］、场源参数成像［7］及人工神经网络法［8］等，其中场源参数法是近期应用最为广泛的一种方法。该方法利用局部波数快速地进行场源体反演；但需人为给定研究区场源体的构造指数，而一个地区场源体的构造指数往往是未知的。为了解决这一问题，人们对该方法进行了改进［9－11］，使其能够同时完成深度及构造指数的反演。然而，改进后的方法需要计算局部波数的一阶甚至更高阶导数，对数据精度要求较高，且会增大噪声干扰；当测量点距较大时，高阶导数的计算非常不稳定。Pilkington等［12］在2006年证明局部波数为解析信号［13］的导数，因此局部波数在二维情况下具有不受磁化方向干扰的优点。Salem等［14－15］利用原始局部波数和相位转换后的局部波数完成了异常体位置的反演，并于2008年试验了该方法在三维情况下的应用效果。Keating［16］利用局部波数及其垂直导数对异常体的深度及构造指数进行反演，但是该方法会增大噪声的干扰。

笔者对局部波数法进行改进，采用不同位置和不同高度磁异常的局部波数直接计算场源体的深度和构造指数，不需要计算局部波数的导数，且降低了噪声干扰。

1 改进的局部波数法

对于磁场T而言，其局部波数kx被定义为局部相位θ的水平方向的导数［17］：

局部相位θ被定义为

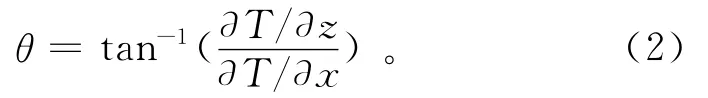
其中，əT／əx和əT／əz分别表示异常T的水平与垂直导数。对式（1）进行微分后得到

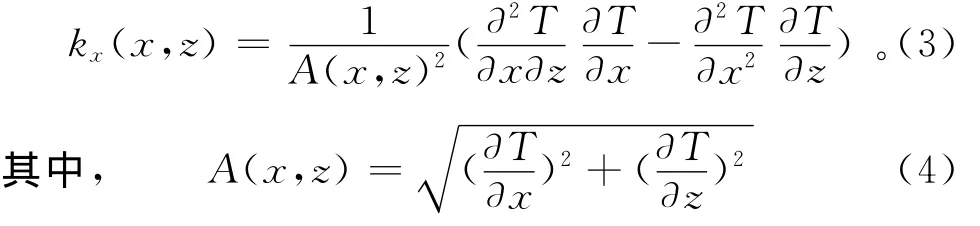
为异常T的解析信号。Smith等［11］推导出水平位置为x0、埋深为z0的磁性体在点（x，z）处引起的局部波数kx的表达式为

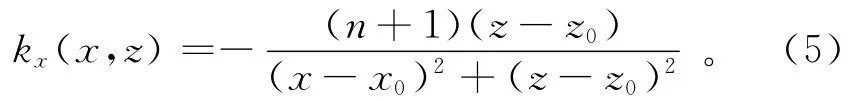
其中，n为与场源体类型对应的构造指数。Stavrev等［18］推导了磁源体类型与构造指数之间的对应关系，其中接触带的构造指数为0，岩墙为1，水平圆柱体为2，点源为3。

异常体的水平位置x0可以通过解析信号和局部波数的极大值来确定。局部波数kx在水平位置x＝x0、垂直位置z＝0处的值为

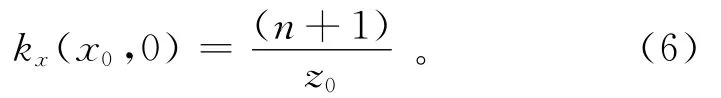
局部波数kx在水平位置x＝x0＋c，垂直位置z＝0处的值为

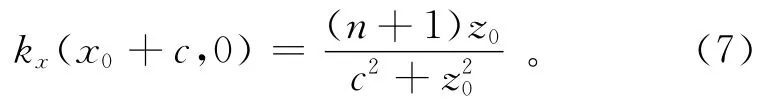
将式（6）与式（7）相除后可以得到

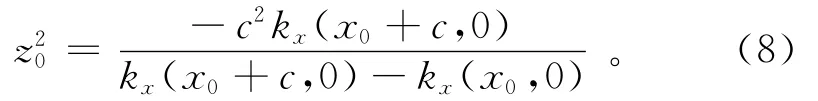
利用方程（8）可获得场源体的深度，然后利用方程（6）计算场源体的构造指数：

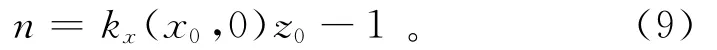
经过以上的推导可以看出，利用局部波数上2个不同水平位置的点依据方程（8）和（9）就可以获得异常体的深度和构造指数。在反演过程中，计算点应选取在场源体中心位置附近；因为在该范围内异常的信噪比较大，得到的反演结果更准确。笔者给出了一种利用不同高度的局部波数kx进行磁异常反演的方法，为了使输出结果更加稳定，采用上延的方法来获得不同高度上的局部波数。局部波数kx在水平位置x＝x0、垂直位置z＝－d处的值为

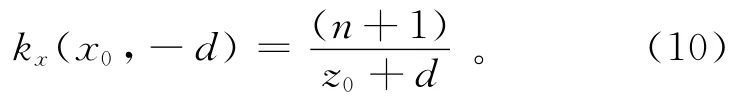
将（6）式与（10）式相除后得到

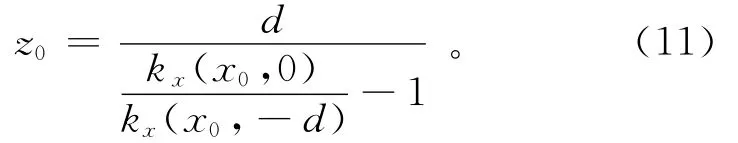
分别计算方程（6）与（10）的倒数然后相减得到

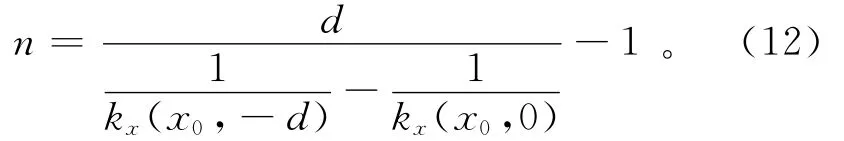
从上述公式中可以看出，利用2个不同高度的局部波数kx，由（11）和（12）式可以得到异常体的深度和构造指数。除上述2种方法外，笔者还提出了另外一种利用相位转换后的局部波数进行磁异常解释的方法。

Salem等［13］定义相位转换后的局部波数kz的表达式：

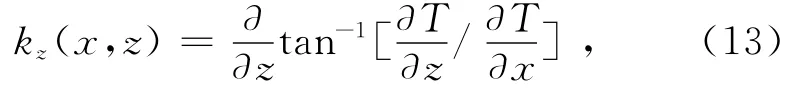
并推导出水平位置在x0、埋深为z0磁性体的局部波数kz在点（x，z）处的表达式为

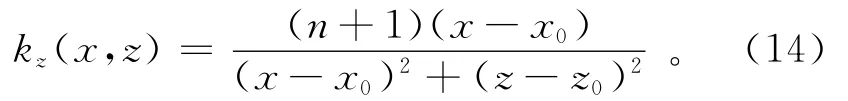
局部波数kz在水平位置x＝x0＋b、垂直位置z＝0处的表达式为

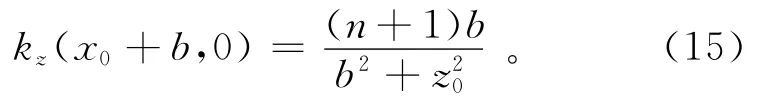
局部波数kz在水平位置x＝x0＋c、垂直位置z＝0处的表达式为

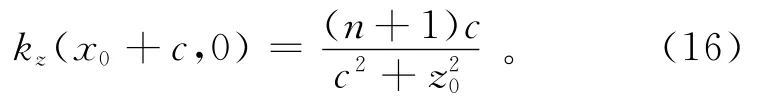
将方程（15）与（16）相除后得到

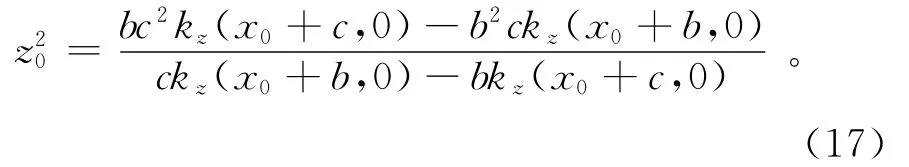
利用（17）式可以得到场源体的深度，然后根据方程（15）计算异常体的构造指数：

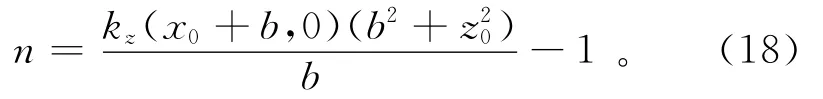
利用方程（17）和（18）就可以计算出场源体的深度和构造指数，考虑反演结果的稳定性，b一般选取为1。

经过以上的推导，笔者给出进行磁性体深度和构造指数计算的3种方法，这3种方法不需要局部波数的导数参与计算，有效地提高了结果的稳定性。在利用上述方法进行反演时，为了提高结果的准确性，计算点应选取在局部波数kz两个极值点之间；因为两个极值点对应于异常体的边界，当测点在异常体上方时其反演结果是最准确的［4］。

2 模型试验

为了试验方法的适用性，设计了如下模型：在长为100km的剖面中点位置处存在一个顶面埋深为4km的岩脉，顶面宽度为10km，磁化强度为20A／km，地磁倾角为60°，磁偏角为0°，测量点距为1 km。利用笔者提出的3种方法对磁异常进行反演，其反演结果为2个计算点之间的水平距离（c）和上延高度（d）的函数（图1），并给出了反演结果与理论值之间的标准偏差（sd）。

从反演结果中可以看出：当水平距离小于14 km、上延高度小于7km时，本文3种方法反演得到的构造指数均与理论值之间的偏差小于0.01，反演得到的深度与真实深度之差小于0.1km，其误差小于理论值的2%，所以本文方法能很好地完成异常的反演，但随着水平距离与上延高度的增大，标准偏差增大，反演结果的精度降低。

在进行实际数据处理时，噪声是必须考虑的一个因素。为了试验方法存在噪声时的应用效果，在图1a的原始异常中加入均值为0、均方差为1nT的随机噪声，采用笔者提出的3种方法对异常进行反演（图2）。

从图2中可以看出，在存在噪声时本文方法的反演结果有一定的波动。笔者采用如下准则来获得最终结果：1）选取水平距离为0～10km的所有深度解，计算其平均值；2）将与平均值差异大于平均值25%（根据实际情况设定）的解去除，重新计算平均值；3）以新平均值为最后深度，计算构造指数。依据该准则获得的反演结果如表1所示。

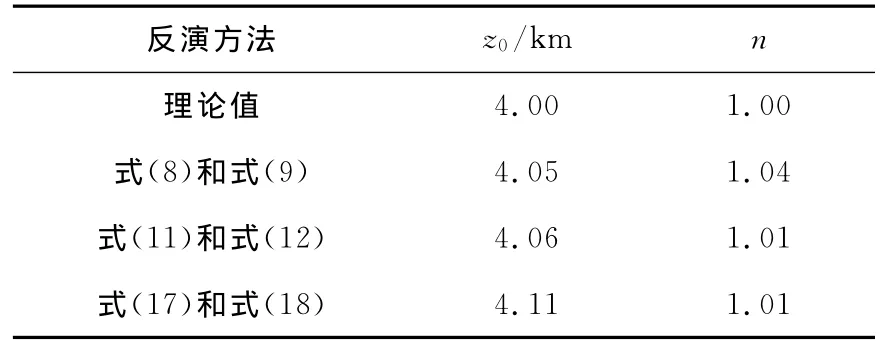
表1 不同方法的反演结果Table 1 Inversion results of different methods

从表1中可以看出，在存在噪声的情况下本文方法的反演结果与理论值之间差距也较小。

为了获得更加准确的结果，可采用向上延拓技术先对异常进行处理，然后再进行反演。笔者对异常进行向上延拓处理，当延拓高度为2km时局部波数已足够圆滑，即局部波数kx为单峰值（图3）。

从反演结果（图3）可以看出，与图2相比，向上延拓后异常反演结果的不规则波动消失，计算反演结果的平均值，式（8）和（9）反演得到的深度为4.01 km，构造指数为1.01；式（11）和式（12）反演得到的深度为4.02km，构造指数为1.01；式（17）和式（18）反演得到的深度为4.01km，构造指数为1.01，因此对异常进行向上延拓处理后反演结果的精度得到提高，其值更加准确。因此，实际数据处理前对数据进行向上延拓处理后会提高反演的精度。

3 实际数据处理

利用笔者提出的方法解释四川某段实测航磁异常（图4）。数据采样间距为100m。将异常向上延拓200m，根据解析信号和局部波数的最大值得出异常体的水平位置在距起始点2 950m处。

从反演结果可以看出：利用不同方法反演得到的构造指数均接近1，表明地质体为一岩墙，反演得到深度的平均值为543m。

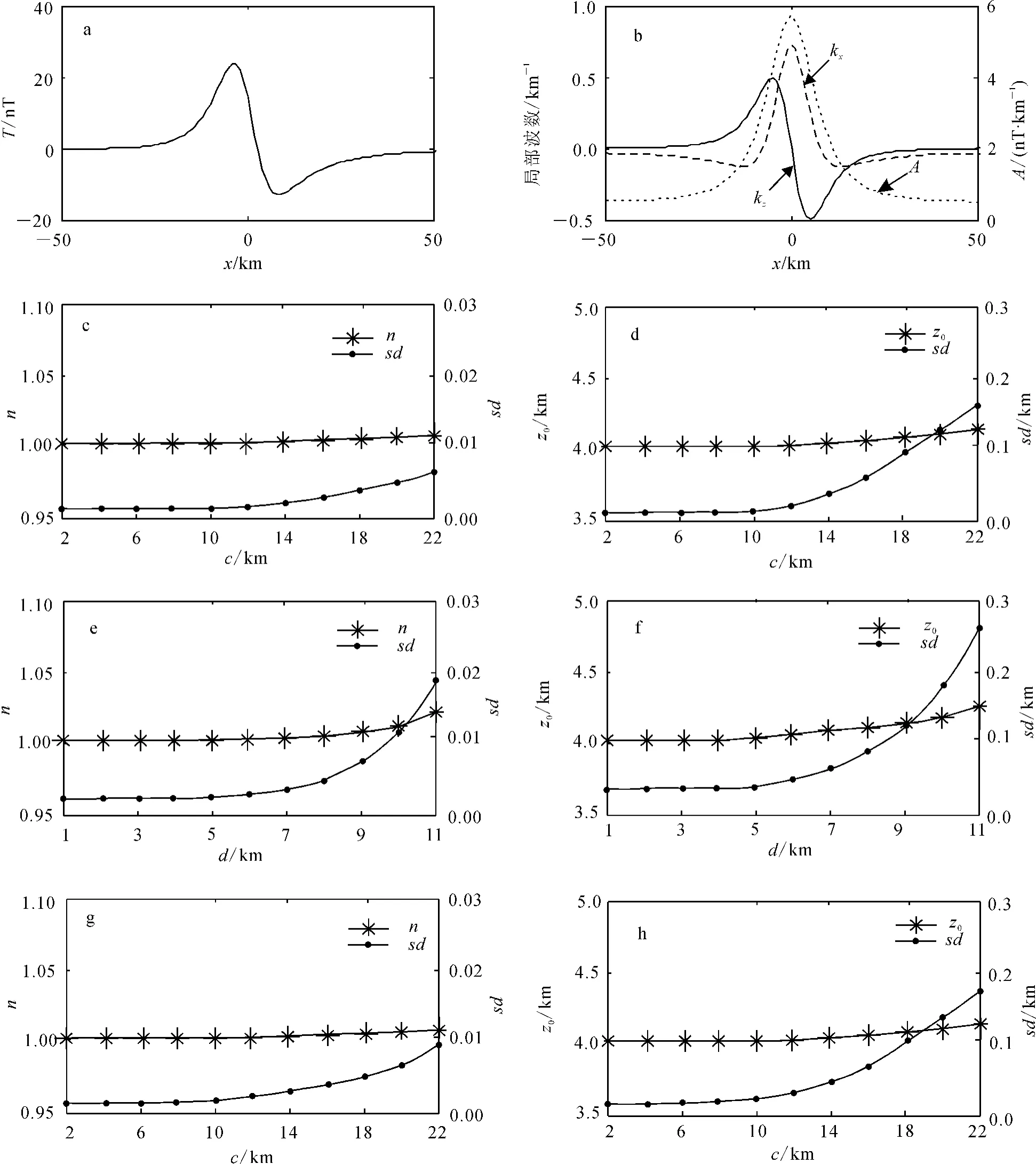
图1 模型理论异常及不同方法的反演结果Fig.1 Theoretical anomaly and inversion results of different methods

该地区没有其他的数据来验证反演结果的正确性，将笔者的反演结果与解析信号欧拉反褶积法［19］的反演结果进行对比。解析信号欧拉反褶积法的反演结果显示异常体的位置在（2 945±7）m，深度为（554.6±18.2）m，构造指数大小为0.98±0.03。这与本文方法的反演结果相一致，表明本文方法反演结果是准确的。

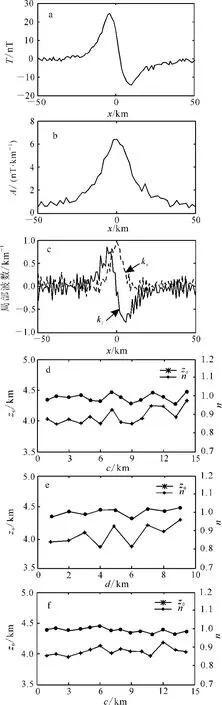
图2 加噪后异常及不同方法的反演结果Fig.2 Noise－corrupted anomaly and the inversion results of different methods

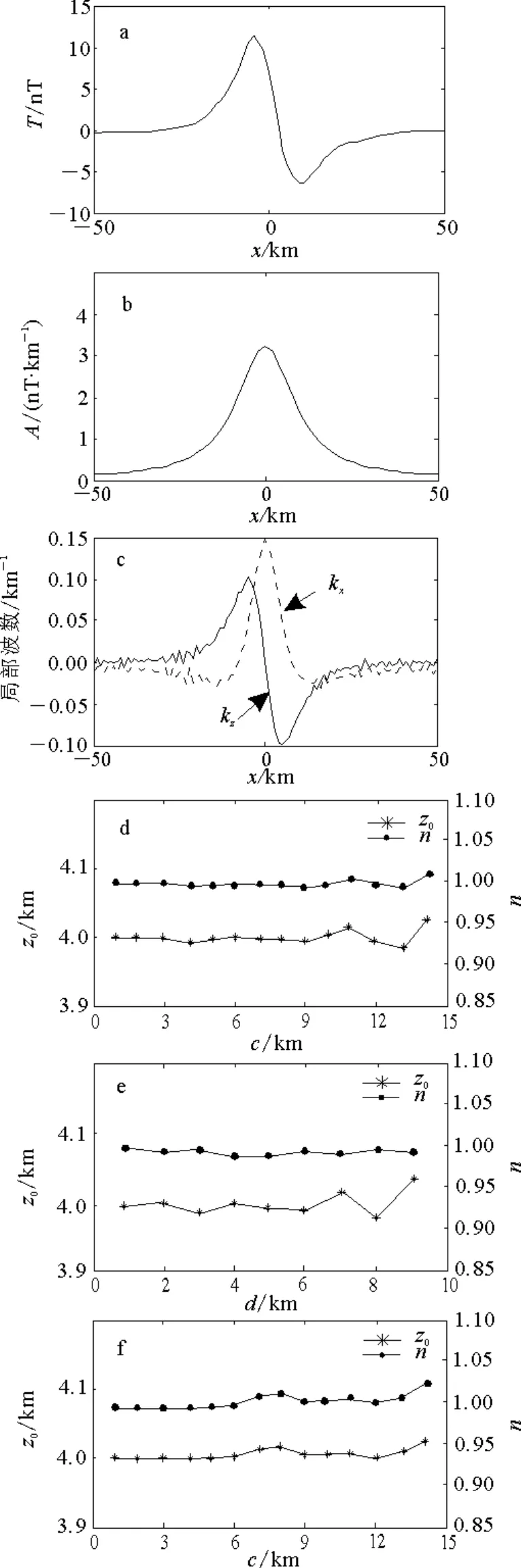
图3 滤波后异常及不同方法的反演结果Fig.3 Smoothed anomaly and the inversion results of the methods

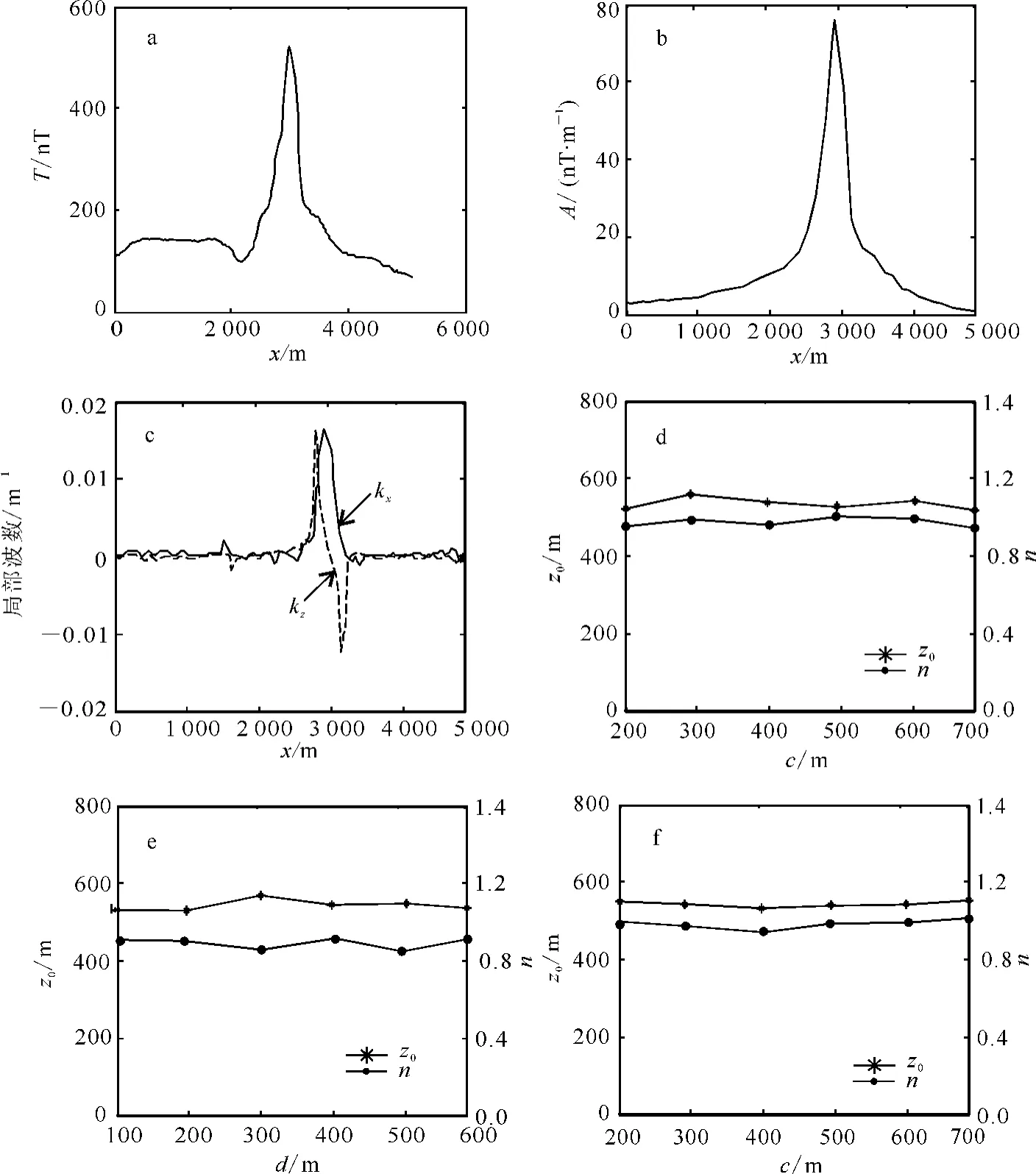
图4 实际航磁异常的反演结果Fig.4 Inversion results of real aeromagnetic anomaly

4 结论

1）笔者提出3种改进的局部波数法进行磁性体反演方法，这些方法仅利用不同水平位置和不同高度的局部波数来进行深度和构造指数的计算，不需要计算局部波数的导数，降低了对数据精度的要求。

2）通过理论模型试验证明，新方法在有无噪声情况下，均能准确地计算出地质体的深度和构造指数。

3）在有噪声情况下，采用向上延拓技术处理数据后可获得更加精确的结果，为实际数据解释提供了理论依据。

4）将新方法应用于四川实测剖面磁数据的解释中，其反演结果与解析信号的欧拉反褶积法的结果相吻合，表明本文方法在实际中也有较好的应用效果。

（References）：

［1］ Hartman R R，Teskey D J，Friedberg J L.A System for Rapid Digital Aeromagnetic Interpretation［J］.Geophysics，1971，36：891－918.

［2］ Nabighian M N.The Analytic Signal of Two Dimensional Magnetic Bodies with Polygonal Cross Section：Its Properties and Use for Automated Anomaly Interpretation［J］.Geophysics，1972，37：507－517.

［3］ Thompson D T.“EULDPH”：A New Technique for Making Computer－Assisted Depth Estimates fromMagnetic Data［J］.Geophysics，1982，47：31－37.

［4］ Reid A B，Allsop J M，Granser H，et al.Magnetic Interpretation in Three Dimensions Using Euler Deconvolution［J］.Geophysics，1990，55：80－91.

［5］ Abdelrahman E M.Discussion on“A Least－Squares Approach to Depth Determination from Gravity Data”by O P Gupta［J］.Geophysics，1990，55：376－378.

［6］ Salem A，Ravat D，Mushayandebvu M F，et al.Linearized Least－Squares Method for Interpretation of Potential Field Data from Sources of Simple Geometry［J］.Geophysics，2004，69：783－788.

［7］ Thurston J B，Smith R S.Automatic Conversion of Magnetic Data to Depth，Dip，and Susceptibility Contrast Using the SPI Method［J］.Geophysics，1997，62：807－813.

［8］ Elawadi E，Salem A，Ushijima K.Detection of Cavities from Gravity Data Using A Neural Network［J］.Exploration Geophysics，2001，32：75－79.

［9］ Thurston J B，Smith R S，Guillon J.A Multi－Model Method for Depth Estimation from Magnetic Data［J］.Geophysics，2002，67：555－561.

［10］ Salem A，Smith R S.Depth and Structural Index from the Normalized Local Wavenumber of 2DMagnetic Anomalies［J］.Geophysical Prospecting，2005，51：83－89.

［11］ Smith R S，Thurston J B，Dai T，et al.ISPI：The Improved Source Parameter Imaging Method［J］.Geophysical Prospecting，1998，46：141－151.

［12］ Pilkington M，Keating P.The Relationship Between Local Wavenumber and Analytic Signal in Magnetic Interpretation［J］.Geophysics，2006，71（1）：L1－L3.

［13］ 马国庆，杜晓娟，李丽丽.利用水平与垂直导数的相关系数进行位场数据的边界识别［J］.吉林大学学报：地球科学版，2011，41（增刊）：345－348.

Ma Guo－qing，Du Xiao－juan，Li Li－li.Edge Detection of Potential Field Using Correlation Coefficient of Horizontal and Vertical Derivatives［J］.Journal of Jilin University：Earth Science Edition，2011，41（Sup.）：345－348.

［14］ Salem A，Ravat D，Smith R，et al.Interpretation of Magnetic Data Using an Enhanced Local Wavenumber（ELW）Method［J］.Geophysics，2005，70（2）：L7－L12.

［15］ Salem A，Williams S，Fairhead D.Interpretation of Magnetic Data Using Tilt－Angle Derivatives［J］.Geophysics，2008，73：L1－L10.

［16］ Keating P.Improved Use of the Local Wavenumber in Potential－Field Interpretation［J］.Geophysics，2009，74（6）：L75－L85.

［17］ Bracewell R N.The Fourier Transform and Its Application［M］.New York：McGraw Hill Book Co，1965.

［18］ Stavrev P，Reid A.Degrees of Homogeneity of Potential Fields and Structural Indicates of Euler Deconvolution［J］.Geophysics，2007，72（1）：L1－L12.

［19］ Keating P，Pilkington M.Euler Deconvolution of the Analytic Signal and Its Application to Magnetic Interpretation［J］.Geophysical Prospecting，2004，52：165－182.

Improved Local Wavenumber Methods in the Interpretation of Magnetic Fields

Li Li－li，Du Xiao－juan，Ma Guo－qing

College of GeoExploration Science and Technology，Jilin University，Changchun 130026，China

Local wavenumber method is a widely used method in the interpretation of magnetic fields，the previous local wavenumber methods need to compute the derivatives of local wavenumber in the inversion，which increase the effect of noise obviously，and bring the errors to inversion results.The authors proposed using the simple combinations of different locations and heights of local wavenumber of magnetic anomaly to compute the depth and structural index of the causative source，and these methods do not need to compute the derivatives of the local wavenumber，which reduce the effect of the noise，and increase the stability of the inversion results.The new methods are demonstrated on theoretical magnetic field data without and with random noise，and the difference between the inversion results and theoretical values is less than 5%of the theoretical values.The practical application of the new methods is tested on real magnetic anomaly from Sichuan basin，Southwest China，the inversion results are consistent with the results computed by the Euler deconvolution of analytic signal.The proposed local wavenumber methods can finish the inversion of magnetic data effectively.

magnetic fields；depth；structural index；derivatives；local wavenumber

book=2012,ebook=558

P631.2

A

1671－5888（2012） 04－1179－07

2011－10－23

国家深部探测技术与实验研究专项项目（SinoProbe－09－01）

李丽丽（1983－），女，博士研究生，主要从事地球物理数据处理与解释方面的研究，E－mail：lilili10＠mails.jlu.edu.cn。