前向平滑MUSIC算法及其FPGA设计*

邓琦新，周 围，2，杜晓雷，闫 杰

（1.重庆邮电大学移动通信重点实验室，重庆400065;2.重庆邮电大学光电工程学院，重庆 40065）

波达方向（Direction of Arrival，DOA）估计在现代通信的许多场合都有广泛的应用，如移动通信中的空分多址、电子侦察和对抗［1］等。现阶段应用在智能天线系统中的DOA估计算法有很多种，典型的有 MUSIC、ESPRIT［2］算法等，其中由Schmidt于1979年提出的MUSIC算法［3］因具有较高的分辨能力而受到人们的青睐。但经典MUSIC算法在估计相干信号的DOA时，算法容易失效。本文研究的改进型MUSIC算法［4］，通过引入空间平滑技术对信号进行预处理，能够对相干信号的波达方向作出精确估计。从而避免了经典MUSIC算法在估计相干信号的DOA时算法失效的问题。

DOA估计在许多应用场合中，都面临着高速实现、小型化、低成本的要求。本文研究的MUSIC算法的FPGA设计，利用FPGA并行处理的优点，实现算法需要的各个处理单元，并通过状态机（State Machine）对算法进行控制，从而满足算法实时性的要求，对于促进DOA估计算法的高速实现有很重要的意义。

1 前向平滑MUSIC算法

空间平滑思想［5］如图1所示。假设有L个信源入射到由M个阵元构成的均匀直线阵，前向平滑MUSIC算法的步骤如下:

步骤1:将线性等距的M个阵元分为q个重叠的子阵列，各子阵列所含阵元个数为p，且满足p+q-1=M。

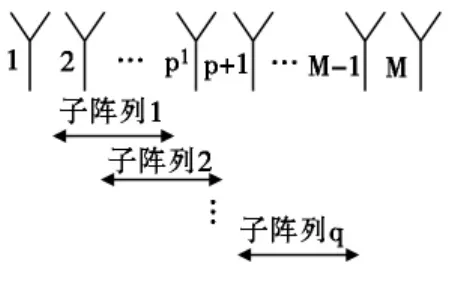
图1 前向空间平滑

步骤2:第l个子阵列的接收矢量为:

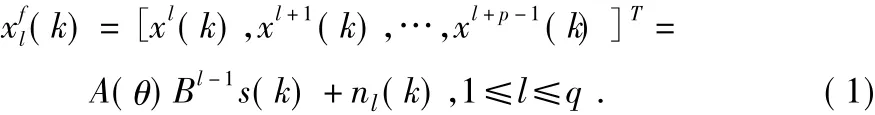
式中:k表示第k次快拍，

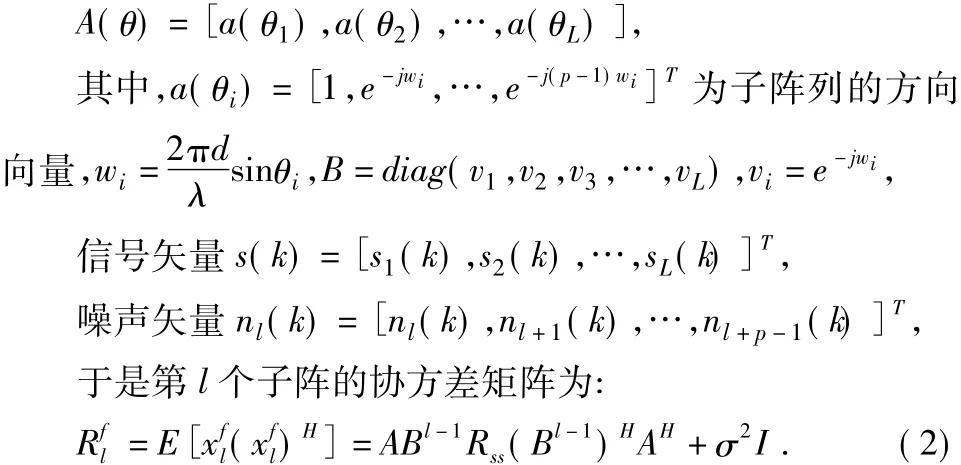
其中Rss为信号的协方差矩阵。

步骤3:计算每个子阵列的协方差矩阵，再将协方差矩阵取平均，作为前向平滑矩阵:

步骤4:对前向平滑矩阵进行特征分解

式中:U为特征矢量矩阵，Σ =diag（λ1，λ2，…，λp），将Rf的特征值按从大到小排序，则有:

xx

λ1≥λ2…≥λL≥λL+1=… = λP= σ2n，前L个大的特征值对应的特征向量张成信号子空间Us，相等的P-L个小的特征值对应的特征向量张成噪声子空间Un。

构造MUSIC空间谱函数Un:

空间谱的波峰对应的角度就是波达方向。

2 仿真分析

相干信号环境下的仿真分析:在图1所示的均匀直线阵列中，设定阵元数M=8，阵元间距为半波长，信源数L=3;三个信号的来波方向分别为 10°，35°和 60°，其中 10°，35°两个方向的信号是相干的;噪声是均值为0，方差为1的加性高斯白噪声;快拍数为1024，信噪比为15dB。在此情况下，分别采用经典MUSIC算法和子阵数q=3，子阵阵元数p=6的前向平滑MUSIC算法对波达方向进行估计，Matlab仿真结果如图2所示。

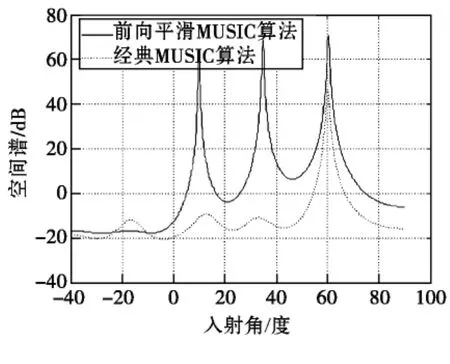
图2 两种MUSIC算法仿真比较

从图2可以看出，在处理相干信号源时，经典MUSIC算法失效，不能准确估计出10°，35°两个相干信号的来波方向;而利用前向平滑MUSIC算法，三个信号均被清晰地分辨出来。由此说明，前向平滑MUSIC算法能很好地估计出相干信号的波达方向。

3 前向平滑MUSIC算法的FPGA设计

前向平滑MUSIC算法的FPGA设计［6］可以分为以下三步:计算采样协方差矩阵，对协方差矩阵进行特征分解（EVD）和谱峰搜索（如图3）。

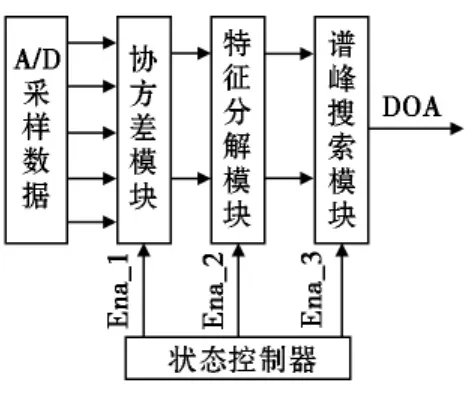
图3 MUSIC算法FPGA设计

下面以八阵元均匀直线阵为模型，介绍前向平滑MUSIC算法的FPGA设计。

3.1 协方差模块的实现

将均匀直线阵划分为子阵阵元数为6，子阵数为3的模型，子阵的协方差矩阵元素的表达式为:

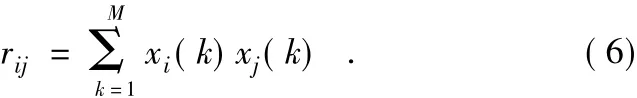
式中:M为快拍数，k表示第k次快拍，xi表示公式（3）中xf

l（k）的第i个元素，rij表示协方差矩阵第i行第j列的元素。

协方差矩阵模块为一个乘法累加器，需要同时计算28个上三角矩阵元素和8个对角元素，可设计一个并行的乘法累加器使得每个时钟周期都可以同时进行36次相乘累加计算。

对求出的协方差矩阵进行酉变换［7］，将复数域转化为实数域，降低其运算复杂度，酉变换公式为Re{Qxfl（k）QH}

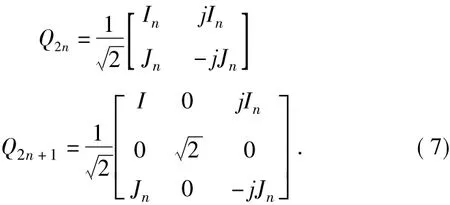
其中In为n阶单位矩阵，Jn为n阶交换矩阵。

对酉变换之后的矩阵进行求和平均，输出协方差矩阵用于特征分解，设计如图4。

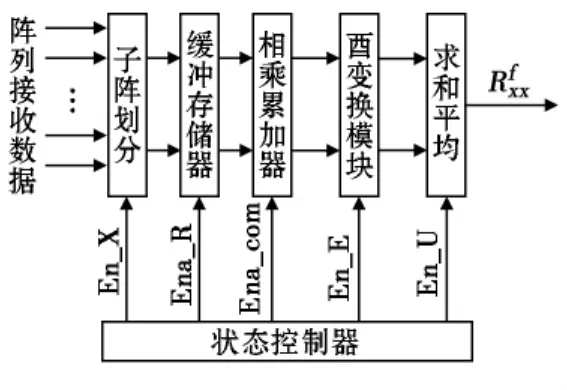
图4 协方差模块结构框图

3.2 特征分解模块的硬件实现

该模块采用Jacobi算法［8］完成对协方差矩阵的特征分解，如图5。

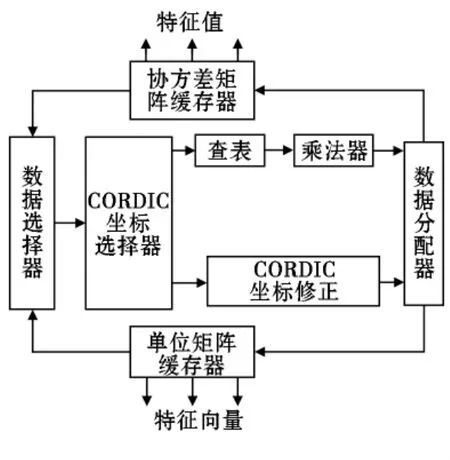
图5 EVD模块设计框图

3.2.1 矩阵缓存器、数据选择器和数据分配器

在特征分解迭代过程中，矩阵缓存器负责缓存和更新协方差矩阵和单位矩阵的元素。

数据选择器在迭代过程中对Jacobi算法进行控制，负责控制缓存器中数据的写入和写出。

3.2.2 计算模块

用 CORDIC［9］坐标旋转和 Jacobi［10］迭代算法，将协方差矩阵对角化。

Jacobi算法的流程如下:

（1）CORDIC反正切模块计算旋转角

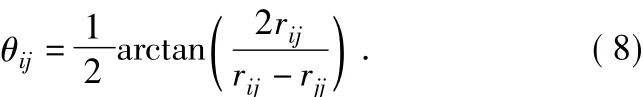
（2）CORDIC旋转模块计算坐标旋转

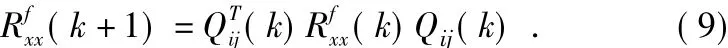
式中:k为迭代次数，Qij（k）为第k次迭代的旋转矩阵，Rfxx（1）=Rfxx。

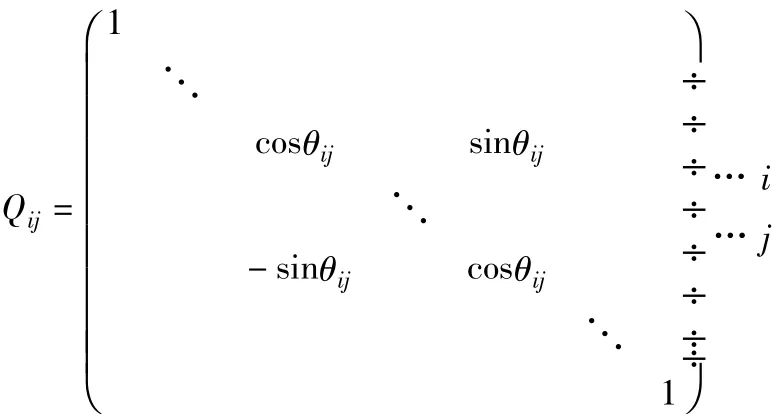
（3）迭代过程中，按照如下顺序进行扫描:r12→r13→…→r18→r23→…r28→…→r78在单次迭代后，矩阵Rfxx的上三角元素rij约等于0。若所有的上三角元素都完成“扫描”，则这样的过程称为一次“清扫”。在n1次“清扫”后，非对角元素近似为0，对称矩阵Rfxx转换为对角矩阵Rf xx（n1），其对角元素即为特征值。

（4）用同样的旋转矩阵对单位矩阵E进行旋转，E（k+1）=QTijE（k）Qij，E（1）=E，同样经过n1次迭代之后，得到矩阵E（n1），矩阵E（n1）的列矢量就是特征向量，对应于Rfxx（n1）对角线上同一列的特征值。

3.3 谱峰搜索模块

该模块利用特征分解模块输出的特征值和特征向量，进行谱峰搜索，求出波达方向，如图6。

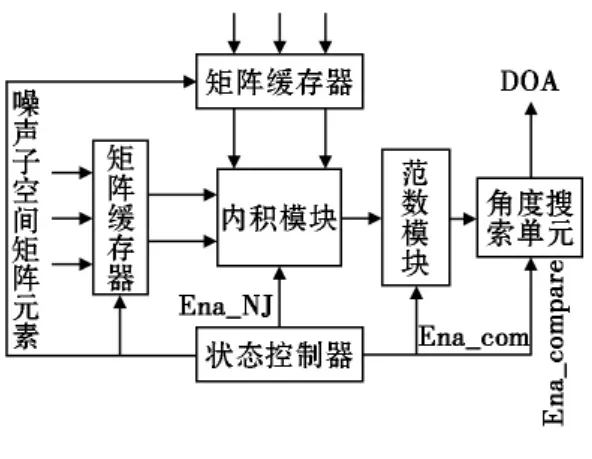
图6 谱峰搜索模块

矩阵缓存器，用于将方向向量保存在ROM中。对于本文使用的均匀线阵，其角度的搜索范围是-90°～90°。设定搜索步长为1°，所有的a（θi）值可以预先计算好并写入ROM芯片内，再通过内积模块和范数模块计算AH（θ）UnUHnA（θ），得到180个谱函数值;最后通过角度搜索单元对180个数据进行比较，得出最小值，其对应的角度就是波达方向。

4 结束语

本文研究了一种用于处理相干信号波达方向的改进型MUSIC算法，并通过matlab仿真与经典MUSIC算法进行比较，分析其性能。利用 FPGA并行计算［11］的优点，研究了FPGA实现前向平滑MUSIC算法的原理，对实际工程应用具有一定意义。

［1］黄少杰.浅谈智能天线技术及其在3G中的应用［J］.中国电子商务，2011，（8）:37-37.

［2］肖先赐.现代谱估计——原理与应用［M］.哈尔滨:哈尔滨工业大学出版社，1991.

［3］Schmidt R O.Multiple Emitter Location and Signal Parameter Estimation［J］.IEEE Trans.on AP，1986.3.AP-34:276-280.

［4］吴国庆，陈善继.基于解相干的MUSIC算法估计性能分析［J］.现代电子技术，2011，34（7）:94-96.

［5］Qing Chen，Ruolun Liu.On the Explanation of Spatial Smoothing in MUSIC Algorithm for Coherent Sources［C］.International Conference on Information Science and Technology，2011，3:699-702.

［6］郑洪.空间谱估计算法的高速实现［D］.成都:电子科技大学电子工程学院，2004.

［7］何劲，陈建文，刘中.利用空时相关矩阵酉变换估计达波方向［J］.系统工程与电子技术，2005，5（27）:811-813.

［8］刘婷婷，刘俊卿，张健楠.基于Jacobi方法的Hermitian矩阵特征分解算法［J］.电子科技，2010，23（12）:60-61.

［9］牛晨晓，赵忠，聂聪.一种CORDIC算法的FPGA实现［J］.计算机技术与发展，2011，6（21）:16-19.

［10］Wang Tao，Wei Ping.Hardware Efficient Architectures of Improved Jacobi Method to Solve the Eigen Problem［C］.2010 2nd international conference 011 computer engineering and technology，ICCET，2010（6）:22-25.

［11］陈景良.并行算法的设计与分析［M］.北京:高等教育出版社，1994.