钢筋混凝土介质爆破开裂过程的数值模拟

杨 丽，曾宪刚，丙孟芬，杜晓宁

(1.沈阳理工大学装备工程学院，辽宁沈阳110159;2.辽沈工业集团有限公司，辽宁沈阳110045;3.中国核电工程有限公司，河北石家庄050019)

随着科学技术的发展，对钢筋混凝土的抗爆性能和结构强度提出了更高要求，进而需对钢筋混凝土的爆破开裂问题进行研究，以便找到提高钢筋混凝土抗爆性能和结构强度的有效途径。钢筋混凝土有限元分析是结合钢筋混凝土特点发展起来的一种弹塑性分析方法。钢筋和混凝土之所以能组合起来共同工作，主要是两者之间存在粘结作用，但粘结力与其相对变形的关系很复杂，影响因素很多［1－2］。目前主要用线弹性理论分析钢筋混凝土结构的应力或内力，以极限状态的设计方法确定构件的承载能力、刚度和抗裂性。这种设计往往基于大量试验数据上的经验公式，虽然这些经验公式能反映钢筋混凝土构件的非弹性性能，对常规设计来说简便易行，但在使用上还有局限性，也缺乏系统的理论支持［3］。

本文以钢筋混凝土破坏的基本理论为基础，利用软件ANSYS/LS-DYNA对钢筋混凝土爆破开裂过程进行模拟分析，通过建立数学模型，模拟裂缝的形成和扩展过程，研究爆炸应力波传播对介质的破坏过程。通过对爆破开裂效果对比分析可知:钢筋混凝土爆破在应力波作用下，药包外围逐渐形成压缩区、破裂区，裂纹沿切向扩展，沿径向延伸。研究结果可为结构的极限承载能力和可靠度评估提供依据，找出结构的薄弱部位和环节，有利于对钢筋混凝土建筑进行优化设计。

1 钢筋混凝土结构的理论基础［1］

钢筋和混凝土两种材料结合在一起，混凝土主要承受压应力，钢筋主要承受拉应力。炸药爆炸产生的应力波为三种波，即冲击波、压应力波和地震波。根据这三种波的破坏特点，考虑混凝土材料的抗压受载远大于抗拉受载，破坏开裂主要是由压应力波衍生的拉应力波作用造成。图1所示为介质在应力波作用下形成的裂隙。破坏符合钢筋混凝土破坏机理的最大拉应力理论和最大伸长线应变理论［4－5］。

图1 介质在应力波作用下形成的裂隙

1.1 最大拉应力理论

该理论又称第一强度理论，这一理论认为最大拉应力是引起断裂的主要因素。即认为无论是什么应力状态，只要最大拉应力达到与材料性质有关的某一极限值，材料即发生断裂。既然最大拉应力的极限值与应力状态无关，于是就可用单向应力状态确定这一极限值。

1.2 最大伸长线应变理论

该理论又称第二强度理论，这一理论认为最大伸长线应变是引起断裂的主要因素。即无论什么应力状态，只要最大伸长线应变达到与材料性质有关的某一极限值，材料即发生断裂。

由上述理论可得:由于裂纹的产生，棱角附近的单元体内的应力得以释放，应力波的外轮廓线形状也因此发生改变，如图2所示。

图2 应力波外轮廓线

2 钢筋混凝土的整体式模型［1］

钢筋混凝土有限元分析的整体式模型是将钢筋弥散于整个单元中，并把单元视为连续均匀材料，仍用虚功原理得出的关系式

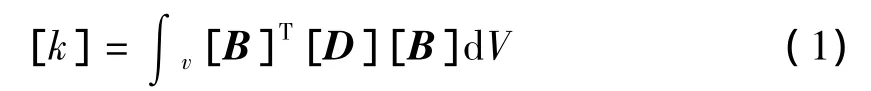
求单元刚度矩阵。其中的弹性矩阵［D］由两部分组成，即

式中［Dc］、［Ds］分别为混凝土、钢筋的应力应变矩阵。［Dc］在开裂前可按各向同性的一般均质体计算，具体表达式为

式中

Ec为混凝土即时割线模量，它随应力状态的变化而变化;v为泊松比。

在混凝土开裂后，这一关系矩阵必须修改。如果在单元中某点的主应力按代数值大小排列为σ1≥σ2≥σ3，其中最大主应力σ1大于混凝土的抗拉强度时，则认为产生了裂缝，并且假定裂缝方向垂直于σ1方向。开裂后，最大主应力将被释放而应力重新分布，应力-应变关系矩阵中刚度系数变为零，其应力应变关系矩阵可修改为

式中，d11、d12、…、d66与式(3)求法相同;η 为残留抗剪系数，这是考虑到虽有裂缝，但由于咬合、暗销等作用，混凝土尚可保持部分抗剪能力。若η=1，则和未开裂时一样，即抗剪能力不受开裂的影响;若η=0，则混凝土的抗剪能力全部丧失。故应有0≤η≤1，一般取η=0.3～0.6进行计算。

式(4)中的关系矩阵是按最大主应力方向为坐标轴方向而建立起来的，求单元刚度矩阵时，还要转到总体坐标系中。假设最大主应力方向与整体坐标系x轴之间的夹角为θ(顺时针为正，反之为负)，C=cosθ，S=sinθ，则可利用下列坐标转换矩阵转到整体坐标系中。

式中，［D'c］为在局部坐标系中应力应变关系矩阵，［R］为坐标转换矩阵，具体表达形式为

钢筋的应力-应变关系矩阵［Ds］，可按前述的理想弹塑性模型计算，屈服前按线弹性计算，屈服后取弹性模量E=0。

3 数值模拟的计算过程

3.1 问题描述

对一堵钢筋混凝土墙实施爆破，该混凝土墙的前后两面均为自由面，其四周均受固定端约束，在该墙体的中心处打一通孔放置炸药。基于问题的对称性，为节省计算时间，只需建立1/4模型，并采用方形装药结构。钢筋混凝土内方形药包爆炸结构示意图如图3所示。

图3 钢筋混凝土内方形药包爆炸结构示意图

3.2 状态方程［6］

在高能炸药材料关键字段后添加*EOS_JWL关键字段，用以描述爆生气体的状态。LS-DYNA程序描述高能炸药爆轰产物压力-体积关系采用JWL状态方程。高能炸药爆轰产物的单元压力P由状态方程求得，JWL状态方程的P-V关系如下

式中:V为相对体积;E0为初始内能密度;参数A、B、R1、R2、w 为试验确定的常数。

3.3 参数设计

(1)炸药参数的选择和设计

对于装药密度为1.2g/cm3的TNT炸药，各相关参数分别取值如下:

A=741GPa，B=18GPa，w=0.35，R1=5.56，R2=1.65，E0=3.6 ×109J/m3。

具体参数如表1所示。

(2)钢筋混凝土参数的选择和设计

具体数据参数如表2所示。

4 计算结果和分析

用LS-PREPOST对结果文件进行可视化处理，动画显示。动画效果如图4所示。图4中分别列出12个时刻的钢筋混凝土爆破开裂效果图形。

表1 关键字*EOS_JWL参数

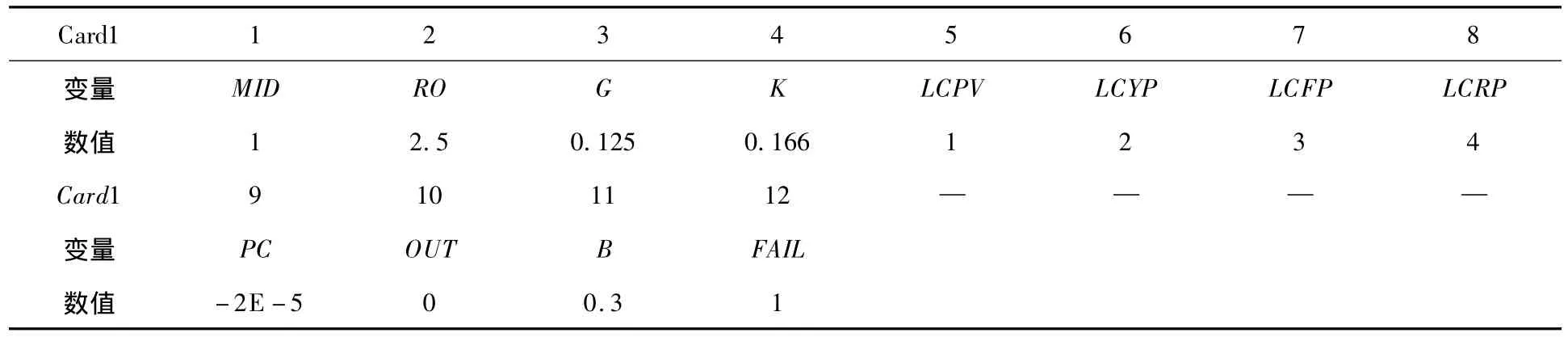
表2 关键字*MAT_SOIL_CONCRETE数据格式

图4 钢筋混凝土爆炸开裂模拟过程

由图4可得:

(1)t=0μs时，即炸药引爆时刻，应力均匀分布在炸药外围表面，即将向钢筋混凝土传递。由于药包形状为方形，因此钢筋混凝土内存在尖锐角度(药包的四个棱角位置)，造成应力集中。t=1.9054μs时，裂纹起始于应力集中处。模拟结果与图2所示的理论结果相吻合。随着应力波向外传播，应力逐渐均匀向外分布，与此同时，炸药爆炸所产生的气体物质向外膨胀，并且形成向外扩张的界面。t=8.9491μs时的图像已能见到有界面形成。

(2)在爆炸发生的数微秒内，爆轰压力急剧增高并在药包周围的钢筋混凝土中激起冲击波，其强度远远超过钢筋混凝土的抗压强度极限。在冲击波作用下，钢筋混凝土部分受到粉碎性破坏，形成粉碎区;部分被压缩，装药孔周围形成较为坚实的压实层。

(3)在粉碎区形成的同时，钢筋混凝土中的冲击波衰减成压应力波。由t=19.974μs时的图像可看到，压应力波继续向外围传播。在应力波作用下，钢筋混凝土在径向产生压应力和压缩变形，切向产生拉应力和拉伸变形。由于钢筋混凝土的抗拉强度远低于抗压强度，当切向拉应力大于钢筋混凝土的抗拉强度时，该处钢筋混凝土被拉断，形成径向裂隙。

(4)随着径向裂纹的形成，作用在钢筋混凝土上的压力迅速下降，药包周围的钢筋混凝土随即释放出在压缩过程中积蓄的弹性变形能，形成与压应力波作用方向相反的拉应力，使钢筋混凝土的质点产生反方向径向运动。当径向拉应力大于钢筋混凝土的抗拉强度时，该处钢筋混凝土即被拉断，形成环向裂隙。破裂效果如图5所示。

图5 破裂效果图

(5)从 t=25.998μs至t=31.982μs的图像中可看出，裂纹进一步沿径向扩展，且新扩展的裂纹小于前一应力波作用所导致的裂纹。产生这一现象的主要原因在于导致前一次裂缝产生的应力波能量一部分被裂纹所吸收，使得能量部分丢失，因而开裂程度有所减弱。

(6)从t=480.99μs时的显示图像中看到爆炸物质界面散开后药包周围的孔壁破损情况，孔壁周围仍有应力集中存在，其能量已不能使钢筋混凝土产生裂缝。

(7)从t=480.99μs时的显示图像中可知，粉碎区半径是药包半径的3.25倍，这主要是因为钢筋混凝土材料选取的是整体式模型，其抗压强度略低于普通岩石。

(8)从图6不同方向应力波的变化曲线可知，在t=32μs之后，某单元体所受最大拉应力值与最大压应力值大致相同，不再有剧烈波动。其主要原因在于t=32μs之后，爆炸作用下的钢筋混凝土不再产生新的裂纹区，但是压应力波的传播并未停止，这一点可在开裂过程得到印证，且单元体的弹性变形能也将即时释放，形成与压应力波作用方向相反的拉应力，因此才会使X、Z向应力曲线上下波动且峰值大致相同。此单元体将继续传播应力波，直到爆炸演示的终止时间，其应力线仍然在上下波动，即为由应力波衰减形成的地震波。

图6 X、Z方向应力波的变化曲线

5 结论

(1)对钢筋混凝土的爆破开裂数值模拟，通过仿真结果的理论校验、对比分析论证，对裂纹的产生扩展影响因素、形成原因进行了多方面分析，结果基本符合实际。

(2)实际的钢筋混凝土爆破过程中，在药包的外围会依次形成压缩区、破裂区。裂纹在应力波作用下沿切向扩展，沿径向延伸且贯穿压缩区和破裂区。模拟结果与钢筋混凝土破坏理论基本吻合。

［1］袁志芬.钢筋混凝土结构非线性有限元分析［D］.西安:西安农林科技大学，2001.

［2］谢里阳，吴克勤.裂纹梁动力学仿真的有限元模型［J］.东北大学学报，2008，29(5):714 －716.

［3］孙金山，卢文波.框架结构建筑物拆除爆破模拟技术研究［J］.工程爆破，2004，10(4):1 －3.

［4］杨军，陈鹏万，胡刚.现代爆破技术［M］.北京:北京理工大学出版社，2005:17－22.

［5］何春林，邢静忠.ANSYS对钢筋混凝土结构弹塑性问题的仿真研究［J］.煤炭工程，2007(4):80－82.

［6］LS-DYNA KEYWORD USE’SMANUAL［Z］.California Live more Software Technology Corporation，2003.