天津—北京高分辨地震折射剖面初至波走时成像①
贾宇鹏,王夫运,田晓峰,段永红,莘海亮,刘宝峰
(1.中国地震局兰州地震研究所,甘肃 兰州 730000;2.中国地震局地球物理勘探中心,河南 郑州 450002)
0 引言
精细的地壳速度结构研究有助于了解基底和莫霍面形态,结合地质情况可对活动断层等作出合理的解释,为研究地震的孕育环境和发生机理提供科学的依据。首都圈地区位于NE向的太行山隆起,EW向的燕山隆起和华北平原的交汇之处,地质情况复杂。已有众多学者对该区域做了大量研究工作,得到了很多成果。王夫运等[1]利用三维不分块层析成像技术得到北京地区P波S波慢度图和波速比图,发现慢度和速度比的分布有呈NE向和NW向展布的特征。段永红等[2]利用华北地区的30多条探测剖面得到了上部地壳的三维速度结构,结果表明华北盆地由两个大的断陷带中间夹一个隆起组成,两个大的断陷带又分为几个小的断陷盆地,区域内的断层多为铲式正断层,结晶基底深度变化较大。嘉世旭等[3-4]利用该高分辨剖面数据研究了华北东部裂陷盆地与燕山隆起区的地壳结构和构造耦合,给出了地壳速度模型和断裂的位置,结果表明剖面西侧燕山隆起区地壳结构高速稳定但东侧裂陷盆地低速松散。王帅军等[5]得到了该剖面的二维地壳速度结构,可以清楚看到基底面、壳内的反射界面和莫霍面的位置和形态。刘保全等[6]用深地震反射剖面探测了北京地区的地壳精细结构。
为了进一步探究该地区的精细地壳结构和活动断层构造环境,2006年初中国地震局地球物理勘探中心在首都圈地区完成了一条高分辨折射地震探测剖面,取得了优质的爆破地震资料。本文使用Colin Zelt的正则化反演方法[7-8],对反映该区域上地壳结构的Pg波走时数据进行成像,研究天津塘沽—北京顺义高分辨折射探测剖面的上地壳二维精细速度结构,并探讨该地区的潜伏断层。
1 观测系统和数据
高分辨地震折射剖面东起渤海之滨的天津塘沽,通过华北坳陷区北部,到达燕山台褶带南部边缘的北京东北郊顺义区,剖面全长185km。布设观测点267个,最小观测点距0.35km,最大观测点距0.70km,平均观测点距0.51km;炮点18个,平均炮间距12.15km。构成了较为完整的多重追逐和多重相遇观测系统。位于测线东南部的华北坳陷区为新生代强烈坳陷区,其构造及块体延伸方向大致为NNE-NE向;位于测线西北部的是北京平原西北部,测线最西北端到达燕山褶皱带南端(图1)。
采用全部18炮所拾取1 454个Pg波走时数据反演上地壳精细速度结构。如图2(a)、2(b)、2(c)分别为剖面西北端桩号为297(第18炮),中间桩号225(第10炮)和东南端桩号118(第1炮)炮点的折合速度记录图。Pg波到时主要受基底速度和其上的沉积盖层厚度及盖层速度的影响。剖面西北段(图2(a))的北京平原区由于靠近燕山隆起的南缘,沉积盖层较薄,基底速度较高,Pg波折合到时约1~2s;而剖面中段(图2(b))和东南段(图2(c))的华北平原区由于受到冀中坳陷和黄骅坳陷沉积层的影响,Pg波的折合到时约1~4s。
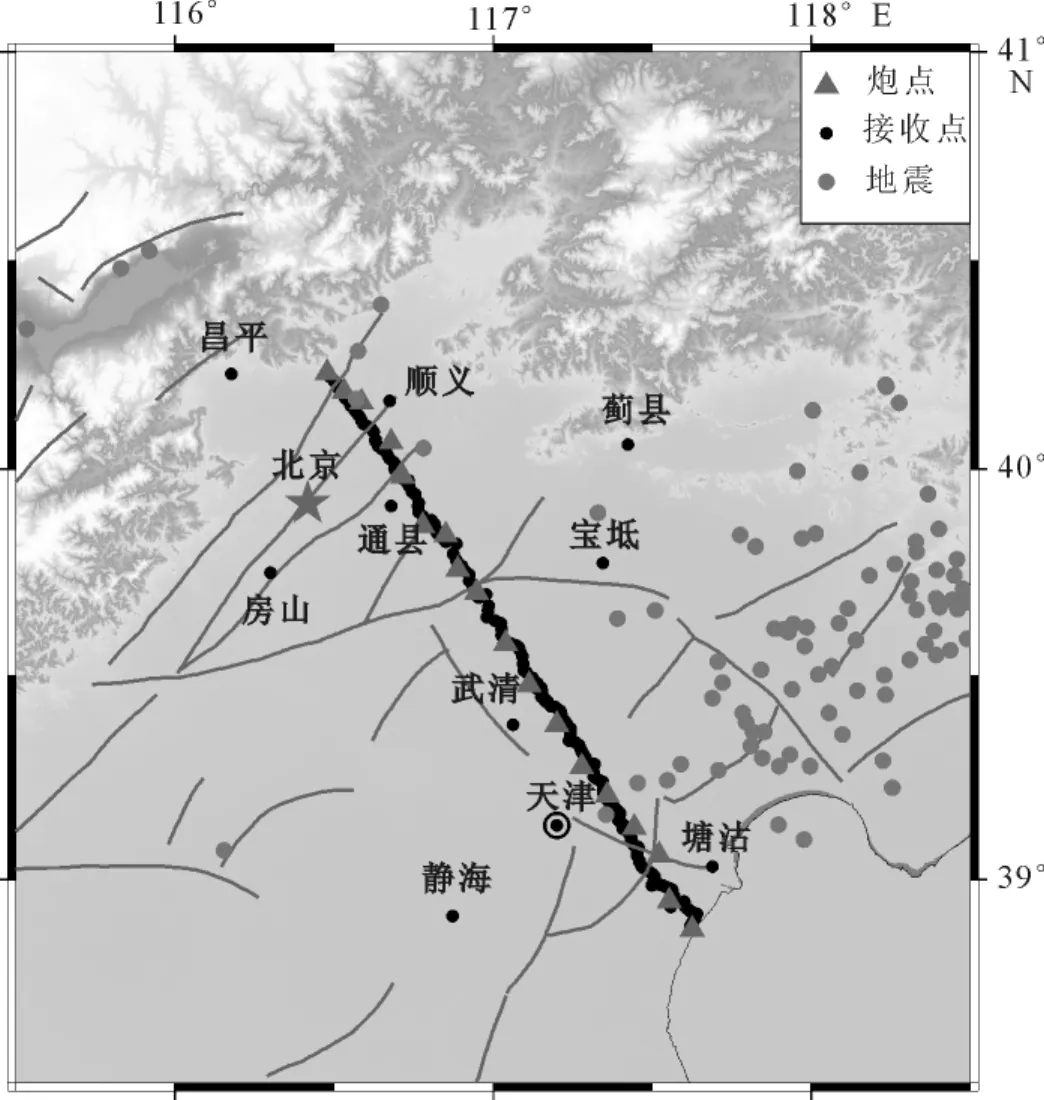
图1 天津—北京高分辨折射/反射测线位置图Fig.1 Location Map of High Resolution Refraction/Wideangle-reflection Profile from Tianjin to Beijing.
由于沿剖面地质构造不同,加之采集数据时的一些因素,数据在不同地段的拾取误差就有所不同。可以看出,图2三张记录图在炮点附近约30km内记录的信噪比还是不错的,桩号297的炮点要好于桩号118的炮点。通过分析全部18炮的数据记录图,发现Pg的信噪比在燕山南缘过渡带(300~245)较好,追踪较远,在冀中坳陷(245~180)和黄骅拗陷(140~115)一般,追踪较短。第1,2,3,4炮Pg在SE方向追踪到侧线端点,NW方向追踪到冀中坳陷东南端(桩号180)附近;第5,6,7炮SE方向受黄骅拗陷的影响,追踪较短,到达桩号140附近,NW方向能穿越大半个冀中坳陷,追踪到桩号220附近;冀中坳陷内部的第8,9,10炮Pg可完全追踪覆盖冀中坳陷;第11~18炮东南方向追踪到桩号190附近,基本穿过了冀中坳陷,NW方向由于是燕山南缘过渡带,可清晰追踪到剖面的西北端点。
2 速度成像
2.1 成像原理
传统上采用有限差分求解程函方程的正演算法,已有较多文献进行讨论[9-14]。对于反演成像方法,John Hole在1992年提出了将走时残差分布在整个射线上的反投影算法,由于反投影算法无需进行矩阵计算,反演效率很高[9]。Toomey指出,反投影算法将残差分布在整条射线上进行计算,对于射线密集的高速区域会带来较大计算误差[12],Colin Zelt提出了修正的反投影算法以避免高速区射线集中带来的误差累积[7]。
本文采用Colin Zelt的正则化反演方法(FAST)[7]对剖面的上地壳速度结构进行精细成像。该方法在解病态方程组时在数据之外引入一些约束条件去处理解的欠定部分或防止数据过度拟合,这些约束条件通常是对解的复杂性的与约束性措施,如成像中的平滑度控制。因此,正则化过程在一定程度上可视为反演走时曲线而非拟合单点走时[9]。由此,可构造一个包含速度模型平滑度和数据拟合度的目标函数[7-8]:

其中m是模型矢量;δt是数据残差;Cd是数据协方差矩阵;Ch和Cv分别是水平和垂向平滑度矩阵;λ是数据拟合与模型平滑度协调因子;sz是水平与垂向平滑度权重因子。于是,每一次的线性迭代问题可归结为求解一个δm,使得目标函数最小[7]:
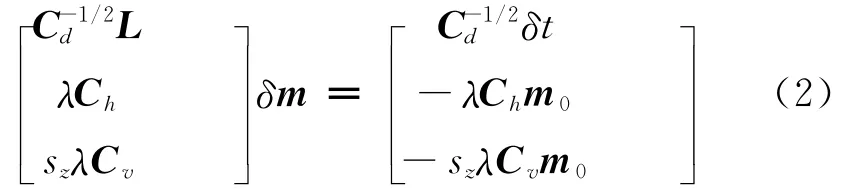
式中L是目标函数偏导数矩阵;m0是当前模型;δm是待求模型扰动,新模型矢量m=m0+δm。方程(2)可用LSQR算法求解。
采用横向和纵向不同宽度的网格大小,同时合理选取正则化因子可以对剖面上部分无射线覆盖区可以较好地给出合理的平滑解,得出整个研究区在横向和纵向较合理的最小格点最平滑解[7]。
2.2 成像过程
2.2.1 初始模型
初始速度模型的选取与研究区域的地质构造密切相关,该区域坳陷和隆起区相间,构造复杂。为了得到可靠的反演结果,选取了四个十分不同的初始模型进行试验,如图3。

图3 一维初始速度模型Fig.3 1DStarting velocity models.
2.2.2 正演、反演参数
初至波成像方法的横向分辨很大程度取决于观测点距和爆破点的密集程度,而纵向分辨除此之外还取决于研究区域壳内的速度梯度。由于剖面是高分辨的观测系统,最小观测点距达到0.35km,最大观测点距0.70km,平均观测点距0.51km,平均炮间距12.15km,所以正演模型采用较密集0.25km×0.25km的格点间隔。考虑到反演单元格横向宽度要尽可能接近观测点距和纵向上该区域的沉积盆地导致从地表到基底有较大速度梯度,因此反演采用0.50km×0.25km的单元格。反演迭代次数可以由χ2到达1附近而且随迭代变化很小而确定。经试验迭代20次就能够达到此要求,所以选取20次迭代。根据以往的经验,水平与垂向平滑权重因子Sz暂定为0.20。由此来讨论初始模型对反演结果的影响。

图4 不同初始模型得到的速度图Fig.4 Testing of different starting velocity models.
由表1可以看出,使用十分不同的初始速度模型进行反演计算,初始均方根残差区别很大,但是经过20次迭代后,最终均方根残差都达到65ms左右。图4中,两条黑线为3.5km/s和4.5km/s的速度等值线,较密集的三条白色线为5.8km/s,5.9 km/s,6.0km/s的速度等值线。可以看出(a)速度图和其余三个(b),(c),(d)速度图有一定的差别,但是差别主要体现在射线覆盖不够的底部区域,四张速度图的上部区域大致形态还是相似的。这说明反演结果对初始模型的依赖性不大,走时数据起决定性作用。说明该方法(FAST)比较可靠,可以用来处理高分辨观测系统的资料。

图5 不同平滑权重因子Sz得到的速度图Fig.5 Testing of different vertical versus horizontal model smoothness factor Sz.
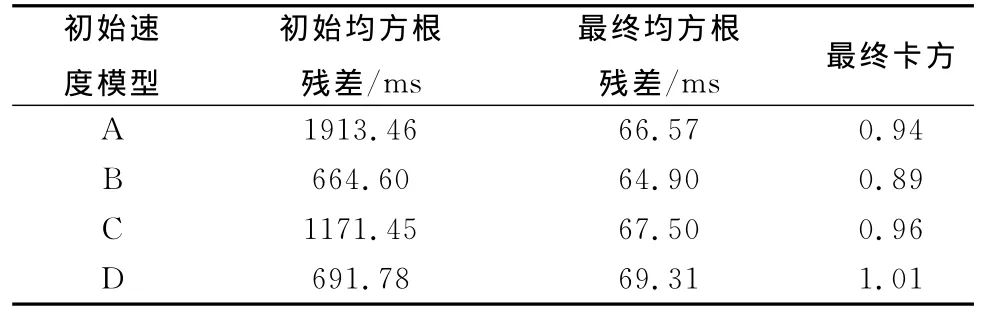
表1 不同初始模型对结果的影响
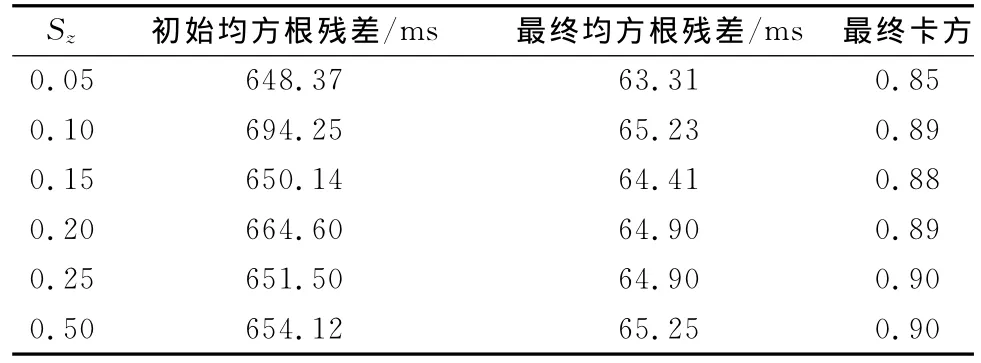
表2 不同平滑权重因子Sz对结果的影响
参考已有的研究成果,依据该地区地壳模型的先验信息,从中选取初始速度模型B来进一步讨论水平与垂向平滑权重因子Sz对反演结果的影响,反演依然迭代20次。
表2中不同的Sz值对模型的初始、最终均方根残差影响比较抽象,而图5就比较直观了。可以明显的看出Sz对两条黑线为3.5km/s和4.5km/s的速度等值线影响较小,但对可能反映基底形态的三条白色线5.8km/s,5.9km/s,6.0km/s的速度等值线的影响较大。考虑到射线的覆盖密集程度及未采样区域,每一组闭合白线的上部更能够反映基底形态。参考已有的研究成果,最终选取Sz为0.20。
2.2.3 成像结果
图6(a)为初始速度模型B和Sz为0.20的最终P波速度模型图,上下两个图分别为深度方向扩大比例为4和1。其初始均方根残差为664.60ms,最终均方根残差达到64.90ms。图中五角星为爆炮点,深色虚线为潜伏断裂,浅色虚线为地层尖灭线。
2.3 检测板分析
采用检测板方法对最终模型(图6(a))的分辨进行评估。在最终速度模型加入5%的速度扰动后,使用该速度模型作为检测板输入模型,由此产生正演数据并加入5%的噪音进行反演恢复,经过20次迭代得到检测板恢复模型。图7是网格大小为2.5km×0.5km,5km×1km,10km×2km和20 km×5km的恢复模型。
可以看出,20km×5km和10km×2km网格的测试在整个模型上恢复的很好,分辨完全可以达到网格的大小;5km×1km的网格能较好的恢复0~4km深度;2.5km×0.5km的网格在模型的浅部都不能恢复,恢复情况不好。图7(b)显示模型分辨在燕山南缘过渡带要优于几个拗陷的内部。
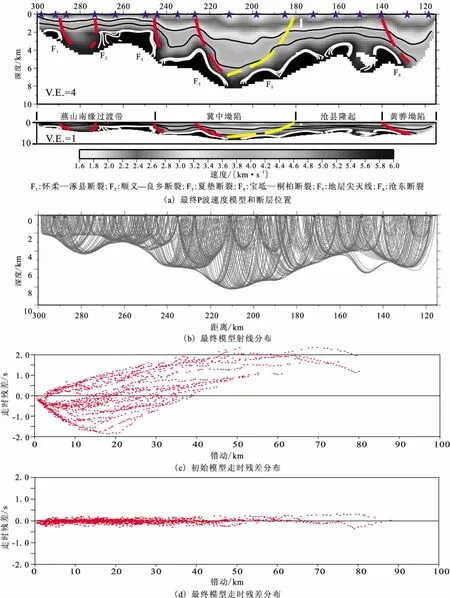
图6 最终速度模型及射线和残差分布Fig.6 The final velocity and distribution of ray paths,traveling time residues.
3 结论和讨论
图6(a)中,上地壳速度分层明显,基本反映出了该地区不同构造单元的沉积厚度和基底形态。白垩纪沉积,第三系沉积和基底的埋深极为相似,这说明该地区受到第三系以来的地壳运动的影响较大。

图7 不同网格大小的检测板试验恢复模型Fig.7 Traveltime checkboard resolution tests using difference grid sizes.
两条黑线为3.5km/s和4.5km/s的速度等值线,可能分别对应于第三系以来沉积层厚度和早第三系与白垩纪沉积岩分界,较密集的三条白色线为5.8km/s,5.9km/s,6.0km/s的速度等值线,结合图6(b)的射线在基底为滑行波,或许反映了沿剖面基底界面的大致形态。基底最浅处约2km,最深处约达到8km。剖面桩号290~275的北京凹陷基底埋深明显较深;剖面桩号275~245通县凸起区基底埋深约为2km;剖面桩号245~225的大厂凹陷基底埋深约5km;剖面桩号225~180的武清凹陷,基底埋深约4~8km;剖面桩号180~140的沧县隆起基地埋深约4km;剖面桩号140~115的黄骅拗陷,基底埋深约6km。
断裂和底层尖灭线一般出现于速度梯度变化较大的界面,参考其他研究所给出的断裂和底层尖灭线位置[1-5,15],结合本研究所得到的天津—北京的高分辨地震折射剖面的上地壳精细速度结构(图6(a)),给出了该地区的潜伏断层与地层尖灭线的大致位置。F1怀柔—涿县断裂和F2顺义良乡断裂位于北京凹陷、通县突起和大厂凹陷的交界转换区域,这里速度梯度变化很大;F3夏埑断裂和F4宝坻铜川断裂依据为在3.5km/s和4.5km/s的速度等值线左右两边和沿着代表基底形态的白色的速度等值线迅速下降;F5底层尖灭线在地表两端分别的速度为1.6km/s和2.3km/s,速度差异较大,在3.5 km/s和4.5km/s的速度等值线左右两边和基底的速度等值线处有明显变化,也可认为F5是沧东断裂;F6沧东断裂依据为从地表到基底速度明显变化的区域。
图6(b)最终模型射线追踪图可以看出,射线分布在地表极为密集,基底以上较为密集,对所研究区域上地壳有较好覆盖。在基底处,射线表现为滑行波,在此图中有明显表现。图中一共1 454根射线,射线完全密集覆盖所研究区域,成像结果可靠。
图6(c)和(d)为初始和最终走时残差。经过20次迭代后,走时残差分布迅速减少到约200ms以下,这说明最终模型数据与观测数据获得了较好的拟合。
总之,成像结果的精细程度与可靠性取决于观测系统是否为高分辨,数据质量较好和使用合适的成像方法。通过上文的分析,这三方面都达到要求。在使用Colin Zelt正则化反演方法(FAST)的过程中,分析讨论了不同初始模型和参数变化对反演结果的影响,并采用检测板方法对最终模型的分辨进行评估。因此可以说,本文中给出的天津-北京剖面的地壳上地壳精细速度模型(图6(a))是高分辨的,并且是比较可靠的。
致谢:感谢天津城市活断层试验探测项目的野外采集和室内处理人员的辛勤劳动。感谢Colin Zelt教授提供的FAST软件包。
[1] 王夫运,张先康,陈棋福,等.北京地区上地壳三维细结构层析成像[J].地球物理学报,2005,48(2):359-366.
[2] 段永红,张先康,方盛明.华北地区上部地壳结构的三维有限差分层析成像[J].地球物理学报,2002,45(3):362-369.
[3] 嘉世旭,张成科,赵金仁,等.华北东北部裂陷盆地与燕山隆起地壳结构[J].地球物理学报,2009,52(1):99-110.
[4] 嘉世旭,齐 诚,王夫运,等.首都圈地壳网格化三维结构[J].地球物理学报,2005,48(6):1316-1324.
[5] 王帅军,张先康,张成科,等.武清—北京—赤城二维地壳结构和构造[J].地球物理学报,2007,50(6):1769-1777.
[6] 刘保金,胡平,孟勇奇,等.北京地区地壳精细结构的深地震反射剖面探测研究[J].地球物理学报,2009,52(9):2264-2272.
[7] Colin A Zelt,P J Barton.3Dseismic refraction tomography:A comparison of two methods applied to data from the Faeroe Basin[J].J.Geophys.Res.,1998,103,7187-7210.
[8] Priyank Jaiswal,Colin A Zelt,et al.2-D traveltime and waveform inversion for improved seismic imaging:Naga Thrust and Fold Belt,India[J].Geophys.J.Int.,2008,173,642-658.
[9] Hole J A.Nonlinear High-Resolution Three-Dimensional Seismic Travel Time Tomography[J].J.Geophys.Res.,1992,97(B5):6553-6562.
[10] Vidale John.Finite-difference calculation of travel times[J].Bulletin of the Seismological Society of America,1988,78(6):2062-2076.
[11] Vidale John.Finite-difference calculation of traveltimes in three dimensions[J].Geophysics,1990:55,521-526.
[12] Toomey D R,Solomon S C,Purdy G M.Tomographic imaging of the shallow crustal structure of the East Pacific Rise at 9°30 3/4N[J].J.geophys.Res.,1994,99,24135-24157.
[13] 张元生,徐果明.联合利用走时与波形反演技术研究地壳三维速度结构(Ⅰ):理论与方法[J].西北地震学报,1998,20(2):8-15.
[14] 张元生,徐果明.联合利用走时与波形反演技术研究地壳三维速度结构(Ⅱ):应用[J].西北地震学报,1998,20(3):44-51.
[15] 王椿庸,张先康,丁志峰,等.大别造山带上部地壳结构的有限差分层析成像[J].地球物理学报.1997,40(4):459-501.

