太阳帆航天器行星际轨道转移优化算法*

钱 航,郑建华

(1.中国科学院空间科学与应用研究中心,北京100190；2.中国科学院研究生院,北京100190)

太阳帆航天器行星际轨道转移优化算法*

钱 航1,2,郑建华1

(1.中国科学院空间科学与应用研究中心,北京100190；2.中国科学院研究生院,北京100190)

研究基于遗传算法的太阳帆行星际转移轨道的全局优化问题.通过极小值原理推导了太阳帆全局优化控制律，并以太阳帆飞行时间最短为优化目标函数，运用遗传算法对发射时间、到达时间和协态变量初值进行参数优化设计.为了解决轨道转移这一多约束优化问题，在遗传算法中加入动态罚函数.在此理论基础上作了从地球同步轨道出发到火星同步轨道转移和从地球出发与火星交会两个算例，仿真结果表明了该方法在太阳帆转移轨道全局优化中的有效性.

太阳帆；全局优化；遗传算法；转移轨道；罚函数

2010年发射的日本伊卡洛斯号［1］太阳帆成功验证了太阳帆推进用于深空探测的有效性,使得太阳帆推进技术在未来空间探测任务的应用研究中成为热点.与传统化学推进方式相比,太阳帆推进利用太阳光压产生持续推力,可给航天器提供连续小推力,且自身无需携带大量燃料.虽然太阳光压很小,但持续地加速可使太阳帆最终达到传统航天器5～10倍的速度,因此适用于深空探测［2］.

太阳帆最小时间轨道转移设计的核心和难点之一是发射窗口的选取和协态变量初值的猜测［3-5］.针对这个问题,学者们发展了多种优化方法,这些方法主要可以分为两大类:间接法和直接法.间接法计算量小且能得到精确解,但由于控制曲线对初始协态变量异常敏感,同时协态变量是无物理意义的量,使得要在这样一个很小的收敛半径内猜测一个精确的初始值相当困难.直接法把优化问题转化为非线性规划问题,原理简单,收敛性好,更易于实现.

本文根据极小值原理推导了太阳帆全局优化控制律,运用遗传算法对发射时间、到达时间和协态变量初值进行参数优化设计,并采用动态罚函数法将末端约束反映到性能指标函数中,从而将最优控制问题转化为非线性规划的参数优化问题.最后,通过从地球同步轨道出发到火星同步轨道转移和从地球出发与火星交会两个算例对该算法的有效性进行了验证.

1 理想太阳帆时间最优转移轨道

1.1 运动方程

系统模型如图1所示,其中x轴指向春分点方向.本文中航天器建模为具有质量m和面积A并在动力性特性上可以视为质点的完全平整的太阳帆.定义太阳帆本体坐标系S-xbyb,其中 xb轴定义了太阳帆面的法线方向.太阳帆方向角 α(-π/2≤α≤π/2)被定义为 xb轴与照射在帆面上太阳光线的夹角.太阳帆的初始轨道和目标轨道均为太阳系行星的轨道,在此建模为日心共面圆轨道.

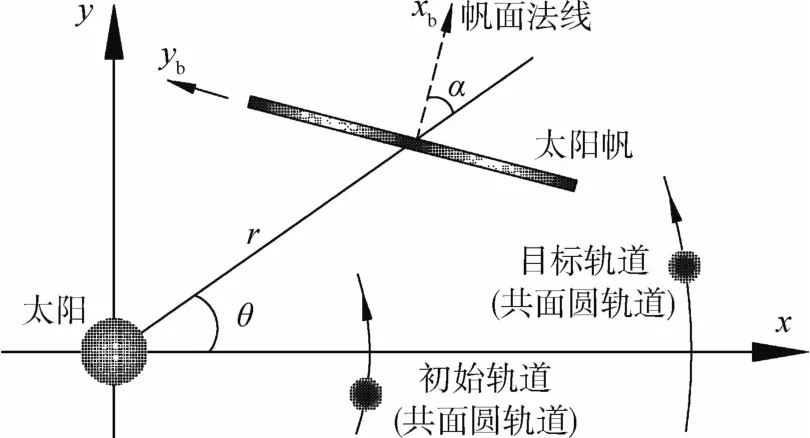
图1 系统模型Fig.1 System model

式中β为光压因子,所有变量经过无量纲化处理.

1.2 约束条件

太阳帆转移轨道的初始条件为

进入目标轨道后的终端约束条件:

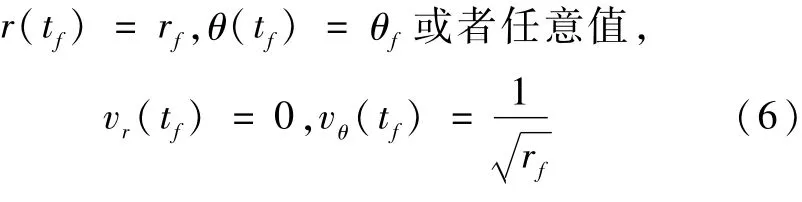
式中,t0和tf分别为出发时刻和到达时刻,r0和rf分别为初始行星和目标行星的轨道半径.对从某颗行星上出发飞往另一颗行星的任务,则要求θ(t0)=θ0和θ(tf)=θf,而对从某颗行星同步轨道出发飞往另一颗行星的同步轨道的任务,对θ(t0)和θ(tf)不作要求,θ(t0)和θ(tf)可取任意值.

对于太阳帆转移轨道优化问题,如果不加以限制,在算法迭代过程中,有时会得到转移时间tf-t0＜0的解.这显然违背了到达时刻大于出发时刻的常识,因此还必须加上转移时间tf-t0＞0这一约束条件.

1.3 最优条件

太阳帆时间最优控制的目标函数为

构造该系统的Hamilton函数［10-11］

式中λ=［λ1λ2λ3λ4］T为协态变量.

λ2=常值(当且仅当θ(tf)为任意值,

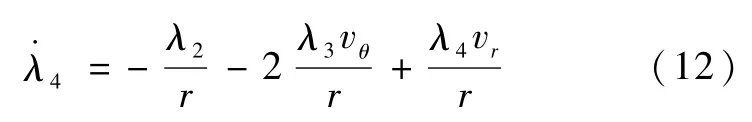
根据Pontryagin极小值原理,最优控制输入u*≡α*使Hamilton函数H最小

其中x*和λ*表示最优状态和协态矢量.即最优方向角α*可以通过∂H/∂α=0得到,即

由协态方程(9)～(12)和式(13)可以看出,最优控制输入可由协态变量初值完全确定.因此,可将协态变量初值作为寻优变量,从而太阳帆转移轨道优化问题可以转化为一个多约束多变量优化问题,寻优参数为

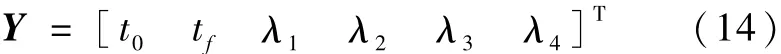
2 基于遗传算法的轨道转移算法

遗传算法是基于自然选择和基因遗传学原理的一种自适应全局优化概率搜索算法.它通过对参数空间编码并用随机选择作为工具来引导搜索过程向着更高效的方向发展［12］.为获得太阳帆转移轨道的全局最优解,需要采用遗传算法这种大范围搜索特性的全局搜索算法对上述非线性规划问题进行求解.本文针对轨道转移这一多约束优化问题,提出了基于精英解保持遗传算法的轨道转移算法.

2.1 编码方式

编码的目的是为实现交叉、变异等类似生物界的遗传操作.编码方式有许多种,与求解速度、计算精度有直接关系,对算法有重要影响.针对自变量定义域范围不大和个数不多的特点,可以采用二进制编码.这种编码方式可在保证求解精度的情况下,使编码、解码、交叉、变异等遗传操作更容易实现.

2.2 交叉算子(C rossover Operator)

交叉算子是对两个相互配对的染色体按某种方式相互交换其部分基因,从而形成两个新的个体,以实现高效搜索的重要算子.利用交叉有可能将父代个体在子代组合成具有更高适应度的个体,这是遗传算法区别于其他传统优化方法的主要特点之一.

2.3 变异算子(M utation Operator)

变异算子是以很小的概率随机地改变一个基因位的值.如对于二进制串来说,即是将随机选取的串位由1变为0或由0变为1.变异的概率通常是很小的,一般只有千分之几.遗传算法的变异特性可以使求解过程随机的搜索到解可能存在的整个空间,因此可以在一定程度上求得全局最优解.

2.4 选择算子(Selection Operator)

选择算子设计为精英解保持的轮盘赌选择算子.父代种群中各个个体被选入到子代种群的概率与其适应度大小成正比.每个个体被选择的概率可以用下面公式表示:

式中 fi表示第i个个体的适应度,n表示种群中的个体数.最优秀的若干个体(一般取一个或两个)被作为精英解直接选入到子代种群中.这实际上是对“自然选择,适者生存”的模拟.

2.5 算法框架

基于上述问题编码和遗传算子设计,提出的算法框架如图2所示［13-15］.

图2 算法框架Fig.2 Main steps of algorithm

3 基于动态罚函数的约束处理方法

种群经交叉算子和变异算子作用后,产生的新个体必然包含不可行解,所以必须要进行约束处理.目前对于遗传算法优化处理约束问题的研究成果较多,罚函数是最重要而常用的约束处理方式之一.罚函数设计难点在于惩罚系数的取值.如果惩罚系数取值过小,惩罚机制失效,导致遗传算法收敛速度变慢,且种群中不可行解数量增加；如果惩罚系数取值过大,会造成过度惩罚,导致演化过程提早收敛.在演化过程起始阶段,要求惩罚系数较小,使得算法能在解空间中更大范围内搜索问题的最优解.在演化结束阶段,则要求加大惩罚力度,保证种群中的个体尽可能地满足约束条件.定义转移轨道的罚函数为［16］

当满足约束条件时,S=0,无论M多大,则F≡J,即不受惩罚.当不满足约束条件时,S＞0,并且约束条件被破坏得越厉害,S＞0取值也就越大,从而F=J+MS也就越大,即对于约束条件被破坏是一种惩罚.惩罚因子M越大,惩罚得越厉害,根据经验计算可以选取Mi+1=cMi,取c∈［10,1000］.

对于与火星交会的转移时间tf-t0＞0这一约束条件,可以将式(14)中第二个优化参数 tf换成另一个优化参数td,表示飞行所用时间,只要让其大于零即可.此方法还允许预估飞行时间的上限,以减少算法搜索时间.

4 试验与分析

针对从地球同步轨道出发到火星同步轨道转移和从地球出发与火星交会转移,采用以上给出的基于遗传算法的轨道转移算法,进行数值仿真.地球和火星的轨道半径分别为r0=1AU、rf=1.524AU (1AU=1.49597870×1011m,表示太阳到地球的距离).选取太阳帆特征加速度ac=0.5mm/s,寻优参数为式(14),对于算例4.1由于与发射具体日期无关,故可以减少一个优化变量t0.协态变量初值的上下界虽然可以取正负无穷,但实际计算的时候一般合理地给定,算例中取 ±5之间.经过反复调试,在算法的运行时间和收敛性上做了平衡,遗传算法的参数最终设定为种群代数 Gmax=100,种群大小为40,交叉概率为0.8,精英解保持个数为2.

4.1 火星同步轨道转移

对于同步轨道转移模型,图3给出了太阳帆从地球同步轨道到火星同步轨道的转移轨迹,图4给出了最终求得的火星轨道转移过程中太阳帆方向角的变化过程.仿真后得到的其飞行时间是558.18d,协态变量初值 λ0=［-1.609601 0.042179 -0.160488 -1.597537］T.

4.2 与火星交会转移

对于与火星交会轨道转移模型,图5给出了太阳帆从地球出发飞到火星的转移轨迹,图6给出了最终求得的飞往火星过程中太阳帆方向角的变化过程.由于该模型比同步轨道转移模型多一个约束θ(tf)=θf,因此相应增大了算法搜索时间.假定任务要求的发射时间段为2011年1月1日到2013年1月1日,任务允许的最大转移时间为800d.仿真后得到的其飞行时间是575.51d,协态变量初值 λ0=［-1.899293 -1.602220 2.492184-2.030905］T.文献［6］给出的太阳帆地火转移轨道飞行时间是620d,该算法得到的结果则比此文献给出的结果要少44.5d.

4.3 分析结果

为了说明算法的有效性和控制律的可行性,表1给出了算法得到的结果与设计值之间的相对误差.无论是间接法还是直接法都是无法完全满足最优轨道的约束条件,因为总会产生相对误差.从表1的数据可以看出,该算法得出的相对位置和速度误差是在允许的范围内.之所以算例4.2飞行所需时间比算例4.1多,是因为算例4.2多一个相位约束θ(tf)=θf,那么太阳帆需要更多的时间来调整相位.给出的两组协态变量初值都非常没有规律,要在收敛半径很小的解空间内猜测这样的初值是非常困难的.因此,该套算法可以为非轨道专家的研究者提供一个合适的解决方案.

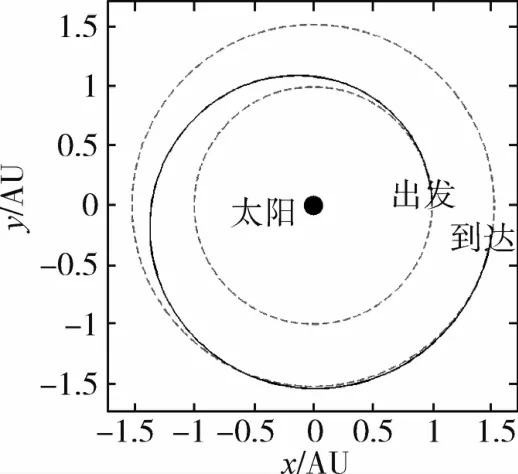
图3 地球-火星同步轨道转移轨迹Fig.3 Earth-Mars synchronous orbit transfer trajectory

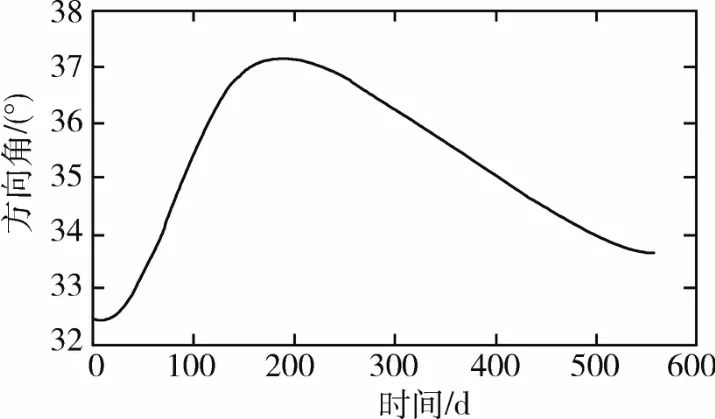
图4 地球-火星同步轨道的太阳帆方向角变化Fig.4 Time history of sail direction angle for Earth-Mars synchronous orbit

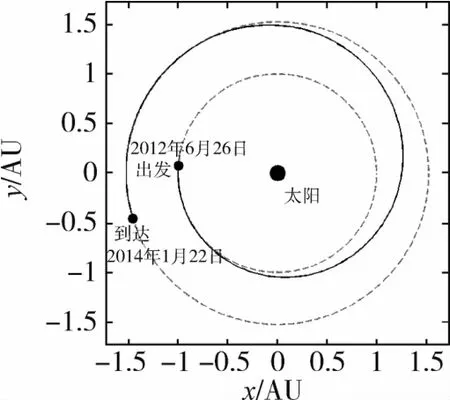
图5 太阳帆与火星交会转移轨迹Fig.5 Transfer trajectory of solar sail rendezvous with Mars

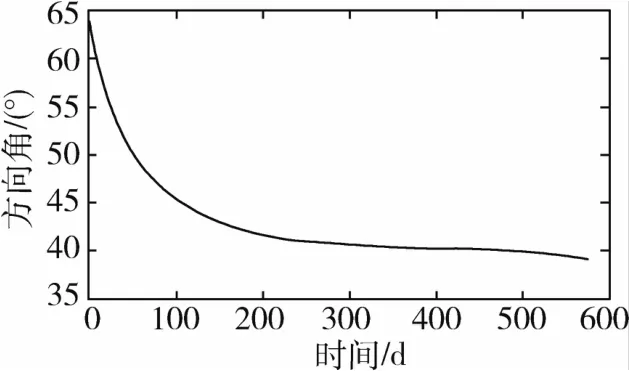
图6 太阳帆与火星交会转移的方向角变化Fig.6 Time history of sail direction angle for rendezvousing with Mars

表1 相对误差Tab.1 Relative errors

从上面两个算例的方向角变化图可以看出,方向角变化比较平缓,没有任何尖刺或者突变,这对控制系统的要求就不太高,并且太阳帆属于大型挠性结构,这样简单平滑的控制律也比较容易在太阳帆工程上实现.

从上面两个算例的轨迹图可以看出,如果不需要与火星交会的话,太阳帆能够以双曲超越速度快速将有效载荷送往火星同步轨道.交会任务的整个飞行轨迹分为两个阶段:第一个阶段是太阳帆以外螺旋轨迹飞往火星轨道；第二阶段是太阳帆进行调相,此时太阳帆飞行弧段处于火星轨道之外不远处调整相位和速度,最终到达火星.

5 结 论

本文研究了基于遗传算法的太阳帆行星际转移轨道的全局优化问题.将太阳帆转移轨道优化问题转化为一个多约束多变量优化问题,从而可以使用带罚函数的遗传算法对这个非线性规划问题进行求解.数值结果表明,基于遗传算法的轨道转移算法可以有效解决行星际太阳帆转移轨道优化问题.尽管该套算法在解空间中搜索非常高效,但由于遗传算法并没有使用任何梯度信息(这是遗传算法的特征),它并不能保证快速收敛到全局最优解附近,因此并不能保证准确得到全局最优解,有可能得到的是次优解.同时,在太阳帆轨道运动的优化中,考虑姿态运动和挠性振动的影响以及遗传算法的收敛性能、搜索效率和自适应性是应进一步深入研究的方向.

［1］ Mori O,Tsuda Y,Sawada H,et al.World’s first demonstration of solar power sailing by IKAROS［R］.The 2ndInternational Symposium on Solar Sailing,New York,USA,July 20-22,2010

［2］ 罗超,郑建华,高东.太阳帆航天器的轨道动力学和轨道控制研究［J］.宇航学报,2009,30(6):2111-2117 Luo C,Zheng JH,Gao D.Study on orbit dynamics and control of solar-sail spacecraft［J］.Journal of Astronautics,2009,30(6):2111-2117

［3］ Gong S P,Gao Y F,Li JF.Solar sail time-optimal interp lanetary transfer trajectory design［J］.Research in Astron.Astrophys,2011,11(8):981-996

［4］ 贾灵伟,张洋,王永.基于粒子群算法的太阳帆同步轨道轨迹优化 ［J］.电子技术,2010(7):11-14 Jia LW,Zhang Y,Wang Y.Trajectory optimization of solar sail for synchronous orbit base on particle swarm optimization algorithm［J］.Electronics R&D,2010(7):11-14

［5］ Dachwald B,Seboldt W.Optimization of interplanetary rendezvous trajectories for solar sailcraft using a neurocontroller［C］.AIAA/AAS Astrodynamics Specialist Conference and Exhibit,San Francisco,USA,2002

［6］ McInnes C R.Solar sailing:technology,dynamics,and m ission applications［M］.London:Springer Verlag, 1999,112-151

［7］ Kim M.Continuous low-thrust trajectory optimization: techniques and applications［D］.Virginia Polytechnic institute and State University,2005

［8］ 王松霞,徐世杰,陈统.太阳帆飞行器轨道动力学分析 ［J］.中国空间科学技术,2006,26(2):30-37 Wang S X,Xu S J,Chen T.Orbit dynamics analysis of solar spacecraft［J］.Chinese Space Science and Technology,2006,26(2):30-37

［9］ W ie B.Thrust vector control of solar sail spacecraft［C］.AIAA Guidance,Navigation,and Control Conference and Exhibit,San Francisco,USA,2005［10］ Kim M,Hall C D.Symmetries in the optimal control of solar sail spacecraft［J］.Celestial Mechanics and Dynamical Astronomy,2005,92:273-293

［11］ 胡寿松.自动控制原理 ［M］.5版.北京:科学出版社,2007,543-584 Hu S S.Theory of autocontrol［M〛.Beijing:Science Publishing Company,2005,543-584

［12］ 孙增圻.智能控制理论与技术 ［M］.北京:清华大学出版社,1997,345-372 Sun Z Q.Inetlligent control theory and technology［M］. Beijing:Tsinghua University Press,1997,345-372

［13］ 陈浩,李军,唐宇,等.基于动态罚函数遗传算法的电磁探测卫星多星规划方法 ［J］.国防科技大学学报,2009,31(2):44-50 Chen H,Li J,Tang Y,et al.An approach for electromagnetic detection satellites scheduling based on genetic algorithm with dynamic punish function［J］.Journal of National University of Defense Technology,2009,31(2):44-50

［14］ 尚海滨,崔平远,乔栋.基于微分进化的行星际小推力轨道全局优化方法 ［J］.北京理工大学学报, 2010,30(11):1275-1280 Shang H B,Cui P Y,Qiao D.Global optimization of interplanetary low-thrust trajectory based on differential evolution［J］.Transactions of Beijing Institute of Technology,2010,30(11):1275-1280

［15］ 汤一华,陈士橹,徐敏,等.基于遗传算法的有限推力轨道拦截优化研究 ［J］.西北工业大学学报, 2005,23(5):671-675 Tang Y H,Chen S L,Xu M,et al.A genetic algorithm (GA)method of orbit interception with finite thrust［J］. Journal of Northwestern Polytechnical University,2005, 23(5):671-675

［16］ 唐焕文,秦学志.实用最优化算法［M］.大连:大连理工大学出版社,2004,344-350 Tang H W,Qin X Z.Practical methods of optimization［M］.Dalian:Dalian University of Technology Press, 2004,344-350

［17］ Zhang M R,Wang G L,Sun Y.Solar sail trajectory optim ization for Earth-Marsmission［C］.The 29thChinese Control Conference,Beijing,China,2010

Op tim ization A lgorithm for Interp lanetary Transfer Trajectories of Solar-Sail Spacecraft

QIAN Hang1,2,ZHENG Jianhua1
(1.Center for Space Science and Applied Research,Chinese Academy of Sciences,Beijing 100190,China；2.Graduate University of Chinese Academy of Sciences,Beijing 100190,China)

Minimum-time orbit transfers for solar sail spacecraft base on genetic algorithm(GA)are explored.The optimal control law is derived from the maximum principle,minimum time consumption is chosen as the optim ization objective,and the launch date,the arrive date and the initial guess of the costates are optimized by using GA.In order to dealwith the design of transfer orbitwith many constraints, the penalty function is introduced into the GA.Orbit transfers for solar sail from Earth’s synchronous heliocentric orbit to Mars’synchronous heliocentric orbit and from Earth to Mars have been designed and simulated as examples.Results of simulation show correctness and practicability of proposed orbit transfer algorithm.

solar sail；global optim ization；genetic algorithm(GA)；transfer orbit；penalty function

V249

A

1674-1579(2012)01-0018-05

钱 航(1987-),男,硕士研究生,研究方向为太阳帆航天器轨道和姿态动力学控制与仿真；郑建华(1966-),女,研究员,研究方向为飞行器动力学、控制与仿真.

*太阳帆民用航天资助项目.

2011-10-12

DO I:10.3969/j.issn.1674-1579.2012.01.003