考虑杆件弹性和三维间隙铰机构动力学研究
周益君,关富玲
(浙江大学建筑工程学院,310058杭州)
随着航天科技的快速发展,对可展机构的动力学性能要求越来越高.机构展开过程中,由于间隙的非线性影响,常会出现伸展机构失稳、定位精度不够、天线打开失灵等情况,导致航天器失效.如Hubble望远镜由于间隙引起太阳能帆板冲击和振动[1].同时随着部件尺寸增大,结构重量减轻,刚度减弱,构件的弹性影响不容忽视,1958年美国发射的第一颗人造卫星“EXPLORER-I”,由于在动力学建模时没有计及4根鞭状天线的弹性影响,导致卫星入轨后翻滚、失控[2].针对可展机构中常见的旋转铰节点间隙,Dubowsky等[3-5]进行了长期的理论和实验研究,提出目前常用的非线性弹簧阻尼模型;占甫等[6]考虑了三维铰节点中轴向和径向间隙的影响,但没有考虑杆件的弹性效应;陈滨等[7]只考虑结构中的一个平面间隙铰和一根柔性杆件的影响;阎绍泽等[8-9]对含间隙铰结构进行了动力学实验,但只是测量了结构展开终了后的动力学特性,没有在展开过程中测试,同时缺乏与理论分析的对比.
为了更准确考察机构在太空中的展开动力学特性,本文从实际的三维间隙铰节点出发,同时考虑杆件弹性效应,建立动力学模型,对可展机构的展开过程进行仿真分析.为了使仿真分析更加可靠,将理论和实验两者结合.设计了一个动力学实验,通过加速度响应反映含间隙铰和杆件弹性对构件展开过程的非线性影响[9-12],实验加速度值与数值仿真进行对比,来初步验证仿真分析中动态特性的正确性.
1 含三维间隙铰动力学模型
1.1 铰间间隙描述
理想的旋转铰没有间隙,销轴和轴套只存在绕公共轴线的相对转动.如图1所示的二维平面铰,销轴与轴套之间存在沿销轴径向的间隙.而实际的铰节点是三维的,同时存在轴向和径向间隙[6],见图2.轴套沿轴向在左右挡块之间可以晃动,当轴套与销轴挡块发生该方向碰撞时,称之为轴向碰撞(图3(a));同时轴套沿径向也能晃动,当轴套与销轴发生该方向碰撞时,称之为径向碰撞(图3(b));而且轴向和径向碰撞还可能同时发生(图3(c)).
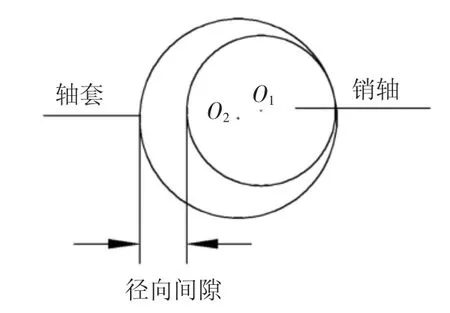
图1 只考虑径向间隙的平面铰节点
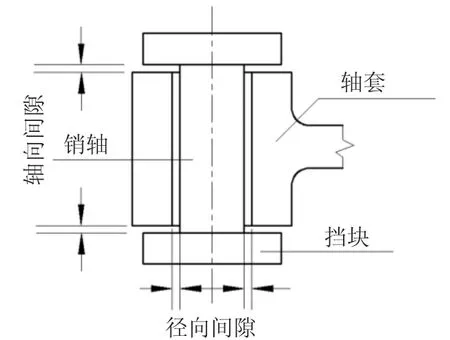
图2 三维间隙铰节点

图3 碰撞形式
1.2 铰接触力模型
间隙铰在运动过程中分为“自由运动”和“接触变形”两种状态,本文中采用Lankarani和Nikravesh[4-5]在赫兹接触力模型基础上提出的非线性弹簧阻尼模型,在这个模型中法向接触力FN表示为穿透深度δ和接触点法向相对速度的˙δ函数:

两接触面还存在相对滑动,选择库仑摩擦模型来模拟切向碰撞接触力Ff,即滑动摩擦力与正压力成正比,其方向与相对滑移速度方向相反.

式中:Ff为接触处滑动摩擦力,μd为动摩擦系数,ν(q,˙q,t)为接触点处的相对滑移速度.
1.3 “T”字形模型
根据文献[6],通过含间隙铰节点的销轴和轴套端点坐标可以得到最小距离及接触碰撞的穿透深度δ,为了能够表达节点的“实体”特征,通过“T”字形杆单元模型来简化模拟三维间隙铰节点,见图4.杆件13代表销轴(或轴套),杆件24是与之相连的杆件,点1与点3是销轴(或轴套)的端点.
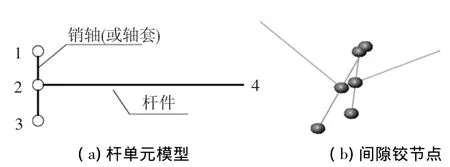
图4 “T”字型单元模型
杆12与杆23在同一直线上,同时杆12⊥杆24,杆23⊥杆24,得约束方程:
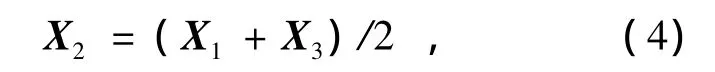

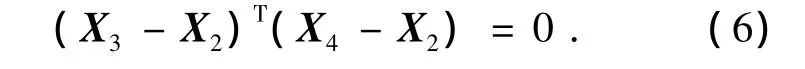
Xi= [xi,yi,zi]T(i=1,2,3,4)为点 1、2、3、4的坐标向量.
“T”字形模型保留了销轴和轴套的端部节点信息,同时增加实际运动约束相应的约束方程,通过仿真得到各时刻节点位置,从而可以求得各时刻销轴和轴套的最小距离,为判断间隙节点状态提供保证.
1.4 含三维间隙铰分离接触切换点判别
数值计算中需要对“接触”和“分离”过程的切换点进行判别.从三维间隙铰节点几何构形出发,得到销轴和轴套间在销轴轴向和径向最小距离的解析表达,构造三维间隙铰节点接触与分离的切换点判别条件[6].销轴和轴套在销轴轴向和径向的拓扑识别方程为 Si(t)=0(i=1,2),i=1和2分别表示销轴和轴套在销轴轴向和径向的拓扑结构转换识别方程.
销轴和轴套处于分离状态时:

销轴和轴套处于接触状态时:

理论上对Si(t0)=0(i=1,2)的时刻t0即为切换点,但是数值计算中无法精确找到对应的时刻t0.采用一维搜索的方法:给定足够小的时间步长Δt,当满足判别式
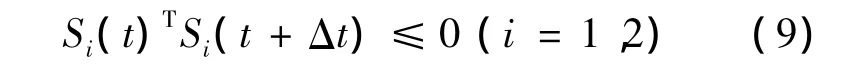
由于Δt足够小,在这区间内只有一个切换点,式(9)即为分离接触切换点判别方程.
1.5 弹性机构动力学模型
采用笛卡尔广义坐标 q=[qT1,qT2,…,qTn]T,在“自由运动”阶段,三维间隙铰节点处销轴和轴套不存在约束,此阶段动力学方程为[14-16]
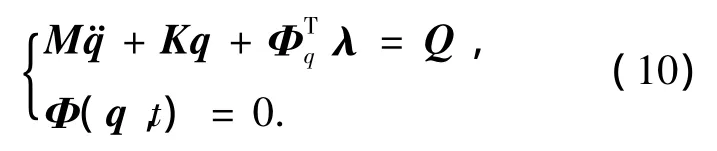
式中:M为广义质量阵,Q为广义力矩阵,Φq为约束方程的雅可比矩阵,λ为拉各朗日乘子列阵;Φ(q,t)=0为可展机构理想铰约束方程.
在“接触变形”阶段,间隙铰中销轴轴套由分离状态切换到接触变形状态,产生了约束条件的变化,解除间隙铰处的运动学约束,引入非线性弹簧阻尼模型,即以约束力代替[17],此阶段动力学方程为
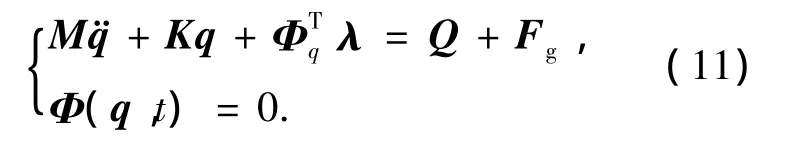
式中:Fg为接触力相对于笛卡尔广义坐标q的广义接触力.对于三维间隙铰节点,轴套与销轴间轴向接触和径向接触可能同时发生,此时对应的广义接触力Fg同时包括轴向和径向的法向接触力、切向库仑摩擦力.
2 可展动力学仿真
取某空间可展桁架的一个单元作为计算模型,固定BC杆件,其展开过程见图5.由伺服电机通过沿斜杆BD方向的驱动索提供驱动力展开到预定位置,电机转速35r/min.杆件材料为双向纤维轧制而成的碳素纤维管,杆AB、AD、BC、CD均为长度500mm,外径10mm,壁厚0.5mm,杆DE、BF长650mm,壁厚0.5mm,外径分别为9mm、10mm,杆DE和BF形成套筒可相互滑动.关节采用硬铝材料.假设节点B、C、D处为理想铰节点,A处铰节点中含铰接间隙,见图5(a)铰A详图,取销轴轴向的间隙最大值为δml=0.5mm,沿销轴径向的间隙最大值为δmr=0.5mm.当考虑杆件弹性时,杆AB、AD、BC、CD均为弹性杆件.由于可展桁架工作环境在太空,忽略重力的影响,动力学仿真所需参数见表1.

表1 动力学仿真参数
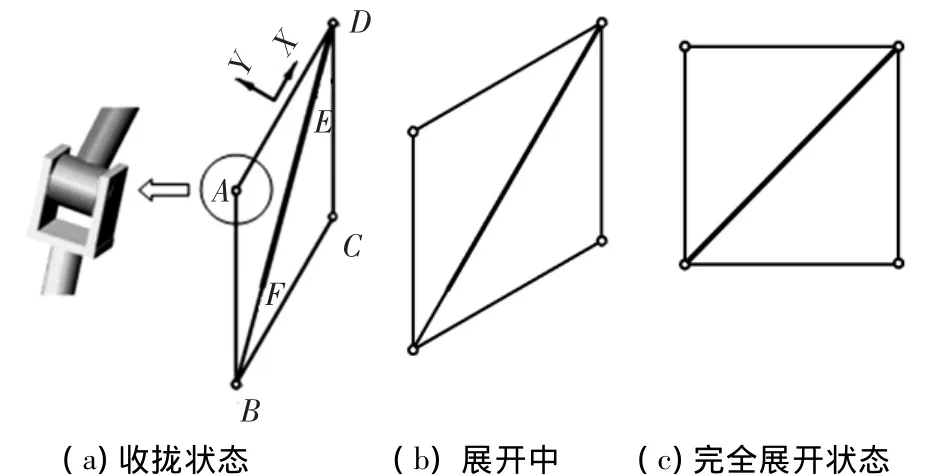
图5 含三维间隙模型的展开过程
2.1 间隙铰碰撞接触力
机构展开过程中,三维间隙铰A的径向和轴向碰撞接触力见图6、7.从图6可知,理想铰约束力很小,而间隙对展开过程产生了不可忽略的影响.无论是只考虑间隙,还是同时考虑杆件弹性和间隙,三维间隙铰的径向碰撞力在整体趋势上沿着理想铰间力上下波动.在轴套绕着销轴从静止到运动的过程中,间隙铰发生较强烈的接触碰撞,产生最大的接触碰撞力.只考虑间隙影响时,径向碰撞力达到最大25.57N,而同时考虑杆件弹性的影响,碰撞力最大为20.34N,因为杆件弹性变形消耗了部分能量,所以最大幅值有所降低.
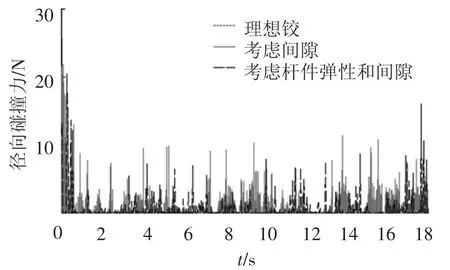
图6 铰A的径向碰撞接触力
不考虑杆件弹性效应时,每隔一段时间,径向接触碰撞力集中出现,并出现较为剧烈的波动,有一段时间又接近于理想铰约束力,如5.6~7.2s区段,11.9~13.6s区段.考虑杆件弹性影响下,径向接触碰撞力频繁出现,但数值上比只考虑间隙时小,这是弹性杆件引起间隙铰内高频振动所致.
理想铰中没有轴向约束碰撞力,但对于三维间隙铰模型,轴套和销轴挡块之间还存在轴向间隙,当轴套在挡块间左右运动时,产生正负轴向碰撞力.从图7可知,轴向碰撞没有径向碰撞频繁,在整个展开过程中,只考虑间隙时发生两处碰撞,而考虑杆件弹性和间隙时,发生6处碰撞,但碰撞接触力都较小.由于杆件弹性振动,使得间隙铰更容易发生轴向碰撞.虽然轴向力相对于径向力小,但桁架平面外刚度比平面内刚度要小得多,偶尔较小的轴向接触力对桁架产生振动,影响机构展开的精度和稳定性.所以有必要考虑弹性机构在轴向上引起的碰撞.

图7 铰A的轴向碰撞接触力
2.2 杆件弹性和间隙对机构运动过程的影响
理想铰,只考虑间隙,同时考虑杆件弹性和间隙这3种模型下的杆件AD质心的加速度和速度曲线分别见图8、9.与图6所示的径向碰撞力相对应,轴向间隙产生的碰撞次数少,碰撞力数值小,对加速度和速度的影响相对径向间隙要小.杆件弹性和间隙对运动过程产生较大的振动,数值上围绕理想铰的加速度和速度上下波动.从图9可知,考虑杆件弹性效应,构件在整个过程中波动更加频繁,由于能量的消耗,幅值比只考虑间隙时小.
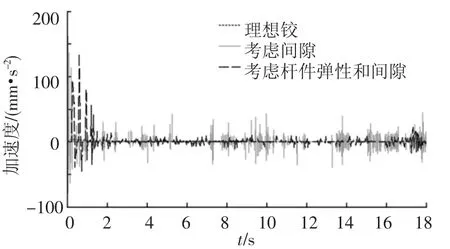
图8 杆件AD质心的加速度曲线
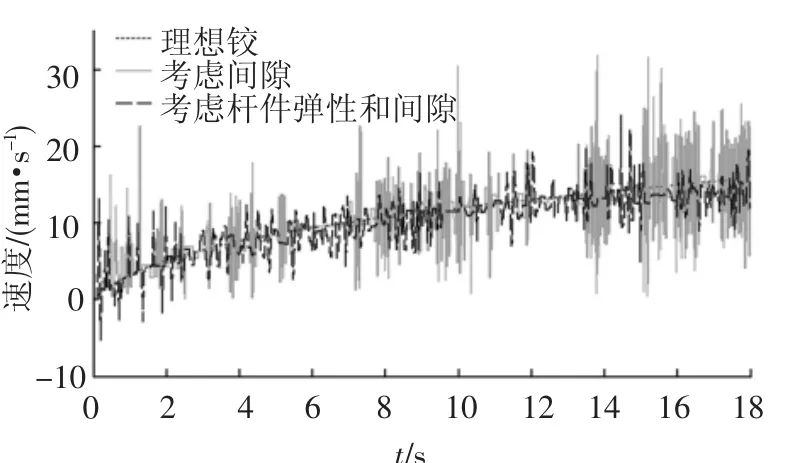
图9 杆件AD质心的速度曲线
图10所示为销轴和轴套中心在径向的相对运动.未发生碰撞时,销轴和轴套的中心点相互重合,运动后销轴和轴套接触,两中心点的相互运动限制在以0.25mm为半径的圆形区域内,并有穿透现象,即超出圆弧的部分.由于构件展开到指定位置所经过的角度较小,没有超过90°,发生单边碰撞,在这个过程中,运动集中在1/4圆内.可以看出,不考虑杆件弹性时,接触区域小而集中,而考虑杆件的弹性效应后,由于杆件弹性振动对间隙铰轴套和销轴相对位置产生影响,接触区域明显扩大.
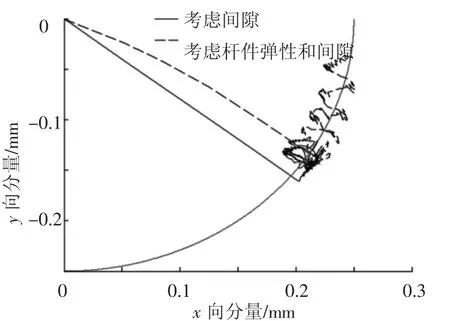
图10 销轴和轴套中心在径向的相对运动
图11所示为销轴和轴套中心在轴向的相对运动.销轴和轴套两中心点的相互运动限制在±0.25mm的带状区域内.在带状范围内时,轴套与挡块是分离的,没有轴向接触力,运动到边界时发生碰撞,有穿透现象,与图7所示发生轴向碰撞接触力的时刻相对应.考虑杆件弹性时,两中心点的相对运动路径比只考虑间隙时要复杂,说明杆件弹性引起间隙铰销轴和轴套的轴向振动.
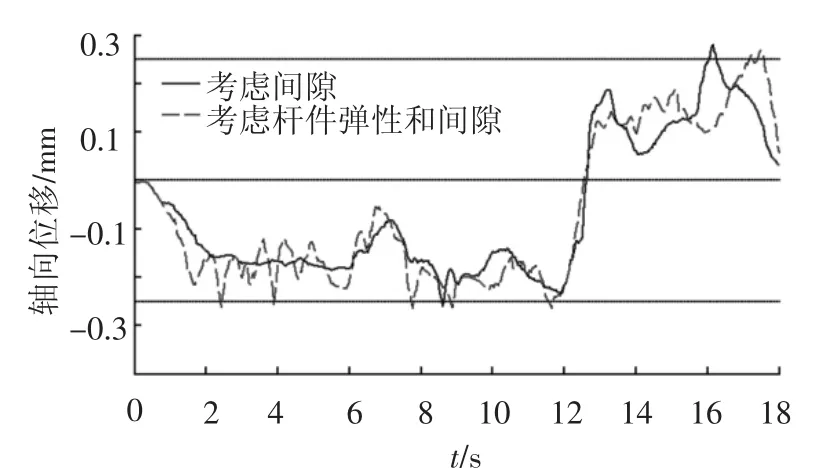
图11 销轴和轴套中心在轴向的相对运动
3 实验研究
3.1 实验系统
制作了一个单元桁架进行实验研究,杆件和节点材料与仿真相同.制作过程中,杆件两端镶嵌铝制左右旋螺纹接头,与转动铰关节相连,其特点是杆长长度可调,便于安装.转动副关节采用硬铝材料.如图5铰A中存在间隙,其他旋转铰运动副中引入组合轴承尽可能消除其间隙的影响.其转动关节主要由U形接头、销轴、组合轴承和柄舌组成,见图12.组合轴承外圈与柄舌孔之间、销轴与U形接头的安装孔之间、销轴与组合轴承的内圈之间均为过盈配合.其中,组合轴承加工时,在轴承与轴承毂的配合面上涂敷一层液体胶膜,保证两者的紧密接触,消除可能出现的空行程[18].通过这些措施来达到理想铰的效果.为了模拟太空环境,尽可能消除重力影响,使单元水平安装,每根杆件都用弹性绳悬挂,水平放置时见图13.

图12 无间隙转动关节组成
实验中使用CA-YD-117型压电式加速度传感器,YE5858A型电荷放大器,CRAS振动及动态信号采集分析系统.由12V微型直流电机提供驱动力,转速35 r/min.测展开过程中杆件AD质心在Y向的加速度响应.实验原理见图14.

图13 实验模型

图14 实验原理图
3.2 实验结果
图15为实验测得的杆件AD质心Y向加速度曲线,图16为依照前述的理论仿真,同时考虑间隙铰和杆件弹性得到的杆件AD质心Y向加速度曲线.两者在运动趋势上能较好吻合,说明理论分析基本的正确性.但在实际模型中,加工精度不可能做到完全理想的状态,这也会影响展开过程中的非线性响应.同时,实验过程中传感器的重量和精度等外在条件也使结果有一定的误差.所以图15中的加速度曲线波动较图16所示的理论分析要剧烈.
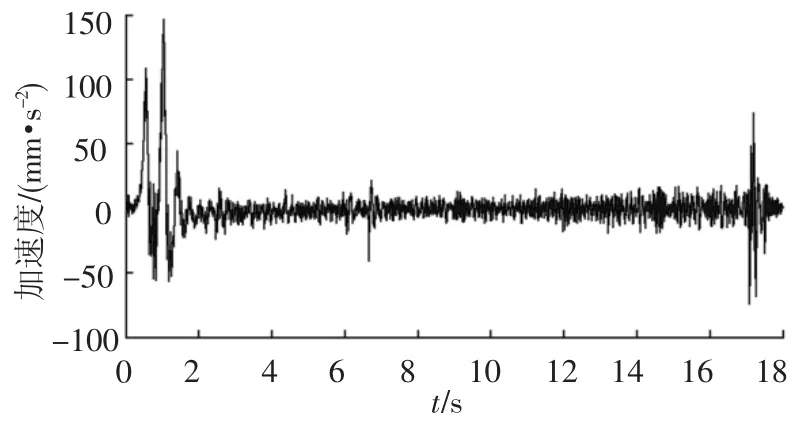
图15 实验中杆件AD质心Y向加速度曲线
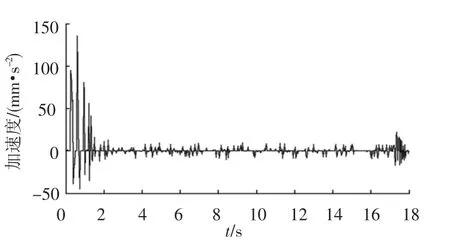
图16 数值仿真杆件AD质心Y向加速度曲线
4 结语
通过建立考虑杆件弹性和三维间隙铰动力学模型,对可展机构进行展开数值模拟.分析表明,运动副间隙和构件的弹性对机构动态响应的影响很大,如简单地按理想机构进行计算,必将引入较大的误差.碰撞接触力在考虑杆件弹性时要小于只考虑间隙因素,由于杆件弹性振动效应,使轴套和销轴的碰撞更加频繁,轴向碰撞对桁架面外产生波动,影响可展机构的展开过程的稳定性.对精密的机构进行动力学分析时,引入实际的间隙铰模型和考虑杆件弹性效应是必要的.设计了动力学实验,通过引入组合轴承来模拟理想铰的效果,可展桁架的动力学实验结果反映出间隙和杆件弹性带来非线性的动力学响应,与理论结果趋势相吻合.目前国内从理论和实验两方面同时研究尚且缺乏,亟待进一步深入.
[1]NURRE G S,SHARKEY J P,NELSON J D,et al.Preserving mission,on-orbit modifications to hubble space telescope pointing control system [J].Journal of Guidance,Control,and Dynamics,1995,18(2):223 -230.
[2]陆佑方.柔性多体系统动力学[M].北京:高等教育出版社,1996:6-35.
[3]DUBOWSKY S,FREUDENSTEIN F.Dynamic analysis of mechanical systems with clearances[J].Journal of Engineering for Industry,1971,93(1):305 -316.
[4]LANKARANI H M,NIKRAVESH P E.A contact force model with hysteresis damping for impact analysis of multibody systems[J].Journal of Mechanical Design,1990,112:369 -376.
[5]LANKARANI H M,NIKRAVESH P E.Continuous contact force models for impact analysis in multibody systems[J].Nonlinear Dynamics,1994,5:193 -207.
[6]占甫,关富玲.含三维间隙铰空间可展机构动力学数值分析[J].浙江大学学报:工学版,2009,43(1):177-182.
[7]陈滨,潘寒萌.含铰接间隙与杆件柔性的空间伸展机构单元的动力学建模与计算模拟(第一部分:动力学建模)[J].导弹与航天运载技术,1997,1:27-37.
[8]阎绍泽,陈鹿民,吴德隆,等.空间可展结构非线性动力学特性实验研究[J].宇航学报,2002,23(4):1-4.
[9]陈鹿民,阎绍泽,金德闻,等.含间隙铰空间可展桁架结构的动力学实验[J].清华大学学报:自然科学版,2003,43(8):1027 -1030.
[10]李哲,张渊.含间隙机构混沌响应的实验研究[J].北京工业大学学报,1994,20(4):34 -38.
[11]TASORA A,PRATI E,SILVESTRI M.Experimental investigation of clearance effects in a revolute joint[C]//Proceedings of 2004 AIMETA International Tribology Conference.Rome:Firenze University,2004:352-360.
[12]TASORA A,PRATI E,SILVESTRI M.A compliant measuring system for revolute joints with clearance[C]//AITC -AIT 2006 International Conference on Tribology.Parma:Parma University,2006:726 -732.
[13]HUNT K H,CROSSLEY F E.Coefficient of restitution interpreted as damping in vibroimpact[J].Journal of Applied Mechanics,1975,42:440-445.
[14]阎绍泽,申永胜,陈洪彬.考虑杆件柔性和铰间隙的可展结构动力学数值模拟[J].清华大学学报:自然科学版,2003,43(2):145 -148.
[15]FLORES P,AMBROSIO J.Revolute joints with clearance in multibody systems[J].Computers and Structures,2004,82:1359 -1369.
[16]FLORES P.Modeling and simulation of wear in revolute clearance joints in multibody systems[J].Mechanism and Machine Theory,2009,44:1211 -1222.
[17]SCHWAB A L,MEIJAARD J P,MEIJERS P.A comparison of revolute joint clearance models in the dynamic analysis of rigid and elastic mechanical systems[J].Mechanism and Machine Theory,2002,37:895-913.
[18]于登云,杨建中.航天器机构技术[M].北京:中国科学技术出版社,2011:27-54.

