松花江流域水环境化学耗氧量模拟及参数分析

李 平，马 放

(哈尔滨工业大学城市水资源与水环境国家重点实验室，150090哈尔滨)

污染物进入河流，在河流水动力的作用下发生稀释、扩散、沉降、降解，这一过程的模拟和预测，需要根据河流水文特点、污染物的性质建立相应水质响应模型，来描述水体中污染物随时间和空间迁移转化规律［1－3］.水质模拟过程是利用水体历史数据、污染物的物理化学演变规律，建立相应的数学、物理、化学及实验模型，进而描述水体中污染物质与河流水质之间的响应关系，对河流水环境系统进行模拟、预测和评价，水质模拟是水环境监督管理的重要工具［4-12］.水质模型研究是从1925年 H.Streeter和E.Phelps提出的BOD和DO之间耦合关系一维数学方程开始，1970年，EPA开始推出QUAL水质综合模型，先后开发出了QUAL－Ⅱ、QUAL2E、QUAL2E－UNCAS、QUAL2K 等一维平移－弥散质量迁移水质模型［13］.1983年，US EPA 又开发了应用于河流、水库、河口、海岸水质分析模拟的通用WASP模型体系，可进行一维、二维、三维水质模拟［14］.1993年，丹麦开发了 MIKE模型体系，包括多用于模拟一维河流水体的一维动态模型MIKE11、多用于具有垂向变化湖库的二维动态模型 MIKE21 和三维空间模型 MIKE3［15-17］.水质模型规格化、模块化，集成化程度不断加深拓展，但水质模拟参数的研究是准确分析仿真的前提和必要基础，是进一步降低水质模型失真度、提高水质模型预报精度的必要工作.

本研究利用水团追踪及罗丹明B示踪实验获得的数据，重点探讨了佳木斯江段河流水质扩散特性，研究了佳木斯江段平水期和冰封期的COD模型，识别了相应特征参数，验证了模型的有效性，确定了松花江佳木斯段横向、纵向扩散系数，为进一步精确可靠的流域水质模拟研究提供参考.

1 实验

1.1 水质模型建立基本方法

建立水质模型应首先根据研究对象的建模目的、研究范围、河流特点，分析河段水质模拟需求和水质的时空分布规律，按照模拟需求进行数据收集和资料整理工作.结合河流水质的特点，确定COD指标作为控制因子，结合河流水文水质特点，确定相应水质模型描述污染物输入和水质输出的关系.模型建立后，利用相关水文和实验数据进行计算机求解模型，确定水质模型参数后对模拟的可靠性进行检验.

1.2 水团追踪及罗丹明B示踪实验

淡水、河水、海水中的弥散仅从理论上分析较困难，采用现场示踪试验，选用易溶于水、稀溶液呈强荧光的工业染料碱性罗丹明B为示踪剂，采用荧光分光光度法进行测定，确定纵向弥散系数，研究干流扩散规律.示踪剂罗丹明B(分析纯)瞬时投放，在河流的下游布置断面采样，样品送回化验室检测，波长578 nm定量，水质指标采用国家标准方法［15］测定.

利用人工投放的方式在河道中造成一个含有机物的污水团进行水团跟踪监测，利用污水团沿程浓度衰变情况推定河流对污染物质的降解规律.BOD20为现场测定，枯水期、平水期在佳木斯江段前后两次共进行水团追踪作业，1月水温为0℃，各断面采样时间为佳木斯下1:00，桦川6:00，新城14:30，富锦18:00.6月水温为14℃，各断面采样时间为佳木斯下8:00，桦川19:00，新城8:00，富锦4:00.

2 结果与分析

2.1 河流水质扩散研究

天然河流的宽深比一般较大，污染物在垂向一般比较均匀，可用二维扩散模型分析其扩散过程.若河道均匀平直，横向流速可以忽略，并认为纵向流速和纵、横方向的扩散系数皆为常数，则扩散模型基本方程为

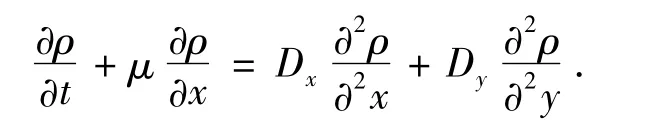
在无限宽边界中瞬时点源条件下的解析解为

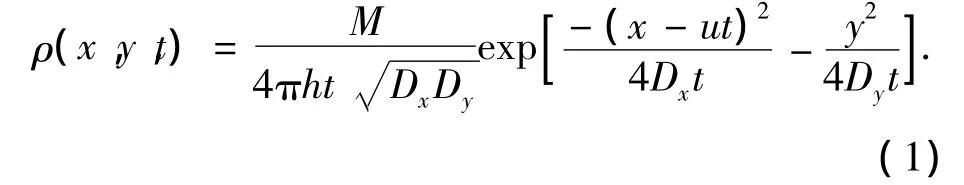
其中:x、y为纵、横距离(m);ρ为垂向平均质量浓度(mg/m3);μ为流速(m/s);Dx、Dy为纵、横向扩散系数;t为时间;h为水深(m).

2.1.1 扩散系数估值

河流扩散系数取决于河流深度和摩擦速度，摩擦系数又与河深、河面坡度有关，另外河流宽度和河道河曲弯度对河流横向扩散有影响.扩散系数可由下面公式求出:

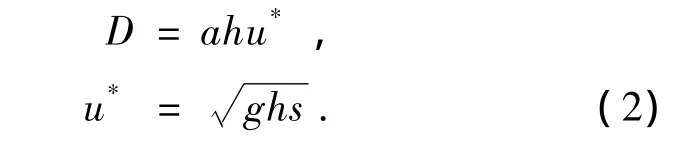
式中:D为河流扩散系数(m2/s);h为河深(m);u*为摩擦速度(m/s);g为重力加速度(m/s2);s为河面坡降;a为经验常数，求横向、纵向扩散系数时，其经验常数分别为0.23和5.96.

研究江段中深度变化较小，最深处约为5 m，浅处为2 m，平均水深为3.36 m.整个研究江段河底较为平坦，江宽平均为800～1 200 m，江段底质为砂砾，江面坡度为0.015%.

1)信号重叠是植物提取物中复杂光谱的一个问题，妨碍了提取物的识别和量化，因此需要更好的信号分辨率。多维核磁共振波谱法的共振信号分别在多个独立的频率轴上传播，从而减少了信号重叠，但多维核磁共振波谱法的局限是采集时间较长。近年来报道了一种称作Hadamard谱的快速多维谱方法[49]，在相同的分辨率和信噪比的前提下，基于Hadamard的信号采集时间比传统方法减少约20倍，因此Hadamard谱或许会成为新的研究趋势。

根据式(2)求出整个研究河段摩擦速度平均值u*=0.070 3(m/s)，粗略估算研究江段的横向扩散系数为 0.054 m2/s，纵向扩散系数为1.41 m2/s.由于估算未计入河宽、河曲以及流速变化的影响，一般较试验求得数值要小1～2个数量级.

2.1.2 试验江段水文特征

松花江佳木斯江段全长201 km，流经佳木斯、桦川、绥滨、富锦、同江等市县，并与黑龙江汇合于同江市.松花江下游地处三江平原，河道宽，分叉较多.历史上径流量年变化幅度较大，存在明显的丰、枯周期.枯水年与丰水年径流量比为1∶1～6(佳木斯断面).试验江段为松花江下游佳木斯－富锦江段，江段长167 km，河道弯曲系数为1.17.

根据26年水文资料统计，研究江段多年平均流量为2 150 m3/s，多年最大流量为18 400 m3/s是多年最小流量的100余倍，表明该江段流量变化很大.在染料释放期间，即6月份流量为3 840 m3/s，研究江段平均流速为1.05 m/s.通过平水期在松花江佳木斯江段染料(罗丹明B)示踪试验，采用瞬时点源形式释放，以人工一次性倾倒式投药，距离排放点(高程76.2 m)约4 km处设监测断面(高程75.6 m)，对其浓度进行判断，以多元回归方法求出扩散基本方程解析式，进而确定相应扩散系数.

2.1.3 扩散特征研究

染料自释放点向下游纵向迁移的同时亦进行横向扩散.据资料报道，染料混合后，不论横向或纵向扩散，开始为偏态分布，以后接近正态分布.由图1可以看出，位于接近河流中泓线的点染料质量浓度分布也基本趋于正态，染料在断面横向的质量浓度分布基本接近正态(图2).

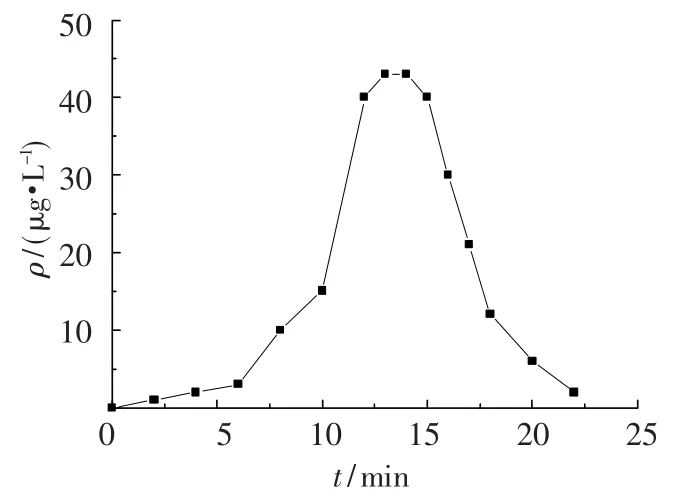
图1 河流中泓线断面质量浓度分布

图2 横断面质量浓度分布

示踪试验数据显示，示踪剂质量浓度分布基本呈正态分布，以扩散方程解析式来推求扩散系数.将式(1)两端同乘以t，然后分别取对数，可变化成下列形式:

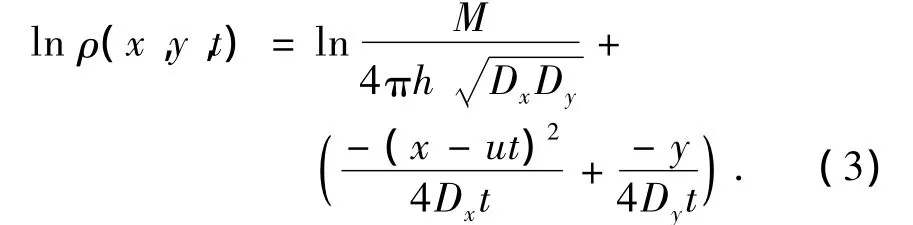
2.1.4 扩散系数计算结果

研究江段的扩散系数按染料实验求得，表1列出松花江佳木斯江段扩散系数计算结果.最终确定松花江佳木斯江段横向扩散系数为0.41m2/s，纵向扩散系数为43.51m2/s，为进一步精确可靠的流域水质模拟研究奠定基础.因横向扩散系数较纵向扩散系数小两个数量级，影响较小，本文只考虑水体纵向扩散作用.

表1 松花江佳木斯江段扩散系数 m2·s-1

2.2 化学耗氧量模型

2.2.1 模型的选择

河流水质模拟计算中，综合衰减系数起着非常重要的作用［18］.通过对松花江水系部分江段COD监测，发现COD在最初阶段质量浓度下降较快，但随着水团流动距离的增加，COD质量浓度下降速度逐渐减缓，最终趋于稳定.质量浓度负荷变化规律符合负指数方程，选用一级反应速率方程来表征河段COD水质变化特征.

微分方程形式为

此微分方程解为

式(4)和(5)为稳态条件下基本模型，并未考虑河流弥散作用［19］.综合河流的稳态弥散作用，以对松花江佳木斯江段进行更精确的模拟，将式(4)右侧增加相应的弥散作用表达式，即

式中:L为水质质量浓度(mg·L-1);L0为初始COD质量浓度(mg·L-1);t为流程时间(s);K1为综合衰减速率(d-1);D为扩散系数(m2/s)，初值条件L(x=0)=L0.

2.2.2 模型参数

1)参数识别方法.流速与纵向弥散系数是反映河流特征的重要参数，河流纵向弥散系数与流速之间的关系可以采用以下公式表达

式中:u*为摩擦速度(m/s);u为平均速度(m/s);b为水面宽(m);h为水深(m).

表2列出了佳木斯江段1月及6月两次化学耗氧量测试结果.共计8组实测数据，5组用于参数识别，3组用于参数验证.其中1、2号数据用于冰封期参数识别;5～7号数据用于平水期参数识别，3、4、8号数据用于参数验证.

2)参数识别结果.将表3的冰封枯水期(水温0℃)1～4号数据和平水期(水温14℃)8～10号水团追踪数据输入式(7)，识别流速和扩散系数结果见表4.

表2 松花江佳木斯段COD实测结果

表3 模型参数识别输入

表4 参数结果

将表4结果和冰封枯水期(水温0℃)1～2号数据和平水期(水温14℃)水团追踪数据输入，利用已知的x(距离)、质量浓度L以及初始质量浓度L0、弥散系数D、平均流速u，拟合式(6)计算识别化学耗氧量水质模型参数K1，冰封期和平水期K1，结果见表5.

表5 参数识别结果

利用模型参数修正方程基本型式K(T)=K(20)·θT-20，对计算所得衰减系数进行温度修正.式中θ为温度修正系数，K(T)为任意温度(T)下的参数;K(20)为20℃ 下的参数.根据表5的参数识别结果进行温度修正，得到水温20℃ 下衰减系数K为0.188 d，温度系数θ为1.109 8，任意温度下衰减系数经验式为

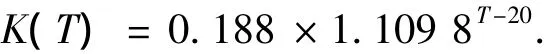
3)参数验证结果.由表4结果可知，冰封期流速不足平水期流速1/2，冰封期扩散系数更远较平水期扩散系数小，水温直接导致冰封期COD衰减系数远小于平水期COD衰减系数.分别利用冰封期3、4号和平水期8号数据进行参数验证，相应参数输入见表6，验证结果如表7所示.

冰封期流速0.41m/s、扩散系数6.65m2/s、平水期流速1.05m/s、扩散系数43.51m2/s条件下，通过模型输入计算，最小相对误差0.31%，最大相对误差8.55%，实测COD和模拟值的相对误差控制在10%以内，满足《水污染物排放许可证技术报告编写指南》对模型误差应控制在±40%精度要求［20］.所获取的水质模型参数值模拟精度较高，应用在松花江佳木斯段水质模拟中较合适.文中所获得的扩散系数和降解系数将为进一步提高河段水质模拟精度和COD总量控制提供数据和理论支撑.

表6 模型参数验证输入

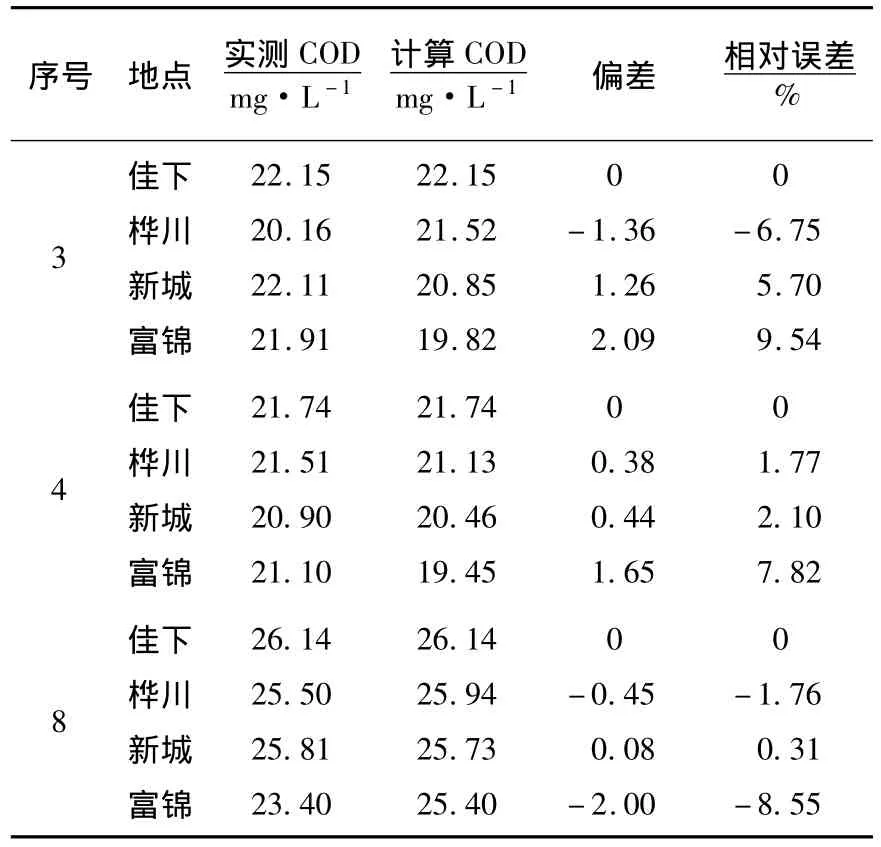
表7 松花江化学耗氧量模型验证结果

3 结论

1)通过罗丹明B示踪实验分析，确定了松花江佳木斯段横向扩散系数为0.41 m2/s，纵向扩散系数为43.51 m2/s，比估算值高一个数量级，为进一步精确可靠的流域水质模拟研究奠定基础.

2)确定了松花江佳木斯段COD衰减系数K(20)=0.187，计算模拟结果和实测COD相对误差都在10%以内，表明该模型应用在松花江佳木斯段水质模拟中较合适.

3)对松花江佳木斯段COD模型参数进行了温度参数修正，得到任意温度下衰减系数经验式K(T)=0.188 ×1.109 8T-20.

［1］李兰.水质多参数辨识与反演算法［J］.水利学报，1998(6):46－52.

［2］MACAVOY D C，MASSCHELEYN P，PENG C，et al.Risk assessment approach for untreated wastewater using the QUAL2E water quality model［J］.Chemosphere，2003，52:55－66.

［3］郭德伟，韩光明，田秀丽，等.复杂边界河流水质预测计算［J］.山东农业大学学报，2008，39(4):553－556.

［4］刘伟，刘洪超，徐海岩.基于MIKE11模型计算河流水功能区纳污能力方法［J］.东北水利水电，2009，8:69－72.

［5］金春久，王超，范晓娜，等.松花江干流水质模型在流域水资源保护管理中的应用［J］.水利学报，2010，41(1):86－92.

［6］LEE J H W，JAYAWARDENA A W，WANG Z Y.Proceeding of international conference on environmental hydraulics［M］.Northland:A A Balkman，1999:387 －392.

［7］张波，王桥，李顺，等.基于系统动力学模型的松花江水污染事故水质模拟［J］.中国环境科学，2007，27(6):811－815.

［8］张荔，王晓昌.水文水质综合模型与城市小流域河流污染分析［J］.西安建筑科技大学学报，2007，39(4):569－574.

［9］PORTER A L，FITTIPALDI J J.Environmental methods review:retooling impact assessment for the new century［M］.Fargo，North Dakota，USA:The Press Club，1998:100-106.

［10］MARSILI-LIBELLI S，GIUSTIA E.Water quality modelling for smallriver basins［J］.Environmental Modeling＆ Software，2008，23(4):451－463.

［11］MARTINEZ C J，WISE W R.Analysis of constructed treatment wetland hydraulics with the transient storage model OTIS［J］.Ecological Engineering，2003，20:211 －222.

［12］付彩菊.河流水污染定量研究进展［J］.环境科学与管理，2007，32(9):59－61.

［13］曹永中，周孝德，吴秋平，等.河流水质模型研究概述［J］.水利科技与经济，2008，14(3):197 －200.

［14］TORO di D M，SIFITZPATRICK J J.Documentation for water quality analysis simulation program(WASP)and model verification program(MVP)［M］.Duluth，MN:US Environmental Protection Agency，1983.

［15］Danish Hydraulics Institute.MIKE11:user guide and reference manual［R］.Horsholm，Denmark:［s.n.］，1993.

［16］Danish Hydraulics Institute.MIKE21:user guide and reference manual［R］.Horsholm，Denmark:［s.n.］，1996.

［17］Danish Hydraulics Institute.MIKE3:eutrophication module，user guide and reference manual［R］.Horsholm，Denmark:［s.n.］，1996.

［18］马常仁，徐得潜，周慧，等.基于最小二乘法与最速下降法的综合衰减系数的率定［J］.水利科技与经济，2012，18(1):20 －24.

［19］张解放，史忠科.河流水质分析的状态方法［J］.重庆环境科学，2002，24(2):40 －42.

［20］操群，柳炳祥，林洋.BOD－DO耦合模型在鄱阳湖入湖河流水质预测中的应用［J］.科技资讯，2011，7:132-133.