Hermite插值在一重积分Wiener空间下的平均误差

刘 洋，许贵桥

Hermite插值在一重积分Wiener空间下的平均误差

刘 洋，许贵桥

（天津师范大学数学科学学院，天津300387）

在加权L2范数下讨论基于第一类Chebyshev多项式零点的Hermite插值多项式在一重积分Wiener空间下的平均误差，得到了相应量的弱渐近阶．

Hermite插值多项式；Chebyshev多项式；一重积分Wiener空间

设F是一个实可分的Banach空间，μ是定义在F的Borel子集上的概率测度．设H为另一个范数为‖·‖的线性赋范空间，F连续嵌入到H．任意使得f→‖f－A（f）‖为可测映照的算子A：F→H被称为一个逼近算子．算子A的平均误差定义为

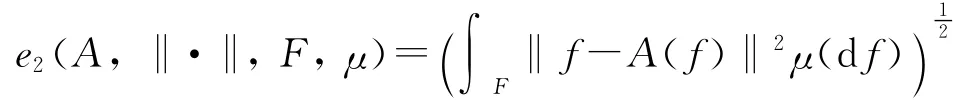
记F0＝｛f∈C［0，1］：f（0）＝0｝．对任意f∈F0，令‖f‖C＝｜f（t）｜，则（F0，‖·‖C）成为一个可分的Banach空间，用B（F0）表示（F0，‖·‖C）上的Borel类，用ω0表示B（F0）上的Wiener测度［1］．令（T1g）（t）＝∫t0g（u）du，则对任意g∈F0，

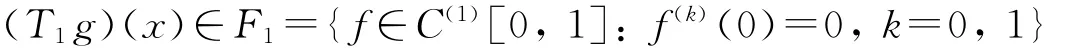
易知T1为F0到F1的一个双射．F1上的一重积分Wiener测度ω1由诱导测度ω1＝T1ω0给出，即AF1，

设F＝｛f∈C（1）［－1，1］：f（k）（－1）＝0，k＝0，1｝．F上的一重积分Wiener测度ω为：对任意AF，

对f∈C［－1，1］，定义f的加权L2范数为k＝1，2，…，n为n次第一类Chebyshev多项式Tn（x）＝cos nθ，x＝cosθ的全部零点．对f∈C［－1，1］，f的基于｛xk｝nk＝1的Lagrange插值多项式为［2］

其中：

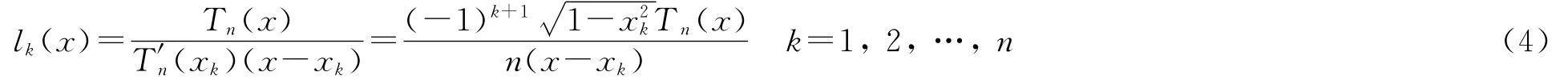
相应的Hermite－Fejér插值多项式为［3］

其中：

由文献［4］可知

对于正数序列｛an｝和｛bn｝，an≈bn表示存在与n无关的常数C，使得an／C≤bn≤Can，不同表达式中的C可能不同．由式（7）和式（8）可知，由式（3）和式（5）定义的Lagrange插值与Hermite－Fejér插值在一重积分Wiener空间下的平均误差有不同的收敛阶．由文献［5］可知，由式（3）和式（5）定义的Lagrange插值与Hermite－Fejér插值在Wiener空间下的平均误差有相同的收敛阶．这说明不同的插值算子在不同概率空间下的平均误差是需要单独考虑的．下面考虑基于｛xk｝nk＝1的Hermite插值多项式．

若f∈C（1）［－1，1］，则f的基于｛xk｝nk＝1的Hermite插值多项式Gn（f，x）为满足条件

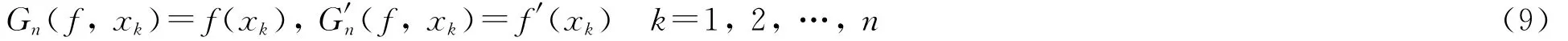
且次数不高于2n－1的代数多项式，其表达式为［6］

其中：

由文献［6］可知，若pn（x）为次数不超过2n－1的代数多项式，则有

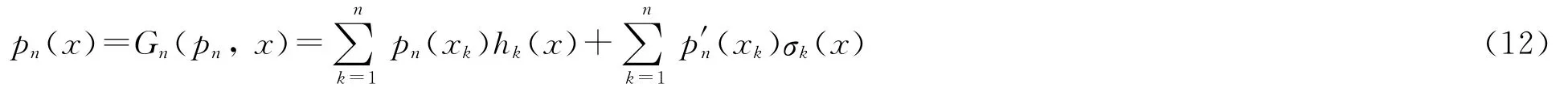
本研究得到

定理 设Gn（f，x）如式（10）定义，则

引理1［6］设σk（x）由式（11）定义，则

引理2［4］设s≥t，则有

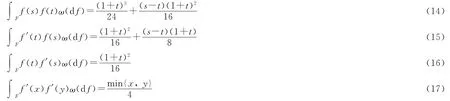
引理3 若pn（x）为次数不超过n－1的代数多项式，则

由式（18）可得，若pn（x）为次数不超过n－1的代数多项式，则

定理的证明 由文献［1］可得下估计．下面考虑上估计．由式（4）计算可得

且当j≠k时，有

由式（9）、式（20）、式（21）和式（12）可得

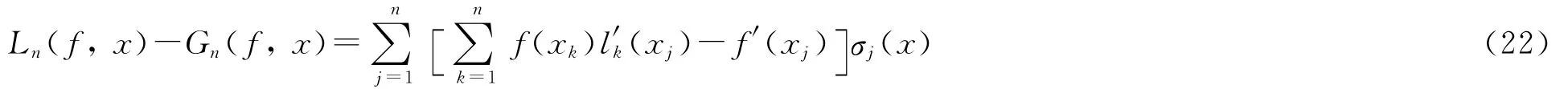
因此

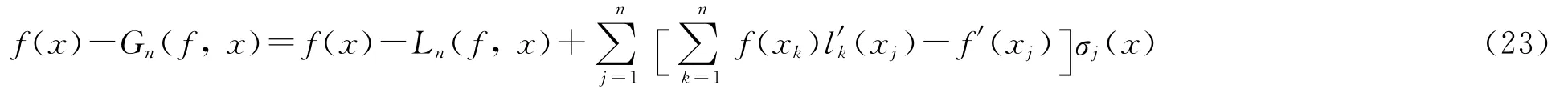
易检验

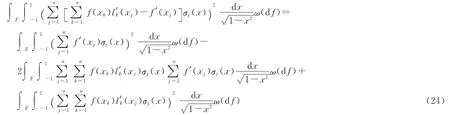
由式（13）和式（17）直接计算得

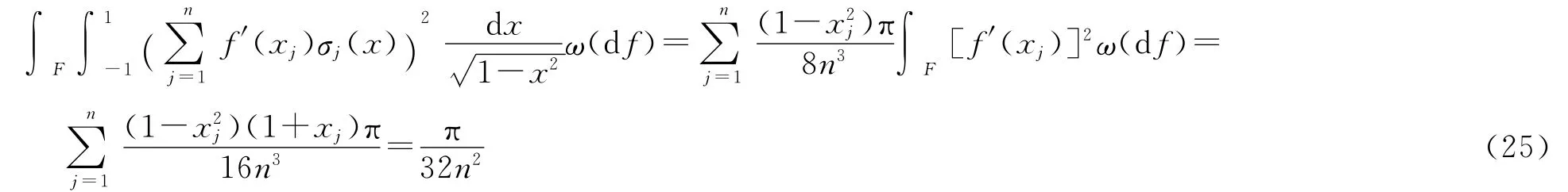
由式（13）可知

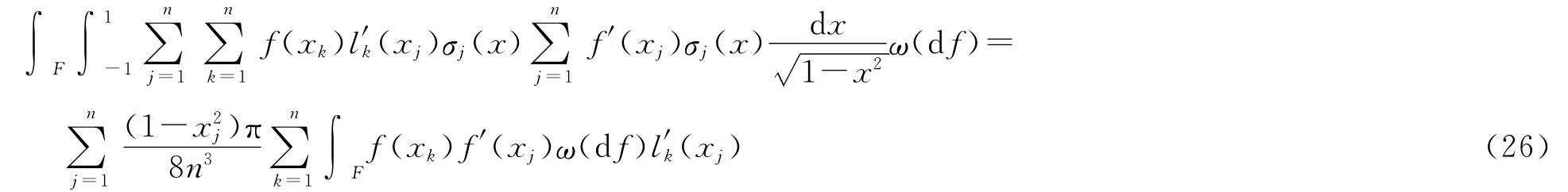
对任意1≤j≤n，由式（15）、式（16）及式（19）可得

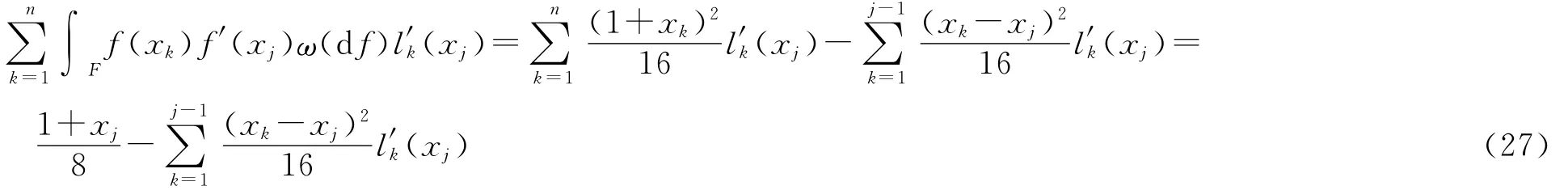
由式（26）和式（27）及文献［4］可得

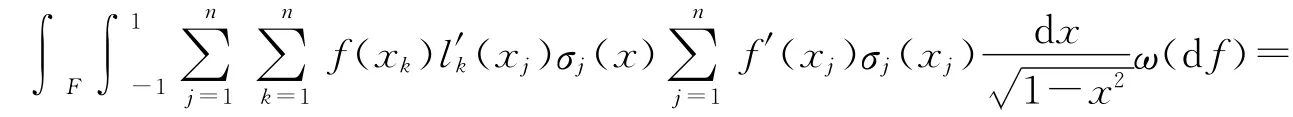
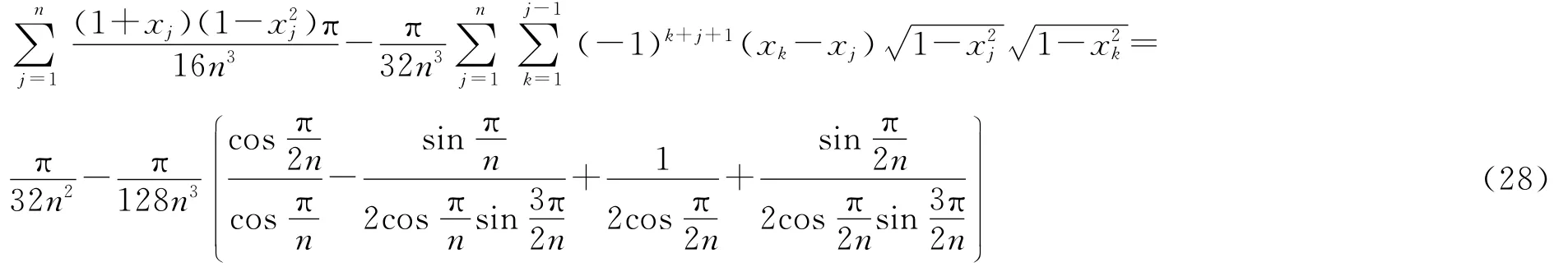
由文献［4］中定理3的证明过程可知

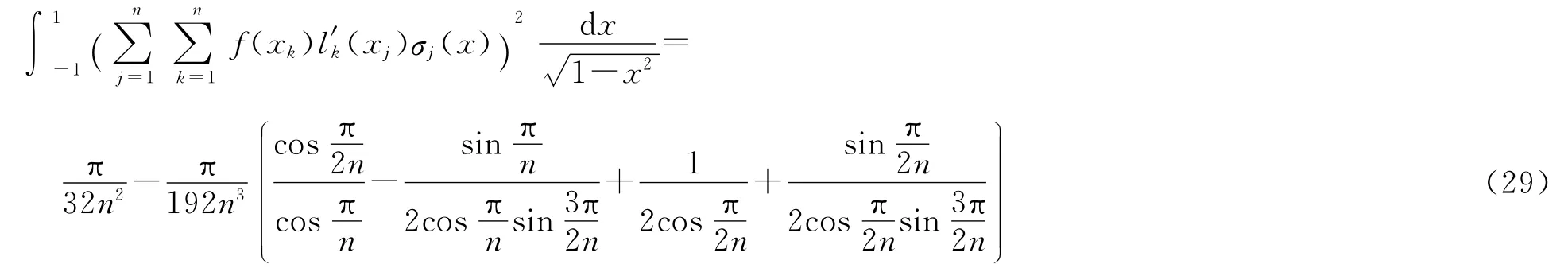
由式（24）、式（25）、式（28）和式（29）可得

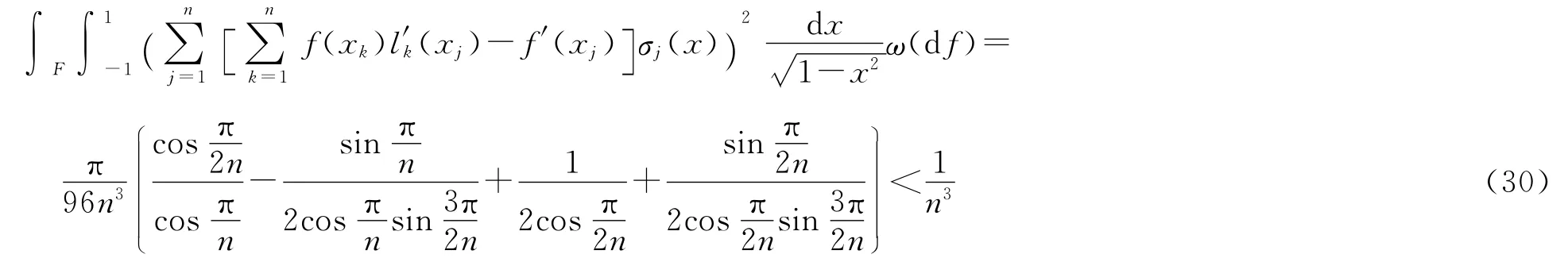
由式（23）、式（7）和式（30）可得上估计．定理证毕．

［1］ KLAUS R．Average－Case Analysis of Numerical Problems［M］．Berlin：Springer－Verlag，2000．

［2］ ERDOS P，FELDHEIM E．Sur le mode de convergence pour 1’interpolation de Lagrange［J］．C R Acad Sci Paris Ser I Math，1936，203：913－915．

［3］ FEJER L．Lagrangesche interpolation und zugehorigen konjugierten punket［J］．Math Ann，1932，106：1－55．

［4］ 许贵桥．插值多项式在一重积分Wiener空间下的同时逼近平均误差［J］．中国科学：数学，2011，41（5）：407－426．

［5］ 许贵桥．Lagrange插值和Hermite－Fejér插值在Wiener空间下的平均误差［J］．数学学报，2007，50（6）：1281－1296．

［6］ VARMA A K，PRASAD J．An analogue of a problem of P．Eros and E．Feldheim on convergence of interpolatory processes［J］．J Approx Theory，1989，56：225－240．

（责任编校 马新光）

Average error of Hermite interpolation on 1－fold integrated Wiener space

LIU Yang，XU Gui－qiao
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

In the weighted L2－norm，the average error of Hermite interpolation sequence based on the zeros of Chebyshev polynomials of the first kind on the 1－fold integrated Wiener space is discussed．The weakly asymptotically order is determined．

Hermite interpolation polynomials；Chebyshev polynomials；1－fold integrated Wiener space．

book=1,ebook=38

O174．42

A

1671－1114（2012）02－0022－04

2011－05－17

天津师范大学教学改革基金资助项目

刘 洋（1989－），女，硕士研究生．

许贵桥（1963－），男，教授，主要从事函数逼近论方面的研究．