结构分离和参数分离的灰箱建模

曹柳林，刘华，王晶，吴海燕

(北京化工大学 信息科学与技术学院，北京 100029)

建立准确的非线性系统模型是实施基于模型的先进控制策略的基础.当前，融合机理建模［1］和黑箱建模［2-3］技术的灰箱建模方法得到越来越多的研究，已显示出很大优越性.James S等［4］对一个间歇反应器进行灰箱建模，引入了神经网络对反应的反应物浓度进行了模拟.Chang Jyh-Shyong等［5］模拟间歇反应过程，使用神经网络估计反应中难以测量的状态变量.Cao Liulin等［6-7］人使用串联、并联神经网络和结构逼近式混合神经网络等方法对非线性CSTR过程建模进行深入研究.

工业生产过程存在一大类这样的对象，如CSTR，它们被广泛使用，其运行的机理框架(表现为模型的结构)基本明晰，而模型参数因品种各异而未知［8］.传统的黑箱建模方法无视这类极其宝贵的先验知识资源，仅从输入输出数据中去逼近系统.本文提出的建模方法是建立在深入、细致的分析系统特性的基础上，充分利用系统的先验知识，试图从结构和数据上逼近原型系统，以提高模型的精度和泛化性能.

1 连续搅拌釜式反应器过程描述

连续搅拌釜式反应器(continuous stirred tank reactor，CSTR)是化工生产过程中广泛常用的一种反应器.本文选取一类典型的CSTR作为建模背景［9］，如图1所示.

反应过程可简化为

其中，A和B是反应原料，C是反应生成物，K是反应速率常数.

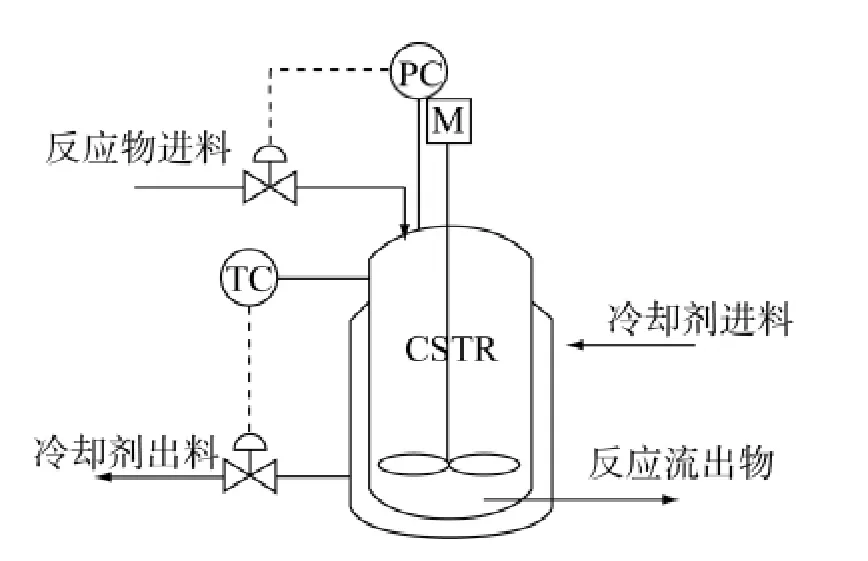
图1 CSTR反应过程Fig.1 Reaction process of CSTR

CSTR物料平衡和能量平衡方程为

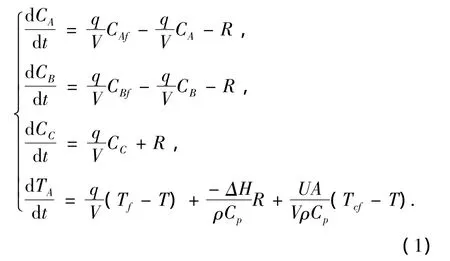
反应速率和Arrhenius方程:

式中:CA、CB是反应物A和B的浓度;CC是生成物的浓度，T是反应温度;CAf、CBf是反应物A和B的进料浓度;Tf是进料温度;Tcf是冷却剂温度;q为总进料流量;R'是气体常数.过程参数的含义及数值见表1.

根据式(1)和(2)，在对工艺分析的基础上，选择CAf、CBf、Tf、Tcf作为模型的输入变量(操纵变量和扰动变量)，CA、CB、CC、T 为状态变量(含输出变量).

在对上述对象建模中，假设其所有变量均为可测量，表1中的反应器体积也为已知量，其余参数为未知量.

方程(1)和(2)可以代表一大类典型的化学反应过程，其反应机理基本已知，但反应参数各异且未知，本文针对这类过程开展建模研究.

建模思路是充分利用系统的先验知识，最大可能的保留系统的已知结构和参数.

建模过程分两阶段进行，首先针对非线性部分，辨识出Arrhenius方程中的未知参数反应活化能E0和指前因子k0，从而计算出反应速率R;其次完成线性部分的参数辨识.这种两步法的训练模式迭代运行，直至满足模型精度的要求.

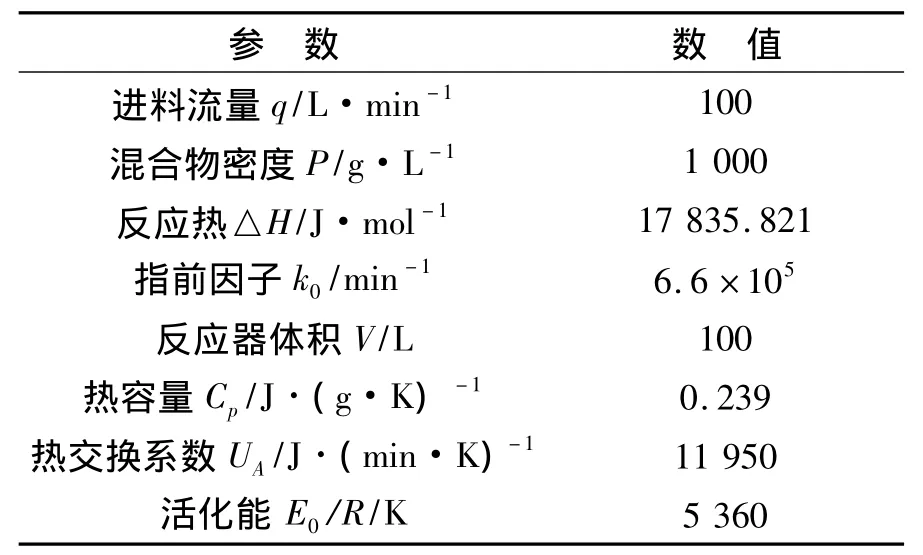
表1 CSTR参数表Table1 CSTR parameters

2 利用结构分解建立CSTR的灰箱模型

观察CSTR方程，可知反应速率R是方程中唯一的非线性因素.若对上述系统进行结构分解，把R选作系统的输入，那么这个非线性系统就可以转变成线性系统，可被线性状态方程描述.系统结构图和状态方程参见图2和式(3).

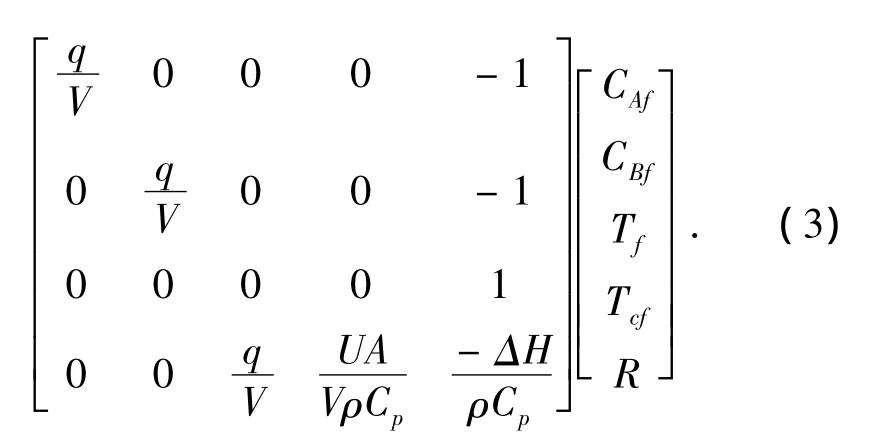
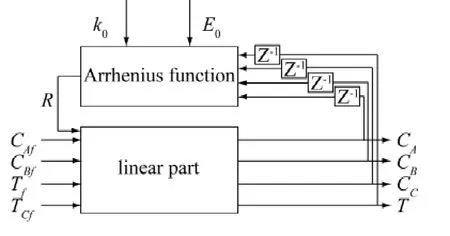
图2 模型结构Fig.2 The structure ofmodel

2.1 利用对数变换建立非线性静态部分的模型

由于由式(2)所示的反应速率及相应的Arrhenius方程已被广泛接受，提出的建模思路是尽可能保留系统的已知结构和参数，因此与常规黑箱建模方法不同，这部分模型完全继承如式(2)所示的方程形式，其中的反应活化能E0和指前因子k0需要辨识.

为使用简便、有效的最小二乘算法估计上述参数，需要对反应速率方程进行处理.

方法1 对数变换法.

两边取对数:

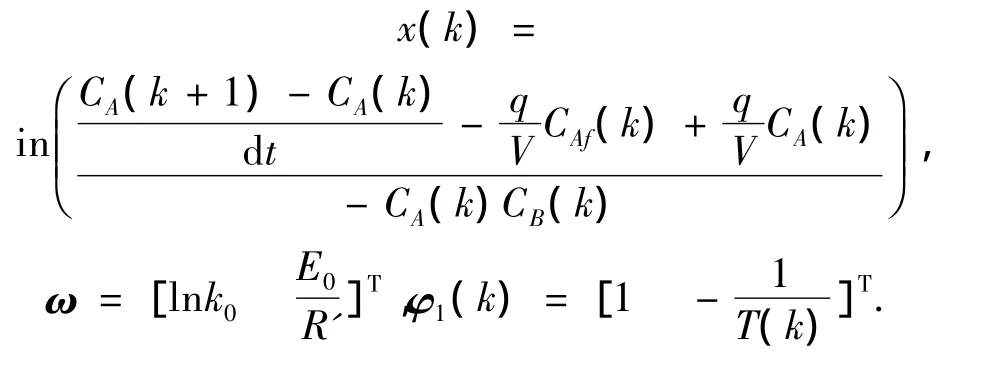
令则有

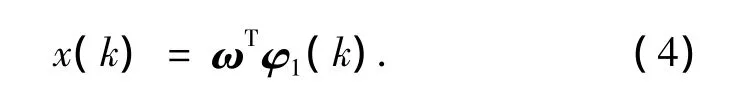
根据工艺常识的大致数量级确定E0和k0的初值，从样本集中提取适当数目的数据组成x(k)，使用递推最小二乘法将ω=［ω1ω2］辨识出来，从而求出反应活化能 E0和指前因子 k0，其中，k0=exp(ω1)，E0=R'ω2，进而获得反应速率 R.

方法2 泰勒公式法.

利用泰勒级数公式对非线性方程进行线性化，使用最小二乘法把未知参数辨识出来，从而求出反应速率，此方法在此不再赘述.

2.2 利用参数分解建立线性动态部分的模型

分析由式(3)描述的线性状态方程，可知矩阵中绝大多数元素为零或已知参数，如q.V-1和1，仅有2项元素未知.而常用的建模方法，无论是神经网络还是使用最小二乘的黑箱建模方法，均忽略了这些先验知识，对矩阵的全参数进行辨识.针对这种缺陷，本文采用参数分离的做法，固定零元素和已知量，仅对矩阵中非零的未知参数进行辨识，这样可以大大降低模型的训练时间，更重要的是可以保证从模型结构上最大可能的逼近原型系统，从而提高模型的可靠性和泛化能力.

因此

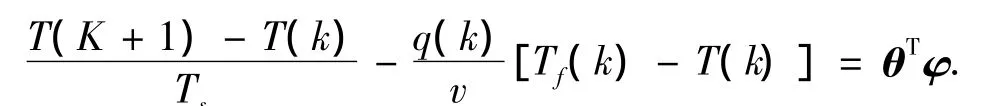
利用采集对象的样本集和递推最小二乘算法，可将θ辨识出来，再代入式(3)，确立线性部分的模型.

3 建模结果与对比

取反应物A和B的进料流量CAf，CBf以及进料温度Tf、冷却剂的温度Tcf为模型的输入信号，让其在取值域内随机变化.为模拟生产实际，在输入变量中分别加入白噪声信号，记录相应的时间响应，生成模型的训练样本集.为使模型的动态和稳态特性都满足要求，在样本集中特意增加了表现系统稳态特性的阶跃输入及其响应，它与随机信号的比例约为1∶5.

3.1 实际反应速率R与模型数值比较

为了反映所建模型与实际原型系统内部结构的逼近程度，利用机理模型R的可计算性质，与2种模型获取的反应速率做了对比，见图3．

以下比较中模型误差采用如式(5)所示的标准误差公式:

式中:n是样本总数．

由图3可以看出，方法1获得的反应速率R与实际值十分接近(标准差σ1=0．079 9)，而方法2计算出的反应速率R与实际值存在一定偏差(标准差σ2=0．171 1)．这是由于方法2使用泰勒公式近似所引起的，而方法1对Arrhenius方程做了形式上的准确变换．

3．2 2种灰箱模型与全参数辨识灰箱模型比较

为了验证提出的参数分离建模方法(仅对未知参数进行辨识)的泛化精度，与常规使用的全参数辨识的灰箱建模方法(下称方法3)进行对比(如图4所示)，同样使用反应速率R作为输入的结构分离法．

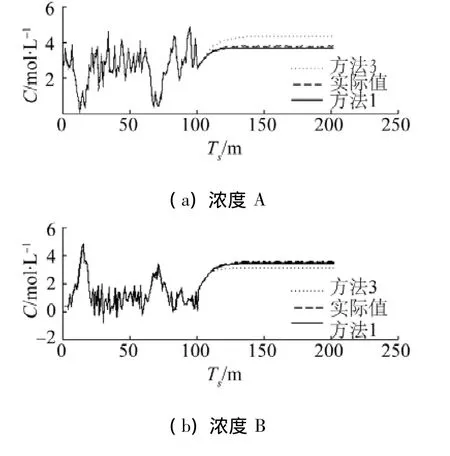
图4 方法1和方法3模型输出曲线Fig．4 Output curves of themethod 1 and method 3

由图4可知，方法1在动态和稳态特性上都明显优于全参数辨识的灰箱模型，尤其是稳态特性．在辨识浓度C和反应温度T时，方法3的动态特性也有较大的偏差．方法1充分利用系统的已知信息，不仅从外部的输入输出数据上捕捉系统的特性，更从内部结构上逼近系统的原型，因此能获得更好的模型精度．根据式(5)计算得到3种模型的标准误差见表2．

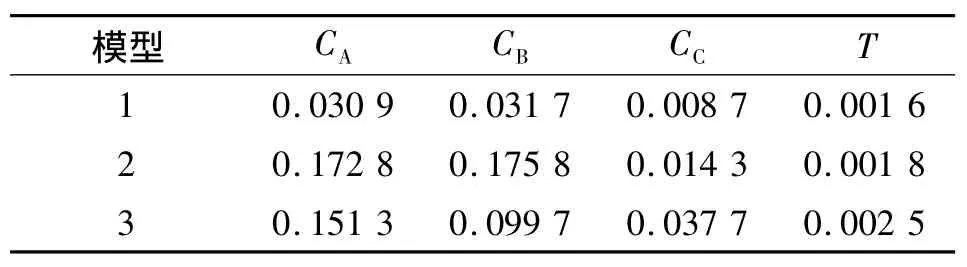
表2 3种模型的标准误差Table 2 The standard errors of the threemodels

由表2可见，方法1的各项误差都是最小的;在物料A、B的浓度误差方面，方法3要小于方法2;而物料C浓度和反应温度的误差，方法2小于方法3．方法1和方法2的误差分布比较平均，方法3则显示出较大的波动．由此可见，本文提出的灰箱建模方法需要辨识的参数大大减少，充分利用了系统的已知信息，在模型的精度和可靠性上都要好于全参数辨识的常规方法．

4 结束语

以石化工业中广泛应用的连续搅拌釜式反应器(CSTR)为背景，提出简便、有效的两步法训练的灰箱建模方法．在对CSTR机理深入分析的基础上，充分利用模型结构的先验知识，把模型描述为线性动态和非线性静态两部分，实现模型的结构分解.针对包含指数形式(Arrhenius方程)的非线性部分，提出2种数学处理方法，把其转化为线性方程，便于简捷、快速的求解;充分利用模型参数的先验知识，把线性状态方程中的已知参数固定化，仅辨识未知参数，实现模型的参数分解;通过上述两步法训练，建立起典型CSTR的灰箱模型.经与常规建模方法比较，所建模型可以提高建模的精度和可靠性，从内部结构上逼近原型系统，并大大缩短模型的训练时间.

［1］LIU Haixia，PAPANGELAKIS V G.Chemicalmodeling of high temperature aqueous processes［J］.Hydrometallurgy，2005，79(1/2):48-61.

［2］DU Jingjing，SONG Chunyue，LIPing.Modeling and control of a continuous stirred tank reactor based on a mixed logical dynamicalmodel［J］.Chinese Journal of Chemical Engineering，2007，15(4):533-538.

［3］ZHU Qunxiong，LIChengfei.Dimensionality reduction with input training neural network and its application in chemical processmodelling［J］.Chinese Journal of Chemical Engineering，2006，14(5):156-169.

［4］JAMESS，LEGGE L，BUDMAN H.Comparative study of black-box and hybrid estimation methods in fed-batch fermentation［J］.Journal of Process Control，2002，12(1):113-121.

［5］CHANG J S，LU SC，CHIU Y L.Dynamic modeling of batch polymerization reactors via the hybrid neural network rate function approach ［J］.Chemical Engineering Journal，2007，130(1):19-28.

［6］曹柳林，李晓光，王晶.利用结构逼近式混合神经网络实现间歇反应器的建模［J］.化工学报，2008，59(4):958-963.CAO Liulin，LIXiaoguang，WANG Jing.Modeling ofbatch reactor based on structure approaching hybrid neural networks approach［J］.Journal of Chemical Industry and Engineering，2008，59(4):958-963.

［7］CAO Liulin，LIDazi，ZHANG Chunyu，et al.Control and modeling of temperature distribution in a tubular polymerization process［J］.Computers ＆ Chemical Engineering，2007，31(11):1516-1524.

［8］MOHANTY S.Artificial neural network based systemidentification and model predictive control of a flotation column［J］.Journal of Process Control，2009，19(6):991-999.

［9］周东华.现代故障诊断与容错控制［M］.北京:清华大学出版社，2000:20-25.