圆柱体内线缆电磁脉冲耦合特性分析*

李春荣，王新政，吕怀武

(1.海军航空工程学院，山东烟台 264001;2.中国人民解放军93502部队，内蒙古呼和浩特 010051)

0 引言

当前强电磁脉冲武器实用化进程不断推进，电子系统面临的复杂电磁环境日益恶劣。在电子系统工作的任意瞬间，外界强电磁脉冲均可能穿透腔体上的孔缝与腔体内部的线缆耦合产生干扰电流，通过线缆回路传导进入电子系统内部造成危害。系统中各类线缆既是高效的电磁波接收天线，又是高效的辐射天线，是电磁脉冲耦合进入系统内部的重要通道［1-4］。为保证电子系统安全可靠地工作，研究强电磁脉冲对电子系统中线缆的耦合效应，对提升系统抗强电磁脉冲打击能力具有重要意义。

外部电磁能量进入腔体内部与线缆产生耦合效应分为2阶段［5-6］:一是电磁波与孔缝耦合进入腔体的过程;二是进入腔体中的电磁能量与线缆耦合产生感应电压和感应电流的过程。由于处理孔缝耦合与线缆耦合分别涉及“场”和“路”的方法，综合考虑孔缝、腔体和线缆对电磁能量耦合效应影响的研究较少，从现有研究孔缝腔体内线缆耦合问题的文献看，仅涉及了矩形腔体中无限薄的孔缝模型［7］。本文采用时域有限积分法［8-10］结合Agrawal传输线方程［11］分析了孔缝圆柱腔体中传输线的强电磁脉冲耦合效应。通过计算线缆终端差模电压的耦合系数，分析了孔缝、导线、腔体和入射电磁脉冲对线缆耦合特性的影响。

1 数学方法

根据电磁能量传递，将腔体内线缆与外界电磁脉冲的耦合过程分为2部分:一是电磁脉冲穿透腔体结构进入腔体的过程，采用时域有限积分法计算腔体内线缆位置的场分布;二是腔体中电磁场与线缆耦合产生感应电压和感应电流的过程，采用Agrawal传输线方程计算终端响应。求解过程如图1所示。

图1 弹体内线缆强电磁脉冲耦合计算流程Fig.1 Flowchart of the calculation of the termination response of cables in the cavity excited by EMP

1.1 基于时域有限积分法的场耦合模型

时域有限积分法直接离散时域Maxwell方程积分表达形式的数值方法，由Weiland T.于1976/1977提出［5-6］。该方法利用网格剖分将电场和磁场的离散在空间上错置、时间上交替，真实反映电磁波的传播。电磁问题数值分析一般包括:场域离散化和描写物理问题数学方程的离散化。其中场域离散化包括网格的划分、编号及不同介质交界面的处理;方程离散化是将连续的微分或积分方程化为用网格点上的场值表示的离散方程［7］。

1.1.1 有限积分法场域离散

有限积分法采用正交六面体对计算区域进行离散化剖分。电场矢量离散分配到G单元，称之为电场单元。离散的电场分布在相应三维网格单元G的每条边的中点处，而离散的磁场分布在相应网格单元的每个面的中点处，各个磁场方向之间构成与G相互正交的另一个立方体网格单元G～，称之为磁场单元。电场与磁场交替进行，相差半个时间步长，其形式类似于Yee氏网格单元(图2)。同样，电流密度j和各个媒质材料的介电常数ε，磁导率μ，导电率σ都可如此分配到相应的网格单元中。由此离散的电磁场在不同媒质分界面上满足连续性的边界条件。

图2 有限积分法场域离散Fig.2 Spatial discretization of Maxwell’s equations

1.1.2 有限积分法中Maxwell方程离散

有限积分离散积分形式的Maxwell方程:

有限积分理论对Maxwell方程的离散采用了一级近似，即用场的平均值与积分路径的长度Δ或面积Δ2的乘积来代替场沿线或面的积分，如图3所示。即

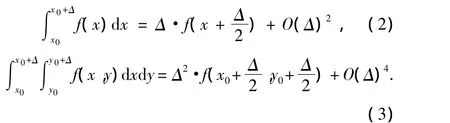
对Faraday电磁感应定律进行离散，其离散过程如图4所示。为了描述场在所有网格上离散的拓扑信息，构造由元素‘0’，‘1’和‘-1’构成的拓扑矩阵C作为旋度算子的离散等效。

同理对广义Ampère感应定律在二次网格中引入对偶离散旋度算子C～，对散度方程引入离散的散度算子S和S～，分别属于主网格和对偶网格。这些离散的矩阵算子代表了网格的拓扑信息。最后获得了完全离散化的Maxwell网格方程:

最后，材料属性由于三维离散化将不可避免地引入数值误差。在定义电压和通量的关系时，它们的整数值必须被近似在各自的网格边缘和单元面积中。网格中的材料属性依赖于平均材料参数和网格空间分辨率，其关系式为

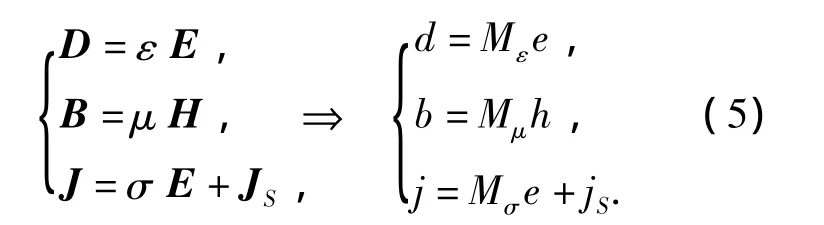
1.1.3 离散方程的求解

利用中心差分代替时间求导，产生显式迭代公式求解离散的Maxwell方程。

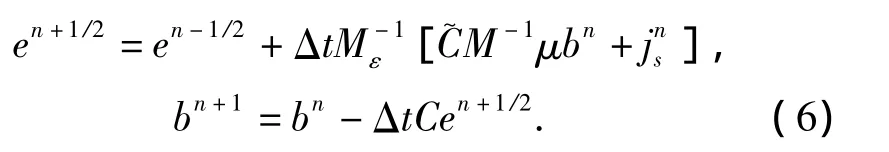
上述求解过程2种类型的未知数在时间上交替进行(如图5)。

图5 迭代求解Maxwell方程Fig.5 Iterative solution of Maxwell’s equations

1.2 基于Agrawal法的路耦合模型

采用传输线理论中Agrawal公式［11］计算双导线间的差模电压，双导体传输线模型和求解原理分别如图6、图7所示。该方法将沿导体切向入射电场看作激励传输线的分布电压源。

负载电压方程为

源矢量由入射波参数表示为

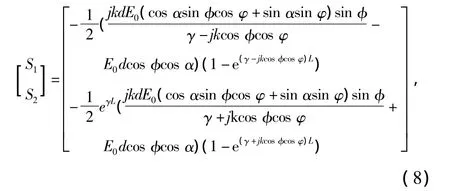
2 仿真建模

建立长为30 cm，内半径5 cm，壁厚0.2 cm圆柱腔体，腔体侧壁设置10 cm×1 cm的矩形孔，腔体材料选用理想导体;在腔体中轴敷设长20 cm，横截面积0.01 cm2的两根铜导线，导线间距0.25 cm，传输阻抗为50 Ω，导线两端接匹配负载;场强为50 kV/m高斯脉冲平面波入射，模型如图7所示。

图8 平面波激励下圆柱腔体内的线缆示意图Fig.8 Field coupling onto wires enclosed in cylindrical cavity

3 结果分析

3.1 孔缝对线缆耦合特性的影响

为研究孔缝形状对线缆耦合特性的影响，对相同横截面积(10 cm2)的矩形孔、圆形孔、椭圆形孔和正方形孔的双导线感应差模电压进行了仿真(如图8)。可见，共振效应非常明显，感应电压由高到低分别为:横向矩形孔、圆形孔、正方向孔、椭圆形孔和纵向矩形孔，横向矩形孔的感应电压远大于其他形状孔缝。分析认为，造成此现象的主要原因是导线上感应电压受孔缝和导线双重极化特性的影响，只有在孔缝、导线和入射电磁脉冲极化方向均相匹配时，感应电压才能达到最大。

图9 不同形状(相同截面积)孔缝时导线感应电压Fig.9 Induced voltage influenced by the shape of rectangular slot(with the same sectional area)

3.2 导线位置对线缆耦合特性的影响

易知腔体中场受边界条件的影响分布不均匀，为分析导线感应电压受此不均匀性的影响，在矩形孔缝10 cm×1 cm纵向轴线布线的基础上分别对横向布线、纵向布线远离孔缝和靠近孔缝3种情况的导线感应电压进行了仿真，结果如图9所示。可见，横向布线时感应电压呈指数增长，远大于纵向布线;而纵向布线时感应电压随导线和孔缝距离的增加而减小。分析认为，脉冲能量穿透孔缝耦合进入腔体中，能量集中在孔缝周围，具有共振特性和场增强效应;且孔缝和导线在耦合过程中具有明显的极化特性，极化特性可与缝隙天线和线天线类比(即:孔缝极化方向为平行于短边;导线极化方向平行于导线方向［12］)，因此横向布线时，导线、孔缝和电磁场极化特性相匹配，耦合效应显著增强。

图10 导线位置对感应电压的影响Fig.10 Induced voltage influenced by the location of wires

3.3 入射波极化对线缆耦合特性的影响

分别对线极化、圆极化和椭圆极化入射波进行仿真对比，结果如图10所示。可见，入射波极化特性改变时共振频率仅出现微小的偏移，而感应电压的大小出现显著变化，圆极化波和线极化波垂直于孔缝长边2种情形下，感应电压几乎完全重合，椭圆极化波、线极化波平行于孔缝长边时的感应电压比圆极化波大，再次说明孔缝极化特性影响耦合进入腔体中场的分布，导线极化特性影响了最终感应电压的耦合系数。

图11 入射波极化对感应电压的影响Fig.11 Induced voltage influenced by the polarization of incident wave

4 结束语

围绕圆柱腔体内线缆电磁脉冲耦合效应研究，提出了基于时域有限积分法和Agrawal传输线方程的场路耦合模型。重点研究了孔缝、线缆位置和入射波极化对线缆耦合特性的影响，得到以下看法:腔内线缆的电磁脉冲耦合特性受孔缝和线缆参数的双重影响，只有当入射波极化与孔缝、线缆极化均相匹配时，耦合系数最大;由于腔体中场分布的不均匀性，孔缝附近线缆耦合系数较大。为了更深入了解强电磁脉冲与腔体内线缆耦合的特性，还需开展腔体内多导体传输线端接有源/无源负载时耦合特性的研究。本文研究内容对提高电子系统电磁兼容性具有一定意义。

［1］ 叶红军，张武森.电子设备的射频干扰效应研究［J］.现代防御技术，2008，(3):93-97.

［2］ 谢莉，雷银照.电气系统中多导体传输线的瞬态电磁响应［J］. 电工技术学报，2010，25(5):190-194.

［3］ Yakup Bayram，John L Volakis.A Generalized Mom-Spice Iterative Technique for Field Coupling To Multiconductor Transmission Lines in Presence of Complex Structures［J］.IEEE Transactions on Electromagnetic Compatibility，2005，47(2):234-246.

［4］ WANG Jian，YIN Wen-yan，FANG Jin-peng，et al.Transient Responses of Coaxial Cables in An Electrically Large Cabin With Slots and Windows Illuminated By An Electromagnetic Pulse［J］.Progress In Electromagnetics Research，2010，106:1-16.

［5］ FISAHN S，GARBE H.Protective Properties of a Missile Enclosure against Electromagnetic Influences［J］.Advances in Radio Science，2007，(5):63-67.

［6］ 蔺安坤.车载通信总线的抗电磁干扰性分析［D］.西安:西安电子科技大学，2010:22.

［7］ YANG TAESIK，JOHN L V.Coupling Onto Wires Enclosed In Cavities With Apertures［J］.Electromagnetics，2005，(25):655-678.

［8］ WEILAND T.On The Numerical Solution of Maxwell’s Equations and Applications in the Field of Accelerator Physics［J］.Partical Accelerator，1984，(15):245-292.

［9］ WEILAND T.Time Domain Electromagnetic Field Computation with Finite Difference Methods［J］.International Journal of Numerical Modeling，1996，(9):295-319.

［10］ 李德玺.圆柱坐标系有限积分方法仿真耦合腔高频特性［D］.成都:电子科技大学，2007.

［11］ TESCHE F M，LANOZ M V，KARLSSON T.EMC Analysis Methods and Computational Models［M］.New York:Wiley Interscience，1996:202-215.

［12］ 王建国，刘国治，周金山.微波孔缝线性耦合函数研究［J］. 强激光与粒子束，2003，15(11):1093-1099.