双/多基地雷达时间同步的一种新方法*
谢辉,谢军伟,冯广飞
(1.空军工程大学防空反导学院,陕西西安 710051;2.中国人民解放军驻七八六厂军事代表室,陕西西安 710043)
0 引言
在现代战争中,制空权的争夺已成为焦点,防空雷达始终在争夺战中扮演重要的角色。针对现有的单基地雷达,各种对抗措施如隐身技术、综合电子干扰、反辐射导弹和超低空突防等技战术手段已迅速发展起来。双/多基地雷达由于收发分置,在体制上天然具备了反隐身、抗干扰、抗低空突防和抗反辐射导弹的优势[1-3],与此同时也带来了收发站之间的同步问题,而时间同步是实现双/多基地雷达同步的关键技术之一。双/多基地跟踪雷达为了实现高精度的距离解算,要求时统的精度为数十纳秒以下,目前只有卫星双向中继法、GPS卫星授时、光纤通信和搬运钟能够满足精度要求[4-5],目前满足高精度时间同步要求且使用方便的授时系统是GPS授时,但在战时 GPS容易受到干扰[6-9],因此对不依赖于GPS的高精度时间校准技术进行研究是一个亟待解决的课题。
这里提出了一种新的时间同步校准方法。通过短波束或有、无源电视同步信号进行一次校时,达到基本对准的目的,精度可达1~5 ms[10-12]。在一次校时基础上,利用现代雷达大多具有多通道多目标跟踪能力的特点进行二次校时,通过接收站不同通道对同一目标进行跟踪,分别实施双基测量和单基测量,对双基和单基测量值进行最小二乘处理,求解出系统的时间同步误差,仿真结果表明单双基测量值比对可以达到高精度的时间同步。
1 基本原理
如图1是以接收站为中心的站心极坐标系,表示双基地雷达接收站、照射站和目标间的坐标关系,图中目标的坐标为 TG(εR,βR,RR),照射站大地坐标经坐标转换后,在以接收站为中心的站心极坐标系中的坐标为TX(ε0,β0,L),在双基平面内接收站目标视角为θR。

图1 双基地雷达接收站极坐标系Fig.1 Polar coordinate system for the receivers of bistatic radar
由图1几何关系可以得到:

新型雷达大多采用了相控阵技术,具有多目标跟踪能力,因而就可以使雷达接收站的2个目标通道同时对同一批目标进行跟踪,其中一个通道对目标的单基信号进行跟踪,另一个通道对双基信号进行跟踪。单基信号通道可以获得目标的高低角、方位角及单基距,双基信号通道可以获得含有时间同步误差的双基距。
目标在双基平面内,利用目标视角θR,基线距离L及目标到接收站的单基距RR,根据余弦定理,可求出目标到照射站的距离RT,将RR与RT求和,即可求出目标到收、发站的距离和为

设在第i时刻测得的目标单基距为RR(i),接收站测量得到的高低角为εR(i),方位角为βR(i),双基距为RS(i),进行系统误差补偿后,各测量分量为
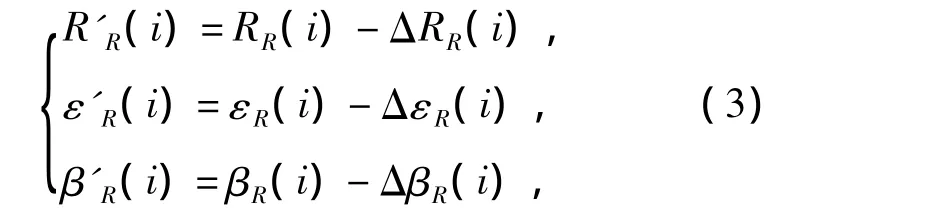
式中:ΔεR(i),ΔβR(i),ΔRR(i)为系统误差的补偿量,可事先得到,根据第i时刻系统误差补偿后的单基距、高低角和方位角,以及照射站在接收站站心极坐标系中的初始高低角、方位角,根据式(1)~(3),可求得第i时刻系统误差补偿后目标到收、发站的距离和为
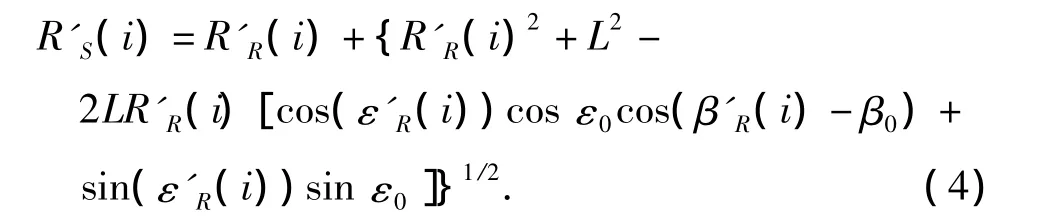
第i时刻目标双基信号通道测得目标双基距为RS(i),且第 i时刻双基距系统误差补偿量为ΔRS(i),可事先得到。设Δτ为收、发站的时间同步系统误差,c为光速。则经过双基距系统误差补偿和时间系统误差补偿后的实测双基距为

假设雷达进行了N次测量,可得N个R'S(i),R″S(i,Δτ),为了取得 Δτ的估值,由最小二乘原理应使式(6)达到最小。

式中:f(Δτ)为Δτ的二次函数,要使最小,即求导,令f'(Δτ)=0可解出关于 Δτ的解析式,而f″(Δτ)=c2N >0则证明最小二乘解存在,则 Δτ 为
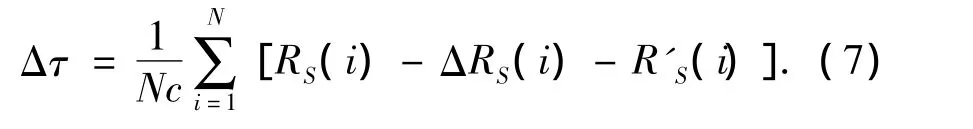
调整接收站同步脉冲的时延,即可实现收、发站的时间同步。如图2所示,当Δτ>0时,延时Δτ;当Δτ<0时,延时,T为雷达工作周期。

图2 目标测量实现时间同步示意图Fig.2 Sketch map of time synchronization realized by target measure
2 距离和解算误差及时间同步精度分析
在式(2)中,基线距离L及ε0,β0可由高精度大地测绘仪器测量求出,因此,距离和解算误差主要受接收站高低角εR,方位角βR和距离和RS测量误差决定,设 εR,βR,RR的均方根误差分别为 σεR,σβR,σRR。求 RS关于 εR,βR,RR的偏导,得距离解算误差为

根据式(2)和(8)可得到目标双基距及其定位精度。设照射站在接收站站心极坐系坐标为(0°,270°,40 km),即照射站位于接收站站心直角坐标系(-40,0,0)km,接收站位于直角坐标原点(0,0,0)。分别对目标高度为8 km和3 km时双基距解算精度进行仿真,坐标系取接收站站心直角坐标系±80 km范围内,仿真双基距解算误差如图3所示。
由图3可以得到,在某一高度上的等误差线曲线关于基线对称分布,在基线两侧区域,双基距解算误差较小,在垂直基线两侧空域,双基距解算误差相对变大;目标高度降低,双基距解算误差基本保持不变;利用单基距、高低角、方位角解算双基距具有较高的精度。
由式(7)可以看出,双基距解算误差与时间同步的精度存在对应关系,两者一一对应,成线性关系,如式(9)所示:


式中:σRS为距离和解算精度,单位为m;c为光速;Δτ'为时间校准误差,单位为ns。主要通过对双基距离和解算精度进行分析,以双基距解算精度反映时间校准精度。
绘单、双基目标测量与比对的时间校准精度曲线如图4所示。
如图4所示,由于双基距精度同时间同步误差成线性关系,因此,在双基距解算精度高的空域同步精度就高,双基距解算误差大的空域,相应时间校准误差就大。在给定角度误差为1',单基距误差为5 m的情况下,时间同步精度在整个空域内误差基本不大于50 ns。需要指出的是,此方法校准时间精度同雷达系统测角精度及单基距测量精度有关,测量精度越高,时间校准精度就越高。

图4 单、双基测量与比对时间校准精度(σεR= σβR=1',σRR=5 m)Fig.4 Time calibrating precision of monostatic,bistatic measure and compare(σεR= σβR=1',σRR=5 m)
3 仿真结果及分析
假设照射站和接收站的基线距离为40 km;目标作等高直线飞行,飞行高度为8 km,目标速度为420 m/s,航迹斜距范围10~40 km,航向角为7π/4,航路捷径为0;单基距经误差补偿后的系统误差设为2 m,起伏误差为5 m,高低角和方位角经误差补偿后的系统误差设为1',起伏误差为2',双基距离和误差补偿后的系统误差设为2 m,起伏误差为5 m。在第1次校时基础上设置不同时间系统误差,用最小二乘法求解时间同步误差,经过100次的蒙特卡罗仿真,结果如表1所示。
由表1仿真结果可以看出,在收、发站设置不同的时间系统误差条件下,可求解到较高精度的时间同步误差,校准精度可达50 ns左右。因此,基于单、双基测量和比对时间校准方法,可以获得较高校准精度,基本上与理论分析一致,说明该方法在理论上是可行的。但需要指出的是当系统误差补偿不完善时,校准的精度将变差,同时校准精度也与航迹的选择有关,为了得到高的时间同步精度,应选择定位精度高的航迹进行校准或利用已知目标进行时间校准。

表1 基于单、双基测量比对时间校准仿真结果Table 1 Time calibrating precision of measure and compare based on monostatic and bistatic
4 结束语
本文针对GPS容易受干扰的缺点,提出了先用短波或电视信号进行一次校时,再通过对目标双基测量,与单基测量值比对的二次校时方法。运用最小二乘方法建立目标函数,求解系统的时间同步误差,结果表明可以达到高的时间同步精度。验证了这种时间同步校准的方法在理论上是可行的,至于具体的实践可行性还需作进一步的试验和分析。
[1] 杨振起,张永顺,骆永军,等.双(多)基地雷达系统[M].北京:国防工业出版社,2001.
[2] 陈军,冯卫强,赵虎强,等.防空组网雷达“四抗”能力综合评估[J].指挥控制与仿真,2009,31(2):62-64.
[3] 何晓卒,刘昌镜.双基地雷达在抗反辐射武器系统中的应用分析[J].指挥控制与仿真,2009,31(3):35-38.
[4] 胡成.双多基地雷达同步技术研究与同步系统设计[D].成都:电子科技大学,2003.
[5] 王卿,宋铁成,奉媛.基于GPS技术进行精确授时的方法[J].2007,29(8):34-38.
[6] 谭显裕.GPS对抗技术的现状与发展[J].现代防御技术,2003,31(1):34-37.
[7] 王柏武,杨子杰,龙志,等.GPS在双(多)基地高频地波雷达中的应用[J].现代雷达,2005,27(5):65-68.
[8] 吴兴存,任宇飞,程乃平.GPS接收机中多径干扰的研究[J]. 现代防御技术,2008,36(4):123-127.
[9] 顾云涛,王忠,田海涛.GPS干扰与抗干扰能力分析[J].舰船电子工程,2011,31(2):62-63.
[10] 李学森,付庆霞.双/多基地雷达系统同步技术[J].舰船电子对抗,2007,30(4):50-53.
[11] 姜军,张小宽,李洪兵.利用共视比对解决雷达网时间同步方法[J].现代雷达,2009,31(3):70-72.
[12] 刘铭,龙光正,曹海江.组网雷达交叉定位模式下时间同步的目标定位[J].火力与指挥控制,2011,36(1):
160-162.

