基于蒙特卡洛法的钢管腐蚀结构可靠性研究

吴 迪 张志霞 张 艳

西安建筑科技大学 管理学院 （陕西 西安 710055）

基于蒙特卡洛法的钢管腐蚀结构可靠性研究

吴 迪 张志霞 张 艳

西安建筑科技大学 管理学院 （陕西 西安 710055）

钢管具有易于腐蚀的特性，所以研究钢管因腐蚀导致的结构失效具有重要的现实意义。根据埋地钢管的环向应力的变化，结合管道的几何尺寸、管道的腐蚀速率、管道的屈服强度等参数，基于蒙特卡洛法建立腐蚀钢管的可靠性模型，确定故障分布函数，对腐蚀管道的各个参数和失效概率进行分析和计算，并借助MATLAB工具完成整个仿真过程。

腐蚀钢管 蒙特卡洛法 失效率

目前，天然气长输管道的材质主要使用的是直缝钢管，其具有应力状态好、几何尺寸精度高、外防腐蚀效果好以及适于做内涂层减阻等特点，这符合日益增加的管道输送介质内压的要求。但是，钢管输送也存在缺陷，其最大的缺点是易于腐蚀。一般的天然气管道在敷设前都会进行防腐蚀处理，如果仅做简单处理，钢管在10～20a就会出现严重腐蚀，如果处理得当，可以将钢管的使用寿命延长至50～60年。所以，管道的抗腐蚀处理一直是保证钢管输送管道正常运行的关键性工作，这里在可靠性理论的基础上结合管道腐蚀特性进行失效可靠性分析。

1 腐蚀钢管的可靠性分析

钢管的机械可靠性主要取决于它的受力情况，导致管道失效的的主要受力包括轴向应力和环向应力[1]。轴向应力主要由温度、内压以及管道轴向摩擦所引起的；环向应力主要由内压、土体压力、地面车辆荷载所产生的。

管道在运行过程中，一般要承受外力、内压、温度等荷载，这些参数的随机性和变异性较大，很难确定其概率分布密度，所以为了便于分析，不考虑其他荷载的影响，仅分析因腐蚀导致的管道环向应力的变化。

对于具有腐蚀缺陷的管道，管道环向应力计算公式常用式（1）[2]。

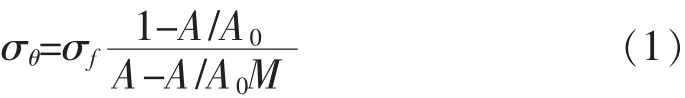
式中 σθ——管道环向应力,MPa；

σf——管道的流变应力,MPa；

A——管道腐蚀后，腐蚀缺陷的侧面投影面积，mm2；

A0——管道腐蚀处管道的原始截面积，mm2；

M——鼓胀因子。

其中，鼓胀因子的大小与L2/Dt密切相关，L表示腐蚀坑的最大长度（mm），t表示管道壁厚，D表示管道的外径，M可以表示为

在式（1）中，管道的流变应力 σf=kσy,σy是管道的屈服应力，k是系数。对于钢管，k通常取1.1或1.15[3]。管道腐蚀缺陷的侧面投影面积A=0.85dL,d是腐蚀坑的最大深度。那么，σθ可以表示为

对于腐蚀管道，壁厚t相对较小，且外径D和流体密度相对于流体压力也比较小的，那么腐蚀管道失效时的压力pθ和环向应力σθ的关系表示为

管材往往受管内输送介质和管外环境 （大气或土壤）的化学作用、电化学作用和细菌作用，对管材表面产生破坏，造成均匀腐蚀、局部腐蚀、点腐蚀、选择性腐蚀等腐蚀形式。因为腐蚀机理复杂，所以很难建立腐蚀确定性模型。在工程计算中，常用经验公式来表达管道腐蚀的发展过程，如使用幂函数[4]、线性函数、二阶段指数等表示腐蚀模型，为了简化计算，根据文献[5]的研究结果，腐蚀的速率是线性发展的。假定当前时刻检测的腐蚀管道的腐蚀缺陷的长度和深度分别为L0和d0，则服役到T时刻的腐蚀缺陷的长度和深度为

通过以上的分析可知，腐蚀管道的失效状态函数可以表示为

式中 pθ—表示钢管抵抗压力；

p0—表示流变压力。

将（4）式代入上式得腐蚀管道的失效状态函数表示

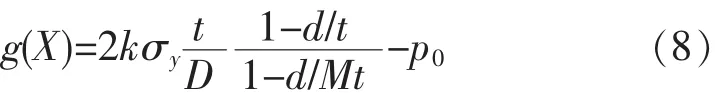
2 钢管可靠性算例

因腐蚀导致的管道失效是不确定的，主要是因为管道的几何尺寸、管道的腐蚀速率、管道的屈服强度等参数都是随机的。在这些参数中，有些可以通过文献参考获得其随机状态分布函数，有些则要采用数学建模的思想，假定其概率分布形式，本算例中是运行近30a的某天然气管道，管材采用16Mn螺旋焊管，所涉及到的参数主要取至参考文献[5]和[6]，见表1。假定各参数均为正态分布。

表1 某钢管随机参数

2.1 基于蒙特卡洛法建立模型

蒙特卡洛法是一种借助于概率化的数学模型而解决问题的统计定量方法[7]。利用蒙特卡洛法解决问题的基本思想是：首先建立与描述该问题有相似性的概率模型，并利用这种相似性把这个概率模型的某些特征（如随机变量的均值、方差）与数学计算问题的解答联系起来，然后对模型进行随机模拟或统计抽样，最终利用所得结果求出这些特征的统计估计值作为原来的数学计算问题的近似解。

利用蒙特卡洛法求解该问题的具体步骤如下：

Step1输入极限状态方程参数的算术平均值和变异系数（见表1），输入循环次数N=10 000；

Step2设置管道服役时间，T∈[30,50]；

Step3 将其代入（5）、（6）2 式，计算出当前时刻的 L和 d；

Step4求出各个自变量的值。

（1）确定 X=(x1,x2,x3,x4,x5,x6,x7)=(D,t,σy,d,L,Rd,RL）的故障分布函数：

各参数故障分布函数为

同理，F(x3)、F(x4)、F(x5)、F(x6)、F(x7)的故障分布函数代入均值和方差（变异系数即可）。

（2）生成0～1之间的均匀分布的随机数Kij(i=1,2,…7,j=1,2,…,n)，i表示参数下标，j表示循环系数。令Kij=F(xi),求出 j组x1,x2,x3,x4,x5,x6,x7的值。

Step5将上述产生的随机数代入式（8），若g(x)＜0，记为 n=1，否则，n=0；

Step6返回Step4继续执行，直到满足j=N为止；

Step7计算系统的失效率λ，λ(t)=n/N；

Step8返回Step2，计算下一次。

2.2 MATLAB实现蒙特卡洛法

整个求解过程借助MATLAB工具进行运算。利用MATLAB的强大数值计算功能，实现在MATLAB统计工具箱中采用蒙特卡洛直接抽样计算腐蚀钢管的失效概率[8]。

MATLAB的实现步骤如下：

Step1设置管道服役时间，T∈[30,50]；

Step2利用正态随机数发生指令x=normrnd(mu,sigma,N,1)；分别产生N组随机变量数xi(i=1,2,3,4,5,6,7)；

Step3利用MATLAB的运算功能，将产生的随机数 xi(i=1,2,3,4,5,6,7)代入功能函数g(X1,X2,…X7)中，通过运算，得到功能函数值g(X)；

Step4统计功能函数值g(X)的元素g(j)，其中大于零的元素个数为n，则失效概率为λ(t)=n/N，可靠度为 P=1-λ(t)；

Step5返回Step2，计算下1a。

经过运算得到时间与失效率λ的关系图（如图1所示）。随着天然气管道服役时间的增加，失效概率也逐渐增大。

2.3 钢管的敏感性分析

对腐蚀钢管进行参数敏感性分析的目的是为了得到对失效率影响最大的几个参数，为防止钢管失效找到关键因素。通过比较各个参数的敏感性指标的相对大小，找出影响结构可靠性的关键问题，为提高结构可靠性提供了比较准确的参数。钢管的参数共有以下8个：管道外径D、管道壁厚t、管道内压p、管道屈服强度 σy、腐蚀深度 d、腐蚀长度 L、深度腐蚀速率Rd、长度腐蚀速率RL。假设钢管的第一次检测时间是T0=20a，那么钢管在服役30a、40a、50a时的失效率λ随上述8种参数的改变而发生改变。

腐蚀钢管的失效率随着管道外径D、管道内压p、腐蚀深度d、腐蚀长度L、深度腐蚀速率Rd、长度腐蚀速率RL这6个参数的增加而增大；钢管服役时间的增加，其失效率也随之增大。腐蚀钢管的失效率随着管道壁厚t，管道屈服强度σy的增加而减小。由此可以得出：随着钢管腐蚀深度和腐蚀长度的增加，管道的安全性能显然是变坏，而且随着服役年限的增加，管道的安全性能会越差；随着管道外径的增加，管道腐蚀部分所承受的内压将引起环向压力的增加，管道的安全性能变坏；随着服役时间的增加，深度腐蚀速率Rd的变化趋势比长度腐蚀速率RL的变化趋势要更为明显。通过上述分析，影响钢管失效的主要因素是管道壁厚t、管道内压p、腐蚀深度d、腐蚀长度L、深度腐蚀速率Rd。

3 结 论

钢管腐蚀失效因素众多，失效机理复杂，难以用确定的解析结构模型进行结构可靠性分析，所以选用蒙特卡洛模拟法对因钢管腐蚀导致的可靠性进行研究。结合管道的几何尺寸、管道的腐蚀速率、管道的屈服强度等参数，对腐蚀钢管的抵抗压力的变化进行分析。通过MATLAB工具，利用MATLAB强大的运算功能，实现了蒙特卡洛法模拟，进而对腐蚀钢管进行参数敏感性分析，找出了影响钢管失效的关键因素。通过分析论证：随着天然气管道服役时间的增加，失效概率也逐渐增大；影响钢管失效的主要参数有管道壁厚t、管道内压p、腐蚀深度d、腐蚀长度L、深度腐蚀速率Rd。这一模型的建立，为提高结构可靠性提供了比较准确的参数。也为今后降低腐蚀钢管的失效率及制定钢管的腐蚀防护措施，提供了重要的参考价值。

[1]帅键,于桂杰.管道及储罐强度设计[M].北京:石油工业出版社,2006.

[2]Mok DRB,Pick RJ,Glover AG.Behavior of line pipeline pipe with long external corrosion[J].Materials Performance,1990(5):75-79.

[3]Hopkins,P;Jones,D.G.A study of the behavior of long and complex-shaped corrosion in transmission pipelines[A].In Proc.11th Int.Conf.on Offshore Mechanics and Arctic Engineering[C],Vol.V,Part a,ASME,1992:211-217.

[4]Amirat,Mohamed-Chateauneuf and Chaoui.Reliability assessment of underground pipelines under the combined effect of active corrosion and residual stress[J].International Journal of Pressure Vessels and Piping,2006,83(2):107-117.

[5]赵事,蒋晓斌,高惠临.腐蚀管道的失效概率和剩余寿命预测方法[J].油气储运,2006,25(12):28-31.

[6]邵煜.埋地管道的失效机理及其可靠性研究[D].浙江:浙江大学,2008:49-66.

[7]Wu Liu,Yi Liu,etc.Evaluation of Aseismatic Fuzzy Reliability for Gas Field Pipeline Network Based on Monte-Carlo Simulation[C].ICPTT 2009?2009 ASCE,2009,12:1184-1196.

[8]陈健,盘钦卿,王卫星.MATLAB实现蒙特卡洛法在箱梁施工可靠度中的应用[J].重庆工商大学学报,2011,28(1):90-93.

Steel tube has the property easy to be corroded,so it is significant to make a research on the structure failure of steel tube caused by corrosion.According to the change of circumferential stress of buried pipes,combined with the parameters like the physical dimension,the corrosive rate,the yield strength of pipeline,the reliable model of corroded steel tube is established based on Monte Carlo Approach,together with the determination of fault distribution function.Meanwhile,various parameters and failure probability of corroded pipeline are calculated and analyzed,and the entire simulation process is finished by means of MATLAB.

corroded stress;Monte Carlo Approach;failure rate

吴迪（1988-），女，西安建筑科技大学在读研究生，主要从事系统工程与计算机应用。

��尉立岗

2012-03-06▏