基于灰色BP网络的卫星钟差预报

郭振华，韩保民，赵金生

（1.山东理工大学 建筑工程学院，山东 淄博 255091；2.淄博职业学院 建筑工程学院，山东 淄博 255314）

目前，国际GPS服务组织（IGS）的几个数据分析中心已经具备提供高精度的GPS卫星星历的能力，但都是事后处理结果.并且星载GPS原子钟频率高、非常敏感、极易受到外界及其本身因素的影响［1］，从而很难掌握其复杂细致的变化规律，因此，进行卫星钟差预报的研究是非常有意义的［2］.

灰色预测模型是20世纪80年代发展起来的非线性外推类预测方法，其实用性强，所需数据量较少，建模灵活方便，预测精度较高，从而在社会科学和自然科学各领域得到广泛应用；而神经网络具有并行计算、分布式信息存储、容错能力强、自适应学习功能等优点，在处理复杂的人工智能和非线性问题上表现出极好的效果［3－5］.本文应用灰色模型GM（1，1）和BP神经网络模型对卫星钟差进行预报和精度分析，可为卫星钟差序列预报提供借鉴和参考.

1 模型原理

1.1 灰色模型GM（1，1）

设有变量X（0）的原始数据序列［6］:对原始数据序列进行1次累加生成新灰色模块

由新灰色模块X（1）构成的微分方程为

求解微分方程，求得离散解为

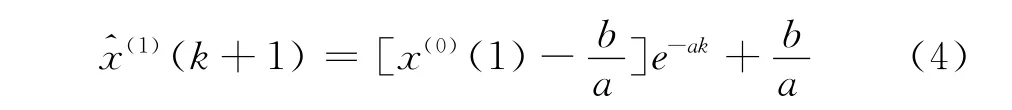
式中k为参与预报的原始数据个数.

最终预测公式可表示为

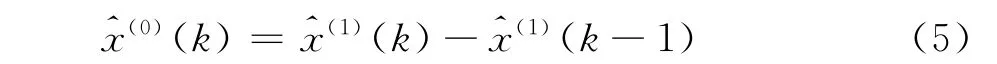
式中k＝1，2，3…….

1.2 BP网络模型

BP神经网络模型［7］英文名称为back propagation network，也称为反向传播神经网络，由输入层、隐含层以及输出层三部分组成，其中隐含层可以一层或为多层，相邻的上下层之间通过各神经元来全部连接，但是每层的各神经元之间则没有连接，可说是目前神经网络中应用最为广泛的预测模型，其网络模型如图1所示.

图1 BP网络模型

BP神经网络的核心思想是:通过大量的反复训练学习，来不断调整网络中的各连接权重，直到网络的输出与期望的输出趋于一致或差值小于某个规定值，即可得到理想的输出结果.

2 方案设计及流程

灰色模型理论现在已经十分成熟，应用于包括卫星钟差时间序列预报在内的很多领域，预报结果比较平稳，而且精度很高.在这里将经过粗差剔除后的所有卫星钟差数据直接采用灰色GM（1，1）模型预报，作为与BP神经网络模型预报的参考.

在采用BP神经网络模型预报之前，首先要对模型进行处理，既确定最佳的隐含层神经元个数.在这里将经过粗差剔除后的所有卫星钟差数据一分为二，编写程序利用循环不断修改BP神经网络模型隐含层神经元个数对先前大半部分数据进行预报，并与后面的另一部分数据进行比较，通过分析RMS值，选取RMS值最小时对应的隐含层神经元个数作为最佳隐含层神经元个数.此外，模型中采用的最小均方误差要在训练中进行调试和相应设置，经过反复调试找到卫星钟差预报时最佳最小均方误差进行约束.然后就可采用最佳隐含层神经元个数的BP神经网络模型对所有卫星钟差数据进行预报，分析获得的残差数据，并且与灰色GM（1，1）模型比较，得出相应结论.

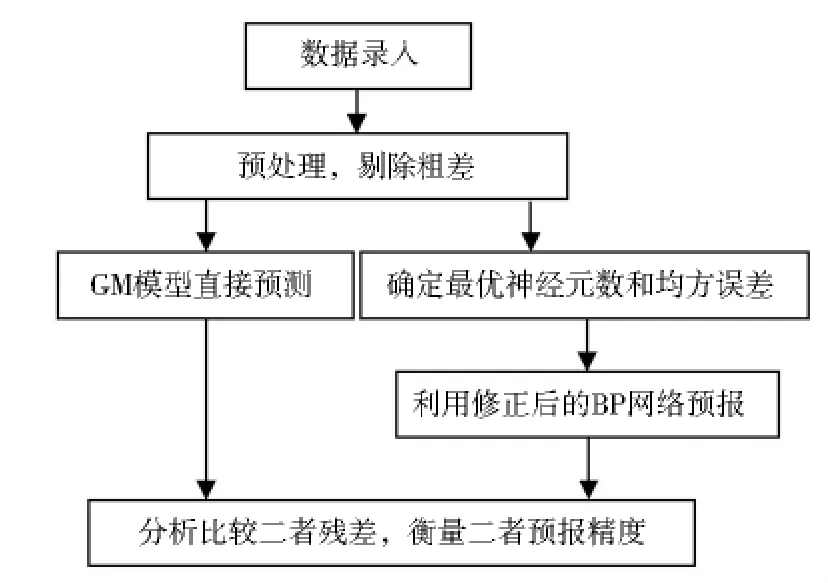
图2 钟差预报流程图

3 算例及分析

3.1 算例1

基于少量钟差数据预报:本算例采用IGS提供的2009年5月23日6号和10号卫星钟差数据进行预报，其时间间隔为5min的，用其中1至2时共1小时的12个历元卫星钟差数据来预报随后2个小时的卫星钟差，然后将预报值与标准数据比较，分析两种模型的预报精度，结果见图3和表1.

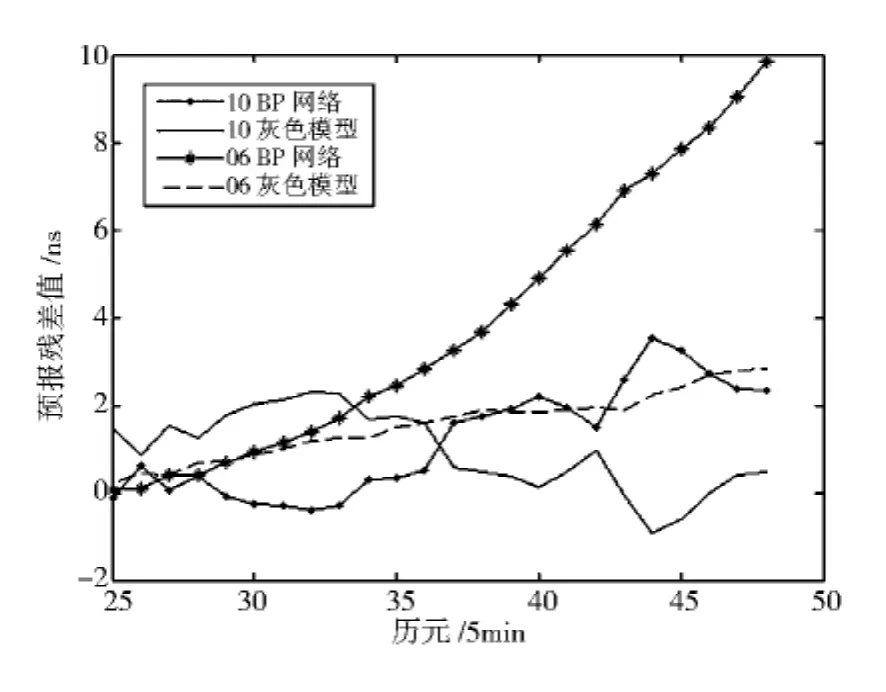
图3 基于少量钟差数据预报图形

从图3和表1，我们能够发现对于两颗卫星采用少量钟差数据进行两小时卫星钟差预报，两种方法的预报效果不同.灰色GM（1，1）模型虽起初就下降不少，但是后期较BP模型平稳，误差较小.这里灰色模型建模所需数据量少，建模速度快，预报精度较高的功能得到充分展现.而BP网络模型前期几个历元预报精度较高，但后来精度下将明显，尤其对6号卫星的预报效果不佳，分析原因:建模数据不充足，6号卫星个别数据质量不佳.

表1 少量钟差数据预报的残差统计 ns

表2 大量钟差数据预报的残差统计表 ns

3.2 算例2

基于大量钟差数据预报:算例说明同算例一，所不同的是，在算例2中，用0至2时共2个小时的数据预报随后2个小时的卫星钟差，算例结果见图4和表2.

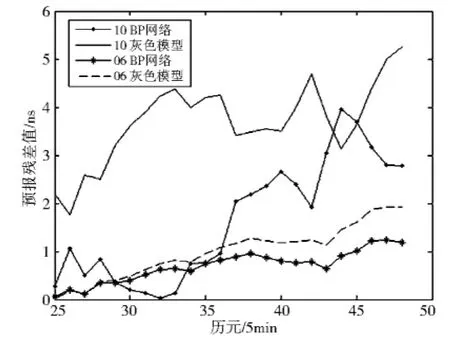
图4 基于大量钟差数据预报图形

从图4和表2，可以看到对这两颗颗卫星采用大量钟差数据进行两小时卫星钟差预报时，对6号卫星预报两种模型都能达到很好的精度，预报精度控制在2ns以内.尤其是BP网络模型确定好隐含层神经元数及最小均方误差后，经过反复训练调试，预报精度相对于GM（1，1）提高显著，对大量数据预报情况比少量数据预报要好.这归功于BP网络模型的联想记忆功能，反复训练，预报值能够得到很有效预报，使预报精度提高了很多.对10号卫星，灰色模型误差较大，起始历元的预报就有不小偏差，BP网络模型效果要好些，而两模型对大量数据预报精度比少量数据预报时精度都有所降低，分析原因主要是数据质量问题:大量数据预报时，10号卫星个别历元数据质量不佳.此外，我们能够发现不同的模型对不同卫星、不同类型的数据适宜性不同，有必要去做大量的研究和有效的预计.

3.3 算例3

基于IGU超快速钟差数据预报:利用IGU中提供的时间间隔15min的0至6时6号和10号卫星的超快速卫星钟差进行未来6个小时的卫星钟差预报，并分析预报精度，计算结果见图5和表3.

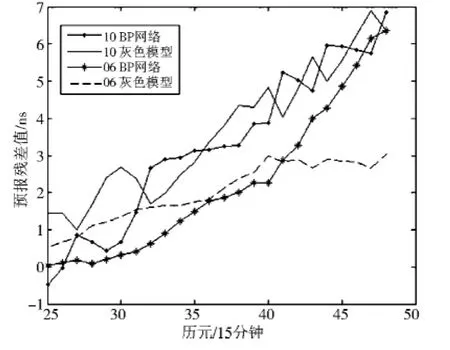
图5 基于IGU超快速钟差数据预报图形

从图5和表3中，可以看到在IGU超快速钟差的预报中两种模型具有很好的实际有效性.GM（1，1）模型起始预报精度稍差，但到后期累积趋势较缓慢.BP神经网络模型起始预报效果较好，精度较高，这是BP神经网络模型的一大优势，但后期稳定性不算很好，从6号卫星就能看出来.所以，短期卫星钟差预报中，事先做好预计，对于哪颗卫星哪种模型更有效；也将两种模型结合应用，找出拐点，优势互补，发挥二者特长，进而获得好的预报效果，体现实用价值.

表3 IGU超快速钟差预报的残差统计表 ns

4 结束语

GPS卫星原子钟频率高、敏感以及易受到外界及其本身因素的影响，不同的模型对不同的卫星适宜性不同.灰色GM（1，1）模型预报精度较高并且稳定，而神经网络基于自身的联想记忆能力，具有较好学习逼近非线性映射的功能，且平滑效果较好，适合卫星钟差序列这种非线性时间序列的预报.当原始钟差数据充足时，BP神经网络可以充分利用数据信息建模，预报精度很高.IGU超快速钟差的预报中，可以将BP神经网络和灰色GM（1，1）模型联合应用，优势互补，进而提高卫星钟差预报的精度.

［1］崔先强，焦文海.灰色系统模型在卫星钟差预报中的应用［J］.武汉大学学报:信息科学版，2005，30（5）:50－54

［2］韩保民.精密卫星钟差加密方法及其对星载GPS低轨卫星定轨精度影响［J］.武汉大学学报:信息科学版，2006，31（12）:1075－1078.

［3］郭承军，腾云龙.基于小波分析和神经网络的卫星钟差预报性能分析［J］.天文学报，2010，51（4）:395－403.

［4］陈炳志.基坑变形灰色人工神经网络预测模型及其应用［M］.Natural Science，2010，29（5）:53－57.

［5］王秀.灰色组合预测模型应用研究［J］.长沙大学学报，2010，24（2）:24－27.

［6］邓聚龙.灰色系统基本方法［M］.武汉:华中工学院出版社，1987.

［7］施鸿宝.神经网络及其应用［M］.西安:西安交通大学出版社，1993.