基于ABAQUS的黏弹性人工边界在重力坝分析中的应用

郝明辉，张艳红，陈厚群

（中国水利水电科学研究院 工程抗震研究中心，北京 100048）

1 研究背景

坝体-地基动力相互作用是影响结构地震反应重要因素之一，这种动态相互作用主要包括地基对结构体系动态特性的影响以及结构对地震动输入的影响，其中主要是地震波能量向远域地基的逸散。所以，在坝与基岩地震动力相互作用分析中，正确实现地震动的输入和地基辐射阻尼的模拟是十分重要的。采用数值离散方法分析地基基础时要处理地基无限域问题，在动力分析中目前得到广泛应用的主要有黏性边界、透射边界和黏弹性边界[1-3]等，其中黏弹性边界是在黏性边界的基础上再在人工边界上设置弹性元件，其克服了黏性边界的低频失稳问题，能够模拟远域地基的弹性恢复性能，具有良好的低频和高频稳定性，并且无需像透射边界那样增加大量的边界节点和单元，在实际工程中得到广泛的应用。

ABAQUS软件[4-5]已在大坝的动态非线性分析中得到了广泛的应用。本文将黏弹性边界理论应用于非线性有限元软件ABAQUS中，对重力坝-地基系统进行地震动力响应数值分析。

2 二维黏弹性边界

黏弹性人工边界可以等效为在人工截断边界上设置连续分布的并联弹簧-阻尼器系统，其中弹簧刚度系数和阻尼器的阻尼系数可以归结为：

式中：ρ、G分别为介质的质量密度和剪切模量；R为散射波源到人工边界的距离；c为介质中的波速，法向人工边界c取P波波速cP，切向人工边界取S波波速cS；α为参数，α参照文献[6]取值。

当α取零或R趋于无穷大时，刚度系数Kb=0，黏弹性人工边界退化为黏性人工边界。

当黏弹性边界转化为弹簧-阻尼器单元时，黏弹性边界完全吸收计算区域的外传散射波，人工边界节点承受的就是地震自由场运动，地震的输入问题转化为在人工边界节点上作用自由场运动的问题，自由场运动可转化为人工边界节点上的等效节点力处理[7]。

式中：Ab为边界节点的影响面积；n为边界外法线方向余弦向量；Kb为刚度阵；Cb为阻尼阵。

由弹性力学可知：

假设底边界入射位移波u=u（0t），v=v（0t），根据一维波动理论，自由场在任意位置h任意时刻t有：

式中：H为底边界到地表的距离；h为人工边界节点到底边界的距离。

由于底面和4个侧面的外法线方向余弦向量n以及弹簧刚度Kb、阻尼系数Cb有所不同，故分别讨论。

（1）底边界。n=[0，-1]T。

将式（4）、式（6）代入式（2）并将式（3）、式（5）以及n=[0，-1]T一并代入式（1）可得：

其中，等效节点力的上标代表人工边界节点所在边界面的法线方向，与坐标轴方向一致为正，相反为负；下标表示分量方向。

（2）侧边界。

（a）x=0：n=[-1，0]T。同理可得：

（b）x=xb：n=[1，0]T。同理可得：

在有限元软件ABAQUS隐式求解器中，黏弹性边界是通过在人工截断边界处施加一系列的弹簧单元（Spring1）和阻尼单元（Dashpot1）实现的，inp文件输入*Element，type=Spring1/Dashpot1，elset=D21（定义接地弹簧/阻尼单元类型，将一系列节点创建为该类型单元，并将该一系列单元定义一个单元集合D21），地震动输入的实现方式通过关键词*Amplitude和*Cload实现。

3 实例验证

从二维半无限空间中截取6m×50m的有限范围，顶端自由，用1m×1m的单元离散，其底面和2个侧面连接黏弹性边界。材料弹性模量为24MPa，剪切模量为10MPa，泊松比为0.2，质量密度为1 000kg/m3。底边界，垂直向上入射x方向单位脉冲剪切位移波和y向的单位脉冲压缩位移波，则位移响应为：

其中：f=0.4，0≤t≤0.25。

图1给出了黏弹性边界计算得到的模型底部、中部、顶部的水平向和纵向位移响应，可以看出波由底部向上传播并在自由地表发生反射，且自由地表处的总场位移幅值是输入波幅值的两倍。由图1可知本文的计算结果和理论解吻合的较好，证明该方法的正确性和有效性。

4 重力坝动力响应计算

图2是Koyna坝体-地基有限元计算网格。坝高103m，坝顶宽14.8m，坝底宽70m，坝段厚16m，在坝高66.5m处，下游坝面的坡面发生突然改变。坝体混凝土材料参数E=31027MPa，μ=0.15，ρ=2643kg/m3。动态拉伸屈服强度σt=2.9MPa，抗压强度σc=24.1MPa，阻尼C=αM+βK，α=0，β=0.00323。图3给出的是拉伸屈服应力、拉伸损伤变量和开裂位移之间的关系。另外，由于混凝土抗压强度一般较大，故没有考虑压缩引起的损伤。坝基在深度方向和上、下游方向都取2倍的坝高，基岩弹性模量E为2.5×104MPa，泊松比μ为0.25，密度ρ为2 500kg/m3。静态荷载主要考虑自重和静水压力。实测地震波如图4所示。库水动水压力对大坝地震响应的影响按照Westergaard附加质量法计入。

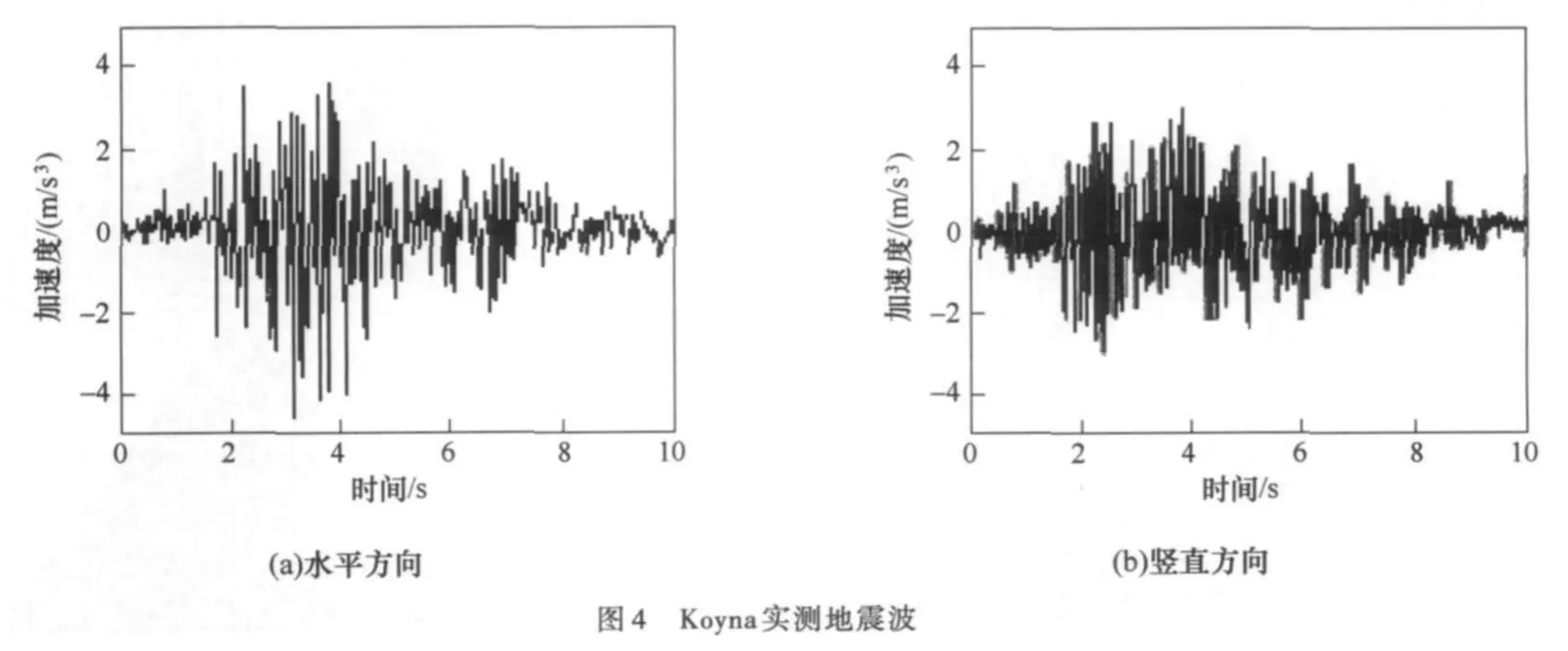
为了验证本文提出地震波输入方法的正确性，首先分析在没有坝体的情况下地基的动力反应。以图4所示地震波折半后作为人工边界上输入的地震波，假设地基为弹性均匀无阻尼的岩石地基，因此自由地表的响应幅值为输入波的两倍，见图5。

本文首先采用无质量地基模型进行地震响应分析。另外，考虑到无质量地基模型无法计入地震动能量向远域地基逸散的辐射阻尼效应和地基质量的影响，还将采用弹簧单元和阻尼单元实现黏弹性边界，并利用本文方法输入地震动来进行地震响应分析，以考察辐射阻尼效应对大坝地震响应的降低程度。

图6、图7是分别采用无质量地基模型和黏弹性边界计算得到的坝体损伤情况。由图可知，采用黏弹性边界输入地震波后，坝体相同部位出现损伤的时间有所滞后，这是由于地基的弹性关系，坝体自振频率变小，相应的振幅也变小，损伤出现的时间要晚一点。由于考虑了地基的弹性和辐射阻尼效应，坝体整体损伤情况减轻，坝体折坡处和坝堹部位与实际震害更加接近。坝堹部位的损伤在实际震害中也是不存在的，本文为了简化凸显边界的影响，地基采用了线弹性模型，未考虑地基非线性的影响，当考虑地基的非线性影响时坝堹部分的损伤是不存在的。

表1是坝体不同关键破坏部位损伤程度定量的描述，以损伤单元网格数占该部位整体网格数的比例计算得到，其中坝堹部位范围在0～4.589m处，上游坝腰范围在66.5～76.031m，下游折坡部位范围在52.23～70.67m，由表1可知，采用黏弹性边界后坝体损伤情况减轻，且与实际震害更加接近。

表1 坝体不同部位损伤程度

5 结论

坝体-地基动力相互作用是影响结构地震反应重要因素之一，这种动态相互作用主要包括地基对结构体系动态特性的影响以及结构对地震动输入的影响，其中主要是地震波能量向远域地基的逸散。本文采用了黏弹性边界，克服了黏性边界的低频失稳问题，能够模拟远域地基的弹性恢复性能，具有良好的低频和高频稳定性，并在非线性有限元软件ABAQUS软件上成功实施，经与理论解的结果对比，具有较高的求解精度。本文以典型的Koyna重力坝地震反应分析为例，比较了黏弹性边界与传统的固定边界无质量地基的计算结果。利用混凝土损伤模型对Koyna重力坝遭遇强震时震害现象进行了初步分析，得到了大坝下游折波处与实际遭受的地震破坏现象和破坏程度基本一致的结论。

[1]刘云贺，张伯艳，陈厚群.拱坝地震输入模型中黏弹性边界和黏性边界的比较[J].水利学报，2006，37（6）：758-763．

[2]谷音，刘晶波，杜义欣.三维一致黏弹性人工边界及黏弹性边界单元[J].工程力学，2007，24（12）：31-37．[3]廖振鹏.工程波动理论导引[M].北京：科学出版社，1996．

[4]Getting Started with Abaqus（interactive edition）[R].ABAQUS，INC，2009．

[5]王金昌，陈页开.ABAQUS在土木工程中的应用[M].杭州：浙江大学出版社，2006．

[6]李彬.地铁地下结构抗震理论分析与应用研究[D].北京：清华大学，2005．

[7]何建涛.地震作用下大坝-地基体系的损伤破坏研究[D].北京：中国水利水电科学研究院，2010．