例谈反比例函数的综合应用

☉江苏省常州市新北区实验中学 倪 枥

聪明、细心的同学会发现，在日常生活中存在着许多两个量之间具有反比例关系的例子.学习数学的目的是“学以致用”，现从反比例函数与一次函数、不等式、简单的几何知识、相关物理知识的综合应用这些方面举例分析，供同学们参考.

一、数学学科内知识间的综合应用

例1 如图1所示，A为反比例函数图像上的一点，AB垂直于x轴，垂足为B.若△AOB的面积为3，则反比例函数的解析式是什么？

分析：因为点A在反比例函数第二象限的图像上，所以，由三角形面积公式可求得k，从而求出反比例函数解析式.

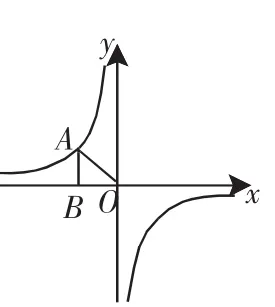
图1

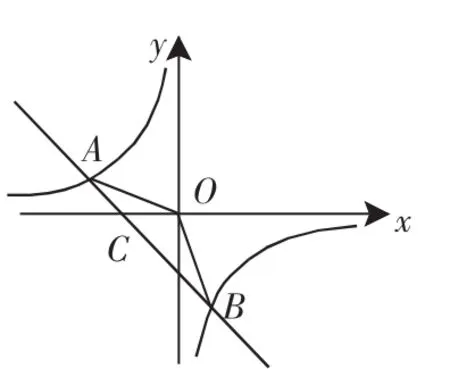
图2

解：因为函数图像分布在第二、四象限，所以k<0.

所以xy=－6=k.

例2 如图2，已知A（－4，n），B（2，－4）是一次函数y=kx+b的图像和反比例函数的图像的两个交点.

（1）求反比例函数和一次函数的解析式.

（2）求直线AB与x轴的交点C的坐标及△AOB的面积.

（请直接写出答案）.

分析：由于B点在反比例函数图像上，由反比例函数定义得m=－8，从而求出A点坐标，再用待定系数法求出一次函数解析式.根据数形结合的思想，求出△AOB的面积以及求方程的解和不等式的解集.

所以n=2.所以A（－4，2）.

因为y=kx+b经过A（－4，2），B（2，－4），

所以一次函数的解析式为：y=－x－2.

（2）因为C是直线AB与x轴的交点，

所以当y=0时，x=－2.

所以点C（－2，0）.

所以OC=2.

（3）x1=－4，x2=2.

（4）－42.

二、反比例函数与物理知识的综合应用

例3 一人站在平放在湿地上的木板上，当人和木板对湿地的压力一定时，随着木板面积S（m2）的变化，人和木板对地面的压强p（Pa）将如何变化？如果人和木板对湿地地面的压力为600N，回答下列问题：

（1）用含S的代数式表示p，p是S的反比例函数吗？为什么？

（2）当木板面积为0.2m2时，压强是多少？

（3）如果要求压强不超过6000Pa，木板面积至少要多大？

（4）画出相应的函数图像.

分析：根据两个变量之间关系确定两个变量之间的函数关系式，首先要判断它属于哪一类函数，然后根据实际意义并注意自变量的取值范围，进而作出正确的函数的图像.

解：随着木板面积S（m2）变小（大），压强p（Pa）将变大（小）.

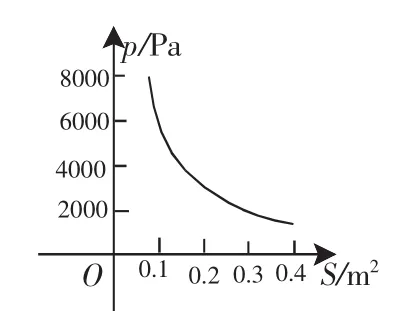
图3

（4）函数图像如图3所示.

例4 要求取消市场上使用杆秤的呼声越来越高.原因在于，一些不法商贩在卖货时将秤砣挖空，或更换较小秤砣，使砣变轻，从而欺骗顾客.

（1）如图4所示，对于同一物体，哪个用了较轻的秤砣？

（2）在称同一物体时，秤砣到支点的距离y与所用秤砣质量x之间满足_____________关系.

（3）当砣变轻时，称得的物体变重，这正好符合哪个函数的哪些性质？

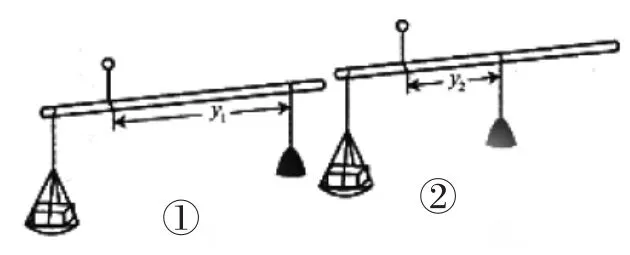
图4

分析：设重物的质量为G（定值），重物的受力点到支点的距离为l（定值），图4①、图4②中y1、y2分别表示秤砣的受力点到支点的距离.根据杠杆原理得：物体的质量（G）与阻力臂（l）的乘积等于秤砣的受力点到支点的距离（y1或y2）与秤砣质量（x）的乘积.

解：（1）因为Gl为定值，xy=Gl，且y1>y2，所以x1

（2）因为xy=Gl，所以y与x满足反比例函数关系.

（1）学生在调查中提出既希望能在课堂内对教材中的文化信息进行拓展讲解，也希望能够对照讲解相关的中国文化知识，以应对英语四、六级考级的建议。笔者在课堂教学过程中，从教材文本入手，一面讲授语言知识，锻炼语言能力，一面深挖教材资源，补充必要文化知识讲解和练习，活用教材。

三、反比例函数与生活知识的综合应用

例5 水产公司有一种海产品共2 104千克，为寻求合适的销售价格，进行了8天试销，试销情况如下表：

第1天第2天第3天第4天第5天第6天第7天第8天售价x(元/千克) 400 300 250 240 200 150 125 120销售量y(元/千克) 30 40 48 50 60 80 96 100

观察表中数据，发现可以用反比例函数刻画这种海产品的每天销售量y（千克）与销售价格x（元/千克）之间的关系.现假定在这批海产品的销售中，每天的销售量y（千克）与销售价格x（元/千克）之间都满足这一关系.

（1）写出这个反比例函数的解析式，并补全表格.

（2）在试销8天后，公司决定将这种海产品的销售价格定为150元/千克，并且每天都按这个价格销售，那么余下的这些海产品预计再用多少天可以全部售出？

（3）在按（2）中定价继续销售15天后，公司发现剩余的这些海产品必须在不超过2天内全部售出，此时需要重新确定一个销售价格，使后面两天都按新的价格销售，那么新确定的价格最高不超过每千克多少元才能完成销售任务？

分析：反比例函数是日常生活和生产实践中应用十分广泛的数学模型，要能够根据这个数学模型解决实际问题.

填表如下：

第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天售价x(元/千克) 400 300 250 240 200 150 125 120销售量y(元/千克) 30 40 48 50 60 80 96 100

（2）2 104-（30+40+48+50+60+80+96+100）=1600，

即8天试销后，余下的海产品还有1600千克.

1600÷80 =20 ，所以余下的这些海产品预计再用20天可以全部售出.

（3）1600-80×15=400，400÷2=200.

即如果正好用2天售完，那么每天需要售出200千克.

所以新确定的价格最高不超过60元/千克才能完成销售任务.

总之，学生要了解反比例函数是日常生活和生产实际中应用十分广泛的数学模型，掌握生活中有一类两变量的乘积为定值的实际问题可转化为反比例函数问题来解决的思想方法，从而不断提高自己运用数学方法分析、解决实际问题的能力.