非共沸混合工质流动沸腾参数计算方法研究

陈高飞，公茂琼，吴剑峰，汪胜

（中国科学院理化技术研究所低温工程学重点实验室，北京 100190）

非共沸混合工质流动沸腾参数计算方法研究

陈高飞*，公茂琼，吴剑峰，汪胜

（中国科学院理化技术研究所低温工程学重点实验室，北京 100190）

分析了非共沸混合工质流动沸腾过程与纯工质不同的特性，使用相平衡和热焓计算相结合的方法，研究了非共沸混合工质流动过程中的热物性参数，状态参数和流动参数的计算获取，给出了详细的计算步骤及相关计算式，为准确获取非共沸混合工质在流道中各局部点的参数提供了一种切实可行的计算方法。

非共沸混合工质；流动沸腾；两相流；相平衡计算

0 引言

经过多年的发展，非共沸混合制冷剂已经应用于多种制冷和热泵系统。使用非共沸混合工质作为制冷剂的节流制冷技术已成为80-230 K温区的主要制冷技术[1]。此外，采用非共沸混合工质的单级压缩热泵具有结构简单，制造成本低，运行调节简单，适用温区广且热力效率高等优点[2]。

与纯工质相比，混合工质在热系统中的应用需要更多更复杂的机理研究，其中涉及到相平衡问题，浓度变化问题，以及混合工质相变过程涉及的物性变化问题等。传热研究是直接影响系统设计和应用的重要课题。非共沸混合物饱和流动沸腾传热测量和计算与纯工质有很大的不同。Thome[3]在其综述文中指出，已发表的很多关于非共沸混合物流动沸腾的文献中，传热测量和计算不规范，给工业应用带来了很多困惑并造成了不必要的麻烦。特别是，很多学者直接用计算纯工质流动沸腾传热的方法来计算非共沸混合物。相平衡计算的缺失，会使获得的传热系数存在显著偏差。已有文献讨论过非共沸混合物流动沸腾的局部参数计算问题，但还没有见到针对各参数计算方法研究的完整和详尽论述。

为使非共沸混合物流动沸腾传热测量和计算更加精准易用，本文使用相平衡和热焓计算相结合的方法，研究了包括混合物热物性参数，两相平衡状态参数和流动参数在内的各参数的计算获取，并给出了详细的计算步骤及相关计算式。

1 非共沸混合物流动沸腾传热特性

在非共沸混合物的沸腾过程中，低沸点组分更加容易蒸发，所以在加热的管道中，沿着流动的方向，二元混合物中的低沸点组分在液相中所占的摩尔比例逐渐降低，而其在汽相中所占的摩尔比例则相应增大。对于三元混合物，泡点温度排在中间的那种组分则有可能加剧沸腾，也可能减弱沸腾，取决于其纯工质在该压力下的沸点是低于还是高于三元混合物的泡点。非共沸混合物的这种特性会使其在加热管道中流动时，混合物的汽液相各热物性参数沿着流动方向持续变化，且不能单纯使用循环系统内非共沸混合物总的组分比计算获得。

此外，对非共沸混合物饱和流动沸腾传热影响更大的是其沸点温度的变化。液体混合物处于某压力下开始沸腾的温度，称为该压力下的泡点温度（Tbub）；气体混合物处于某压力下开始凝结的温度，称为该压力下的露点温度（Tdew）。与纯工质不同，非共沸混合物的泡点温度低于它的露点温度。但是，非共沸混合物的传热系数与纯工质一样通过式（1）获得：

其中，Tw是加热流道内壁面温度；对于纯工质，Tbub是对应压力的饱和温度，而对于非共沸混合物，Tbub是对应压力下混合物液体的泡点温度。当汽相和液相中的摩尔组分比例沿着管道流动方向发生变化的时候，局部的泡点温度Tbub也会随之变化。随着沸腾的进行，低沸点组分在液相中所占比例逐渐降低，相应的Tbub则逐渐升高。此时，泡点温度不能单独通过压力计算获得。因此，在计算非共沸混合物流动传热系数之前，首先要获得它的泡点温度。直接在流道不同处进行取样测量存在难度，同时也可能会破坏管内流体的流动。本文以 CSD状态方程和热能方程为计算基础，通过相平衡和热焓计算获取流道沿程各局部点的混合物两相流动的汽液相组分比和质量含气率，进而获得其泡点温度及其它相关参数。

2 混合工质热物性计算

对于非共沸混合工质饱和流动沸腾，式（1）中传热系数的计算并不直接用到相关的热物性参数，但在热焓计算中，会用到局部混合物的液相和汽相焓值，并进一步影响局部质量含气率。此外混合物热物性的变化是其传热性能变化的主要因素之一，特别是在强制对流蒸发区域[4]。因此，混合物传热计算关联式的拟合和预测中，物性参数是必不可少的。纯工质的热物性参数可以通过基于实验而建立的 CSD状态方程获得，或者通过商业软件查得，例如NIST的Refprop v8.0[5]等。而对于混合物，Kedzierski等人[6]分析比较了线性、理想性和非理想性三种混合物物性关系，发现非理想性混合物物性关系最符合混合物物性变化规律。因此，本文推荐使用非理想性混合物物性关系来计算相关混合物的物性参数。下列各式为计算二元混合物推荐使用的计算公式：

各式中，下角标m表示混合物，1和2分别表示组分1和组分2，L代表液相，V代表汽相。X1代表组分1在液相中所占摩尔比例，Y2为组分2在汽相中所占摩尔比例。（2）、（3）、（4）及（5）式用于计算汽相参数时则使用汽相摩尔组分比Yl替代液相组分比。Pij为相互作用系数定义为：

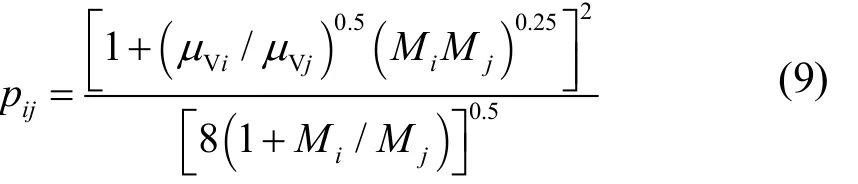
式中，Mi是纯工质组元i的分子量。

3 状态参数和质量含汽率的计算

非共沸混合物在实际的流动沸腾过程中，特别是含汽率高和质量流量大的时候，汽液相界面扰动非常剧烈，汽相流速可能远大于液相流速，流道沿程各截面处可能与理想的汽液相平衡有所偏离。此外，各处的局部流动参数存在频率较高的波动。为简化计算，本文使用的方法都基于以下假设：

a） 流道沿程各截面处都满足汽液相平衡；

b） 流动是稳定的，各流动参数和状态参数沿流动方向不存在突变；

c） 流道有很好的绝热，且对流体的加热量等于两相流体焓值的增加；

d） 不考虑过冷沸腾的影响，沸腾起始点为质量含汽率x= 0；

忽略流道流动压降，假定系统为恒压系统。在应用中，当存在显著的流动压降时，相平衡计算部分需使用局部真实压力值计算。

3.1 相平衡计算

二元混合工质的汽液相平衡判据为：

由此可得：

逸度系数φi的计算方法在此不再列出，可在相关的相平衡计算书籍中查找[7]。

由相律可知，m元混合物组成的有π个相的非均相平衡体系，其自由度F应为：

对于本文所讨论的二元两相平衡系统，系统的自由度为 2，且系统的压力为已知。因此，只需给定液相的摩尔组分比Xi，则可以计算出包括汽相组分比Yi和饱和温度Tbub在内的其它状态参数。

3.2 热焓计算

非共沸混合物流动沸腾过程中，由于组分变化导致两相混合物的蒸发温度上升，除了需要为液体汽化提供潜热以外，还需要为两相混合物提供显热，使其温度升高至新的沸点。因此，以沸腾起始点为初始值，管内流体焓值的增加包含三个部分：

第一部分为液体汽化至质量含汽率为x时的潜热，第二部分和第三部分分别为液体和气体所增加的显热。cPL和cPV使用（2）式计算获得，hLV为汽化部分的混合物潜热，是当前汽相焓值减去同压力下同组分比的液相焓值。

3.3 计算过程

二元非共沸混合物流动沸腾传热的研究需要用到汽液分相中摩尔组分比、质量含汽率和泡点温度。流体在流道中z处的局部汽液分相中摩尔组分比、质量含汽率和泡点温度可用以下具体步骤顺序进行计算。

1） 设定一个局部液相组分比估测值Xlz；

2） 使用本文3.1节“相平衡计算”所示方法计算出汽相组分比Ylz，温度Tbub-z；

3） 流经管道内两相流体总的组分比始终不变，组分1占两相混合流体总的质量分数恒定，质量含汽率xz通过求解方程获得：

公式（14）中下角标0代表沸腾起始点；

4） 使用本文3.2节“热焓计算”所示方法计算出焓值增量ΔH，并将其与实测对管道的加热量进行对比，如不相符，则重设Xlz，重复以上步骤。直至焓值增量ΔH的误差在可接受的围时，计算结束。

在实际应用中，当二元混合物的总比例一定时，在特定压力下，可以使用相平衡数据和热焓计算数据，拟合出质量含汽率x和饱和温度Tbub随焓值变化的关联式如下：

其中，H0为沸腾起始点混合物焓值，H-H0的值即为从沸腾起始点到局部点处，实际对流体的总加热量除以流道内两相流的质量流量。将以上计算方法以及获得的拟合关联式编制成计算机程序，可以进一步节省计算时间。

4 结论

1） 论述了非共沸混合工质流动沸腾过程与纯工质不同的特性，分析了混合工质沸点沿流动方向升高的原因，同时指出了相平衡计算在非共沸混合物流动沸腾传热研究中的重要性。

2） 使用相平衡和热焓计算相结合的方法研究了非共沸混合工质在流道中局部状态参数和流动参数的计算。分别讨论了相平衡计算和热焓计算的方法，详细给出了计算步骤及相关计算式，为准确获取非共沸混合工质在流道中各局部点的参数提供了一种切实可行的计算方法。

[1]Gong M Q, Wu J F, Luo E C. Performances of the mixed-gases Joule-Thomson refrigeration cycles for cooling fixed-temperature heat loads[J]. Cryogenics, 2004,44（12）∶ 847-857.

[2]刘金平, 许雄文, 张志鹏, 熊若虚, 刘雪峰. 非共沸混合工质自复叠热泵循环试验研究[J]. 低温与超导, 2006, 06∶408-413.

[3]Thome J R. Boiling of new refrigerants∶ A state-of-the-art review[J]. International Journal of Refrigeration-Revue Internationale Du Froid, 1996, 19（7）∶ 435-457.

[4]Jung D S, Mclinden M, Radermacher R, Didion D.Horizontal Flow Boiling Heat-Transfer Experiments with a Mixture of R22/R114[J]. International Journal of Heat and Mass Transfer, 1989, 32（1）∶ 131-145.

[5]Lemmon E W, Huber M L, McLinden M O. NIST Standard Reference Database 23 Version 8.0. Gaithersburg MD[D].USA∶ National Institute of Standards and Technology,2007.

[6]Kedzierski M A, Kim J H, Didion D A. Causes of the apparent heat transfer degradation for refrigerant mixtures[J]. Two-Phase Flow and Heat Transfer ASME,1992, HTD-197∶ 149-158.

[7]郭天民. 多元气-液平衡和精馏[M]. 北京∶ 石油工业出版社, 2002.

Research on the Calculation Method of Flow Boiling Parameters for Non-Azeotropic Mixtures

CHEN Gao-fei*, GONG Mao-qiong, WU Jian-feng, WANG Sheng
（Key Laboratory of Cryogenics, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing 100190）

The characteristics of non-azeotropic mixtures different from pure fluid were analyzed. Vapor-liquid equilibrium calculation and enthalpy calculation methods were used to calculate certain parameters include thermal physical properties, state parameters and flow parameters. Detailed calculating steps and related calculating correlations were presented. It provides a practical method to calculate the local parameters for non-azeotropc mixtures during flow boiling inside channels.

Non-azeotropc mixtures; Flow boiling; Two-phase flow; Vapor-Gas equilibrium calculation

*陈高飞（1983-），男，博士。研究方向：两相流与流动沸腾换热。联系地址：北京海淀中关村东路29号。联系电话：010-8254373，Email：c@mail.ipc.ac.cn。

国家自然科学基金重大项目子课题项目（No.50890183）。

本论文优选自中国制冷学会2011年学术年会论文。