抗激光散斑干扰的粒子滤波跟踪算法硬件实现

程玉宝， 蒋 斐， 倪家正

(脉冲功率激光技术国家重点实验室(电子工程学院)，合肥 230037)

0 引言

自海湾战争以来，电视制导技术一直是精确制导技术中的焦点，但是，光电对抗技术的发展对电视制导技术构成极大的威胁，尤其是激光散斑干扰［1］。目前，电视制导跟踪系统执行的跟踪算法抗干扰研究主要体现在复杂的自然背景干扰，对抗激光散斑干扰的研究较少，文献［2］基于FPGA实现的自适应卡尔曼滤波算法对背景噪声进行了处理;文献［3］基于DSP实现的相关匹配算法在自然背景下实时性良好。而对于抗干扰性较强的粒子滤波跟踪算法，目前的研究还局限于计算机仿真阶段。

本文针对粒子滤波跟踪算法计算量大、难以进行硬件实现的问题，提出了基于“DSP+ARM”技术架构的电视跟踪仿真平台。以基于达芬奇(DaVinci)技术的高集成度双核架构视频芯片TMS320DM6446(简称DM6446)为核心，设计了电视制导跟踪仿真平台，完成了粒子滤波跟踪算法的硬件实现。

1 电视跟踪仿真平台设计

电视制导跟踪平台由摄像机、视频编解码器、存储单元、图像处理单元、视频显示模块、控制单元以及伺服机构组成，如图1所示。

为了满足实时性、稳定性、智能化等性能要求，主控芯片选用了DM6446。该芯片是集成了可编程数字信号处理器(DSP)内核以及ARM处理器内核的片上系统(SoC):ARM作为主控器件，负责与外围器件通讯，协调控制数据传输;DSP进行数据处理。该方案结构灵活，通用性强，适合模块化设计，可以在不更改硬件的条件下改动相应ARM和DSP程序，从而满足不同图像源以及不同目标特性的跟踪要求;同时开发周期较短，性价比高，增强了人机交互能力，为后续平台升级和扩展提供了前提。

图1 电视跟踪平台原理框图Fig.1 The schematic diagram of TV－tracking platform

2 粒子滤波跟踪算法的硬件实现

2.1 裂变自举例子滤波跟踪算法

粒子滤波是一种基于蒙特卡罗仿真的近似贝叶斯滤波［4］，它通过非参数化的蒙特卡罗模拟实现递推贝叶斯滤波，适用于任何能用状态空间模型表示的非线性系统，精度可逼近最优估计。粒子滤波跟踪算法描述了一种鲁棒的目标跟踪框架，粒子滤波中的粒子描述目标状态的各种可能点，而滤波是滤出目标最有可能的状态。

在初始帧中，每个粒子代表目标的一个可能运动状态，包括两个参数系统状态转移时，粒子运动参数为

式中:A1、A2为常数，一般情况下取 A1=1，A2=1;B1、B2为粒子传播半径;wk－1为归一化高斯噪声量。

通过比较目标模板和参考目标的灰度分布，建立系统观测模型。取最小平均绝对差值函数为衡量相似程度的工具，即对每个粒子计算一个相似值MAD。k时刻的后验概率，就是目标跟踪中所期望的目标参数(xopt，yopt)采用加权准则表示，即各粒子根据自身权值大小决定其在后验概率中所占的比例，如式(2)所示。

至此，一次跟踪过程结束，下一时刻的跟踪仍然从系统的状态转移步骤重新开始［5］。

重采样用于解决“粒子退化”问题，淘汰小权重粒子，以权重大粒子衍生替代，并重新分配权重。裂变自举粒子滤波(Fission Bootstrap Particle Filtering，FBPF)［6］在粒子滤波跟踪算法的基础上改进了重采样过程，引入了“权值排序—裂变繁殖—权值归一”过程，简称SFN预处理过程。SFN预处理的核心是对有样本枯竭趋势的粒子集中的高权值粒子进行适当的预平滑处理。由于对高权值粒子的权值进行了重新分配，所以权值的方差减小，权值蜕化减弱，粒子集的多样性增强，避免了原先的样本枯竭问题。

2.2 基于仿真平台的粒子滤波跟踪算法实现

裂变自举粒子滤波的实现主要为系统初始化、状态转移、权重计算、权重归一化、最优估计输出和重采样6个步骤，流程如图2所示。

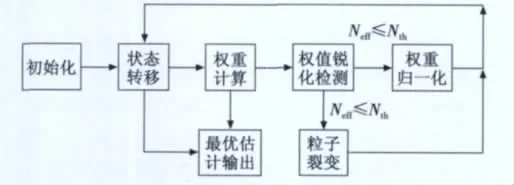
图2 改进FBPF算法流程框图Fig.2 The flow chart of the improved FBPF

在本文研究中，由于激光散斑干扰，选取灰度模板为目标描述形式，用粒子加权和来表示目标参数的估计值，粒子权值与相关值成比例。研究中选择了目标空间位置作为状态变量，这样既能满足实际跟踪需求，又能降低状态空间模型的复杂度，大大减少运算量。

设搜索区域为M1×M2(搜索量)，则计算量比值

实际编程中，O 取 0.3 ～0.5［7］。

根据先验知识，可以获得视场内目标速度V。V越大，目标在连续两帧图像间的移动范围就越大，粒子传播半径B就应越大。实验发现［7］，当2V＜B＜3V时，可以得到较好的跟踪结果。为了提高平台的抗激光散斑干扰能力，同时兼顾硬件资源和计算能力，选择B=2V。

根据系统预测方程，可以通过计算似然函数来获取粒子权重。当进行重采样后，权重被均衡化，常设为1/Ns，因此下一刻的权重及权重归一化为

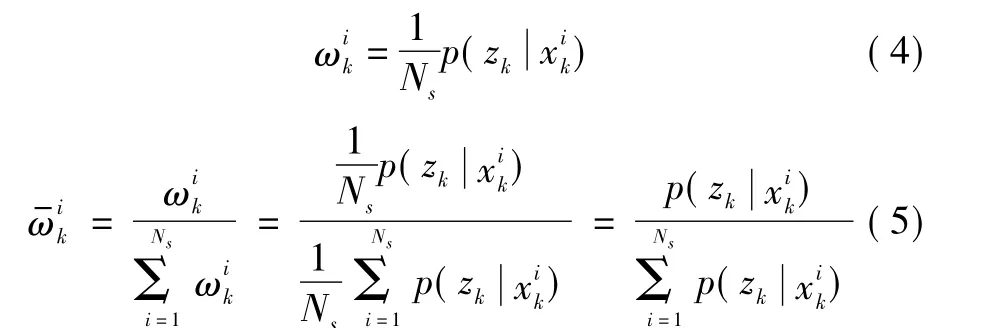
经过对FBPF算法的反复研究发现，在整个FBPF算法流程中权重归一化步骤仅仅用于计算目标最优估计和有效样本容量，而SFN预处理、重采样过程中也包含有权重归一化计算。因此在程序编写时，将权重归一化与其他步骤合并，从而减少大量除法运算，降低开销。

重采样过程主要包括权重锐化检测和SFN预处理两方面内容。

在SFN预处理判断时，权值锐化检测的有效样本容量Neff是归一化权值平方和的倒数，需要Ns+1次除法运算。因此，按照前面所述与权重归一化合并，如式(6)所示。

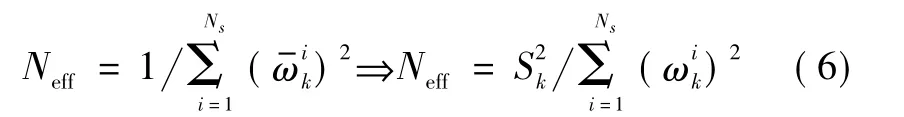
可见，整个过程仅需1次除法运算，从而省去了Ns次除法，运算量大大降低。另外，预设门限Nth的选取，一般满足Nth/Ns∈［0.3 0.8］。编程时根据实际需要折衷考虑，选用 0.6。

在权重排序过程中，粒子间依次进行权重比较，权重大的粒子存储在低地址，权重较小的存储在较高地址，同时粒子的索引值也相应交换。参照样本容量选取一定数目的高权粒子，进行裂变。根据索引值，对高地址的粒子(淘汰粒子)进行权重和状态量的覆盖。最后经权重归一化后，SFN预处理结束，进入新一轮粒子采样。

2.3 基于仿真平台的粒子滤波跟踪算法优化

2.3.1 设置编译器选项

编译器选项的设置不但控制编译的过程，还能控制程序的运行。CCS编译器中提供了若干等级和种类的自动优化选项。因此在优化时，根据实际要求，合适地选择了编译器选项，进行源程序优化，如表1所示。

表1 CCS编译器优化选项Table 1 The CCS compiler optimizing options

2.3.2 打包存储器数据

对于FBPF跟踪算法，粒子间的独立性非常适合进行打包数据操作。因此在编程时，结合DM6446的32位存储结构，采用了字对齐方式，对视频存储数据进行打包处理，便于使用内联函数进行字处理运算。具体体现在粒子MAD值计算，通过数据打包，一条指令能够处理4个像素的MAD值计算。

3 实验结果及分析

在当前实验环境下，主要测试执行性能，包括跟踪时间和跟踪精度两个方面，主要验证平台实时跟踪能力。

3.1 测试跟踪时间

实验测试时，对DSP端的粒子滤波跟踪算法中主要耗时模块进行了时间测试。在27 MHz的参考时钟下，倍频使DSP端时钟为459 MHz，ARM 端为229.5 MHz。根据实验场景，选取目标模板24*24，粒子数32，对全场视频数据Y分量进行处理。统计时，对其中一帧图像进行跟踪处理，统计粒子滤波跟踪算法以及内部主要函数的运行时间，测试结果如表2所示。

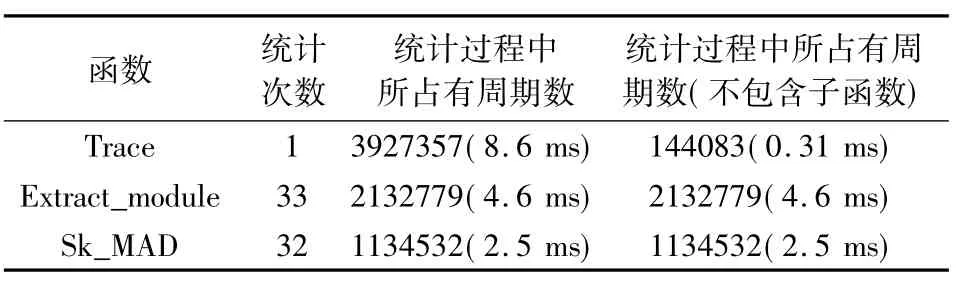
表2 粒子滤波跟踪算法执行时间统计Table 2 The implementing time of particle filter tracking

Trace函数指的是从第二帧开始运行的粒子滤波跟踪算法，该处统计的是某一次对第二帧图像进行粒子滤波跟踪算法处理所需时间;Extract_module函数用于粒子提取对应灰度区域，由于粒子数设为32，再加上初始模板提取，总共执行33次;Sk_MAD函数是指粒子进行MAD值计算，32个粒子需要进行32次MAD值计算。

通过多次执行运算统计，得出运行粒子滤波算法的平均时间为9～10 ms，远远小于帧采集时间40 ms。可以看出，改进后的粒子滤波算法在高性能仿真平台上的执行时间完全满足帧处理要求，具有良好的实时性。

3.2 测试跟踪精度

为了更好地分析硬件平台上跟踪算法的抗干扰性能，分别采用 0.095 mW、0.576 mW、1.390 mW和3.130 mW 4种不同功率的激光散斑干扰来对电视跟踪仿真平台进行跟踪精度测试。由于篇幅限制，只给出采用粒子滤波算法在1.390 mW和3.130 mW激光散斑干扰时的跟踪结果，如图3～图4所示。

图3 1.390 mW激光散斑干扰时仿真平台跟踪结果Fig.3 The simulation platform tracking result of 1.390 mW laser speckle jamming

从上面1.390 mW激光散斑干扰时的跟踪结果来看，跟踪波门自始至终都能锁定目标，保持了良好的跟踪性能。

图4 3.130 mW激光散斑干扰时仿真平台跟踪结果Fig.4 The simulation platform tracking result of 3.130 mW laser speckle jamming

当激光干扰能量为3.130 mW时，散斑很快就覆盖视场，到达近饱和状态，跟踪波门逐渐偏离目标，出现了较大偏差，但跟踪波门仍能滞留在目标周围，可见此时高权重粒子表现出了强健性。随着摄像机继续转动，散斑干扰逐渐减弱，波门将立即捕获目标。

由此可见，硬件实现的FBPF跟踪算法在整个跟踪误差测试中表现出了粒子滤波算法的“多峰”特性，使得整个仿真平台在面对激光散斑干扰时具有一定的抗干扰能力，能够准确跟踪目标。

4 结论

本文介绍了裂变自举粒子滤波跟踪算法的硬件实现，并提出了优化方案。搭建的实验仿真平台在激光散斑干扰情况下，能够充分发挥粒子滤波跟踪算法的优越性，提高了电视制导技术的实时性和精确性。相信伴随着数字信息处理技术的发展，电视制导技术的抗干扰性能将不断完善。

［1］ 陶小红，胡以华.电视制导武器激光软杀伤关键技术［J］.火力与指挥控制，2008，3(33):77－79.

［2］ 江和平，李飚，沈振康.基于FPGA实现的自适应卡尔曼滤波器的设计［J］.红外与激光工程，2005，34(1):89－92.

［3］ 李国辉，李亚安，林关成.基于多片DSP的相关匹配算法的研究与实现［J］.弹箭与制导学报，2010，30(1):58－64.

［4］ BAR－SHALOM Y，LI X R.Estimation with applications to tracking and navigation［M］.New York:John Wiley ＆Sons，2001:179－192.

［5］ 杨德贵，张长城，郑涛.粒子滤波算法的性能分析与改进［J］.电光与控制，2008，15(5):72－75.

［6］ 程水英，张剑云.裂变自举粒子滤波［J］.电子学报，2008(3):500－503.

［7］ 姚剑敏.粒子滤波跟踪方法研究［D］.长春:中国科学院长春光学精密机械与物理研究所，2004.