一种新的空空雷达主动制导导弹抗速度波门拖引干扰方法

李小龙， 王 星， 李 彬， 程嗣怡

(空军工程大学工程学院，西安 710038)

0 引言

电子战是现代空战不可缺少的作战样式。随着复合制导体制的发展，在未来空战中，具有全天候、全方位、全高度作战性能的空空雷达主动制导导弹将扮演越来越重要的角色，而该类型导弹的出现也推动了干扰技术的革新。因此，如何提高空空雷达主动制导导弹的抗干扰能力是有效发挥其作战性能的前提［1］。

在空空雷达主动制导导弹面临的干扰环境中，速度欺骗干扰技术比较成熟，是目前需要着力对付的一种干扰样式。速度欺骗干扰的主要方式有:速度波门拖引干扰，假多普勒频率干扰、多普勒频率闪烁干扰和多普勒频率噪声干扰。其中，速度波门拖引干扰是最常见的欺骗干扰技术［2］。

在速度波门拖引干扰中，干扰信号的多普勒频率相对于回波多普勒频移fd逐渐增大或逐渐减小。由于干扰幅度大于回波信号，导引头的速度跟踪电路将随干扰的多普勒频率移动而逐渐被脱离目标，最终造成目标丢失。对于频率随时间变化的接收信号，传统的一维滤波算法很难将回波和干扰分离开。

经验模态分解方法(EMD)是由美籍华人Huang N E等人提出的一种时频分析方法［3］。该方法将信号分解成不同频率成分，即固有模式函数(IMF)。高频的IMF分量一般为随机噪声，低频的IMF分量一般为原始信号。通过选择部分IMF进行信号重构，可以较好地去除高频噪声。

本文根据速度波门拖引干扰回波信号模型，采用EMD方法对回波信号进行分解。然后去掉高频分量，将余下的低频分量进行重构。仿真结果表明，该方法具有抑制速度波门拖引干扰的能力。

1 速度波门拖引干扰原理

1.1 导引头速度跟踪模型

速度跟踪的基本原理是跟踪目标的多普勒频率［4］。导弹与目标间存在接近速度所引起的多普勒效应，使得导引头所接收到的目标反射回波信号的频率与导引头发射信号的频率之间，产生一个多普勒频移，此频移与接近速度成正比。导引头速度跟踪回路就是通过对此多普勒频移的跟踪实现对弹－目接近速度的跟踪与测量。原理如图1所示。

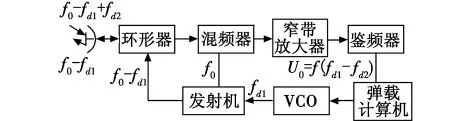
图1 速度跟踪原理Fig.1 Principle of velocity tracking

弹载计算机根据速度估值控制VCO产生的多普勒频率fd1并通过发射机调制，由天线辐射出去，由于目标存在真实速度，接收信号经混频处理后形成频差fd1－fd2，鉴频器输出频差信号到弹载计算机，由计算机调整fd1，如此循环，使频差fd1－fd2趋于零，从而完成对目标的速度跟踪。

1.2 速度波门拖引干扰机理

根据导引头速度跟踪原理，干扰机实施速度拖引时，首先转发与目标回波具有相同多普勒频率fd的干扰信号，且能量大于目标回波能量，使导引头速度跟踪电路捕获干扰信号，然后使干扰信号多普勒频率增大或减小，逐渐脱离目标回波多普勒频率，由于干扰能量大于回波，使得速度跟踪回路跟踪在干扰信号的多普勒频率上［5］。一定时间后，关闭干扰机，导引头跟踪系统由于信号消失，将被迫重新转入搜索状态。

速度波门拖引干扰的典型时序如图2所示。

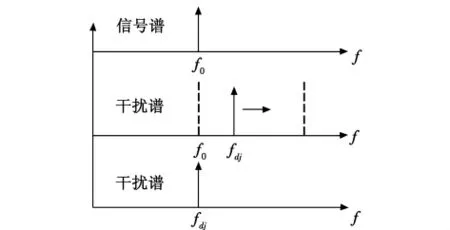
图2 速度波门拖引时序Fig.2 Time series for velocity deception jamming

干扰信号多普勒频率fdj的变化过程为

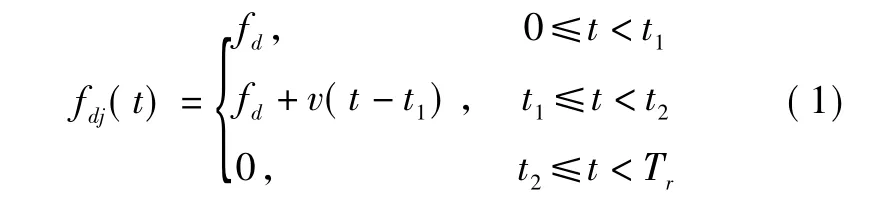
整个干扰过程可以分为3个阶段:停拖期、拖引期、关闭期。0～t1时间段为停拖期，干扰信号具有与目标回波相同的多普勒频率fd，且幅度大于目标回波，导引头末制导雷达AGC电路将根据干扰信号能量控制接收机增益，逐渐转到锁定干扰信号。t1～t2时间段为拖引期，干扰信号频率逐渐增大或减小，其变化速度不大于导引头最大识别速度。此时，跟踪电路将随干扰的多普勒频率移动，逐渐被拖离目标。t2～Tr时间段为停拖期，停止发射干扰信号，此时速度跟踪波门内既无干扰又无目标回波，导引头将重新转入搜索状态。当再次捕获目标时，开始新的拖引过程，周而复始，一次次地将速度跟踪波门拖离目标信号，使导引头找不到真信号。

2 经验模式分解原理(EMD)

Huang N E于1994年提出的EMD方法实质是对一个信号进行平稳化处理，即将信号中不同尺度的信号逐级分解，产生一系列具有不同特征尺度的数据序列［6］。通常，EMD方法分解出来的后几个IMF分量集中了原信号中主要的信息［7］，因此该部分分量一般为原始信号的趋势或均值，对混有随机噪声的信号，经分解后的高频IMF分量通常为信号的噪声。因此，EMD分解方法可以有效地进行滤波，提取原信号的趋势项。

IMF信号一般需要满足两个条件:1)从全局特性上看，极值点数必须和过零点数一致或者至多相差一个;2)在某一个局部点，极大值包络和极小值包络的算术平均值是零，即两条包络线关于t轴对称。在实际应用中只需判断待分析信号是否满足IMF信号条件即可［8］。设时间序列信号为x(t)，其上、下包络线分别为υ1(t)和υ2(t)。EMD分解的具体算法如下［9］:

1)找出原始信号x(t)的局部极大值集和局部极小值集，然后用三次样条线将所有的局部极大值点连接起来形成上包络线υ1(t)，用三次样条线将所有的局部极小值点连接起来形成下包络υ2(t)［7］;

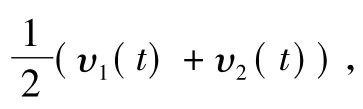
3)判断h1(t)是否满足IMF条件，若不满足，则将h1(t)作为新信号，重复以上两步，直到h1(t)满足IMF条件，记作c1(t)=h1(t)，c1(t)即为第一阶 IMF，代表原始信号的最高频分量，把c1(t)分离出来，记r1(t)=x(t)－c1(t);

4)对r1(t)作为原始信号，重复以上3步，直到rn(t)变成单调函数时，EMD分解结束。

应用EMD算法对正弦信号加高斯白噪声进行处理，其效果如图3所示。

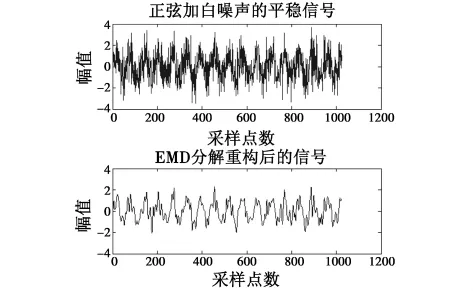
图3 加噪信号和EMD处理后的信号波形Fig.3 Waveform of signal with noise and the signal after EMD processing

由图3可看出，分解过程可理解为对信号自适应滤波过程。

3 抗速度波门拖引干扰方法

在速度波门拖引干扰中，当跟踪通道捕获干扰信号后，每接收一个照射脉冲，干扰信号频率就从目标多普勒频率值开始变化，从而使速度跟踪波门随着干扰信号移动而逐渐远离真实目标回波，达到干扰的目的［10］。对于夹杂干扰的回波信号，当分析频谱时，很难识别出真实多普勒频移，采用本文的EMD分解将初始频率值和频率增加量分离，再进行频谱分析，由多普勒滤波器截获目标多普勒频移，进而达到跟踪的目的。

设导引头发射信号为

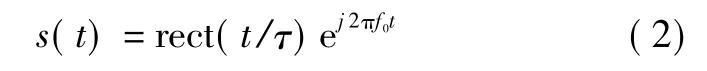
则理想状态下，回波信号为

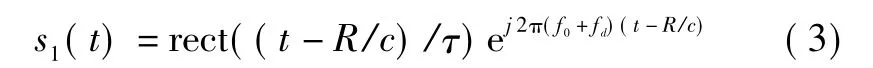
式中:fd为多普勒频移。

干扰信号可表示为

式中:A为干扰信号转发放大幅度;fdj为上文所述干扰信号多普勒频率。则，导引头接收信号为

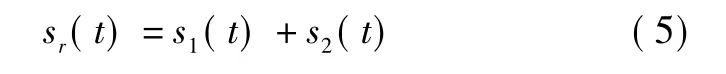
分析可知，接收信号为线性调频形式，根据EMD原理，具体处理方法如下:

1)对夹杂波门拖引干扰的多普勒回波信号sr(t)进行EMD分解，得到n个IMF分量;

2)选取后几个IMF分量进行重构，得到消除干扰后的回波信号;

3)完成重构后，当下个波门拖引干扰信号来临时，即可达到消除此类欺骗干扰的目的。

4 仿真与分析

选取一个脉冲周期进行考虑，采用典型空战参数，假设相对运动的两架战斗机，飞行速度均为800 m/s，机载雷达工作波长2 cm，则多普勒频率为1.6×105Hz。采样点数1024，波门拖引干扰调频系数10 GHz/s，干信比为20 dB。

采用EMD对回波信号进行分解重构，仿真结果如图4～图5所示。

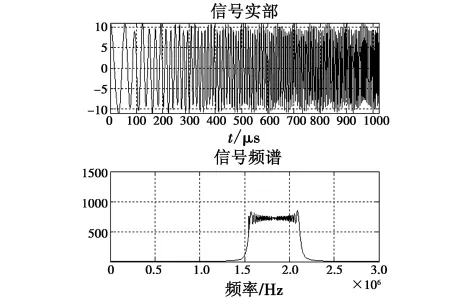
图4 被干扰的回波信号及其频谱Fig.4 The jammed echo signal and its spectrum

图5 消除干扰后的回波信号及其频谱Fig.5 The denoised echo signal and its spectrum

图4 为被波门拖引干扰的回波信号，由图可以看出干扰能量较强，干扰频谱较宽，目标多普勒频谱淹没在干扰中难以检测跟踪。

图5为采用文中方法处理后的信号，由于采用EMD分解将回波信号划分为低频分量和高频分量，重构时，忽略前几项高频分量，由图可以看出干扰基本被抑制掉。当然伴随着处理过程，回波信号有一定的失真，说明高频分量中也含有部分信号信息，更好的改进方法是对高频分量进行阈值滤波处理，但是这并不影响抗干扰的整体效果。

5 结论

未来空战电磁环境的复杂性要求空空雷达主动制导导弹必须具有较强的抗干扰能力。本文针对常用的速度波门拖引干扰，提出了基于EMD分解的抗干扰方法，通过对回波信号分解、重构，较好地抑制了拖引干扰。仿真结果证明该方法是可行的。

［1］ 张伟.机载武器［M］.北京:航空工业出版社，2008.

［2］ 赵国庆.雷达对抗原理［M］.西安:西安电子科技大学出版社，1999.

［3］ 谢启伟.经验模式分解算法分析和应用［D］.合肥:中国科学技术大学，2008.

［4］ 王国玉.雷达电子战系统数学仿真与评估［M］.北京:国防工业出版社，2004.

［5］ 王星.航空电子对抗原理［M］.北京:国防工业出版社，2008.

［6］ HUANG N E.The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis［C］//Proc.R.Soc.Lond.A，1998，454:903-995.

［7］ 杨宇，于德介，程军圣，等.基于EMD的奇异值分解技术在滚动轴承故障诊断中的应用［J］.振动与冲击，2005(2):12-15.

［8］ 谭善文.多分辨希尔伯特—黄变换方法的研究［D］.重庆:重庆大学，2001.

［9］ 陈东方，吴先良.采用EMD方法消除瞬态散射回波中的高斯白噪声干扰［J］.电子学报，2004(3):496-498.

［10］ 陈浩，何明浩，毛五星，等.小波分解在雷达抗速度欺骗干扰中的运用［J］.空军雷达学院学报，2006(1):31-33.