多无人机协同目标跟踪闭环最优控制方法
钟春梅,赵振宇,孙海波,周 锐
(1.中航工业洛阳电光设备研究所,河南 洛阳 471009;2.北京航空航天大学自动化科学与电气工程学院,北京 100083)
0 引言
远距离视线(Stand-off line of sight,SLOS)目标跟踪可保持传感器的覆盖范围,并规避目标附近的威胁区域[1-3]。文献[4]提出一种闭环最优控制方法,得到比较好的跟踪效果。但是当两架无人机(Un manned Aerial Vehicle,UAV)相互靠近或关于目标速度方向几何对称时,该方法失效。文献[1,3]提出了一种基于Lyapunov方法的闭环导引律,控制UAV跟踪地面目标,并采取盘旋策略规避目标附近危险区域(Stand-off Tracking)。但在该方法中,两架UAV必须从同一侧靠近目标,并且要求稳态时两架UAV与目标的视线差角为180°,此法不能获得最大目标估计精度。文献[5]将减小UAV控制代价、靠近目标、获得更大传感器覆盖范围和覆盖时间作为为综合指标,提高目标跟踪性能。
文献[6]基于视线夹角为90°时估计精度最优这一经验性结论,提出一种次优闭环反馈导引方法,在保证两架UAV接近目标的同时,控制两架UAV与目标之间的视线夹角趋向90°。文献[7]采取两架UAV与目标之间成90°夹角的盘旋策略来提高对地面目标跟踪的估计精度。但都是基于仿真得到的结果,均没有给出理论证明。
目前对多机协同目标被动跟踪问题研究大都采用在线优化方法,这类方法的一个突出问题就是实时性很差,或基于经验策略的方法,但又缺乏最优性证明。为此,本文提出一种由趋近和盘旋两阶段组成的多无人机协同目标跟踪闭环最优控制方法。
1 多机协同目标跟踪原理
1.1 目标跟踪系统模型
考虑两架UAV的协同目标被动跟踪问题,且不考虑高度的影响。在二维平面内,取目标的位置和速度信息为目标系统的状态向量:
假设目标做匀速直线运动,加速度方向上有过程噪声。目标模型可写成如下形式:
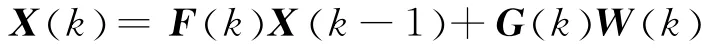
式中,X(k)为k时刻的n 维状态向量,W(k)=[w1(k) ,w2(k )]T为 零 均 值 高 斯 噪 声;F(k)和G(k)分别为状态矩阵和噪声输入矩阵。
第i架UAV对目标的方位观测方程为
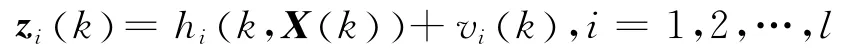
式中,l为传感器总数,zi(k)为k时刻第i个传感器的观测向量,第i个传感器的观测模型为:
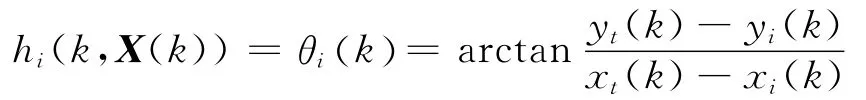
式中,( xi(k),yi(k))为第i架UAV在k时刻的位置,测量噪声vi(k)为零均值不相关的高斯白噪声,其方差为σi2(k) 。测量噪声方差阵可表示为:R(k)=diag(k),…(k))
对非线性观测模型hi(k,X(k))线性化得:
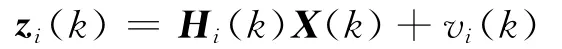
其中观测矩阵
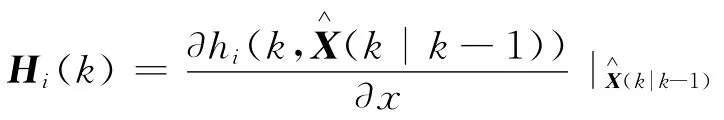
两架UAV观测方程为:
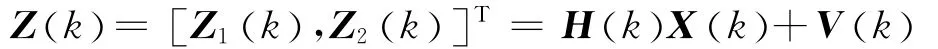
1.2 基于信息融合的目标状态估计
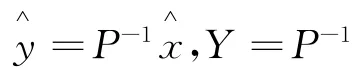
定义:
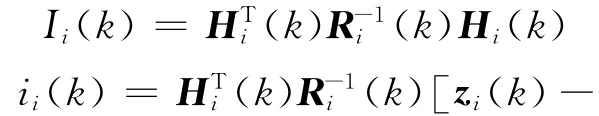

扩展信息融合估计结果为[8]:
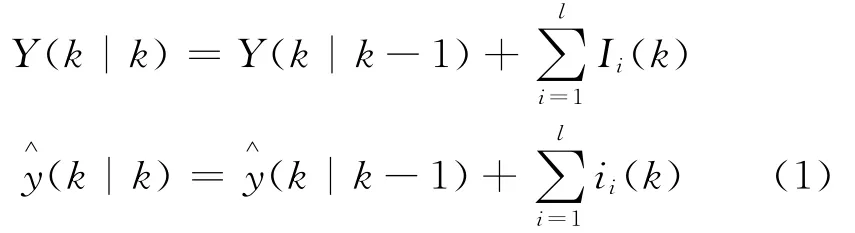
状态估计结果由下式给出:
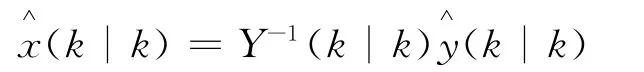
1.3 基于滚动时域优化的协同目标跟踪
为了与下一节提出的多无人机协同目标跟踪闭环最优控制方法的性能进行对比,这里给出以极小化目标状态估计方差为指标的多机协同目标跟踪滚动 时 域 优 化 (Receding Horizon Opti mization,RHO)控制方法,并考虑安全距离约束以及UAV偏航角速度约束。取RHO代价函数[9]

约束条件:
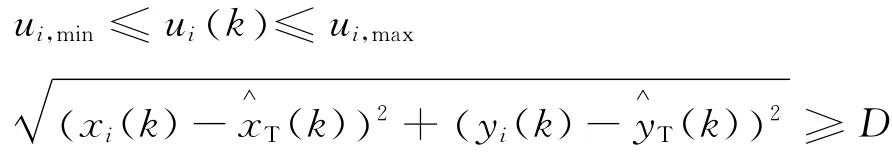
1.4 协同目标跟踪误差分析
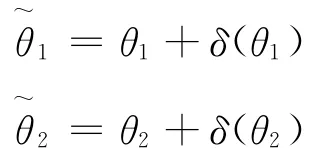
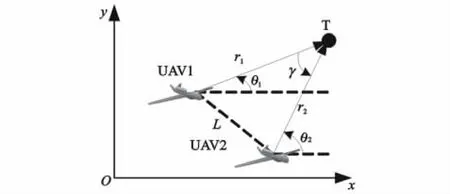
图1 双机协同目标方位观测Fig.1 Dual UAV cooperative tar get angle obser ving
UAV1和UAV2相对目标的视线夹角为
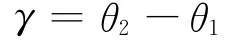
由图1可计算出目标的位置坐标

将xT和yT在真值(θ1,θ2)附近Taylor展开,并忽略2阶以上的高阶项,可得估计误差
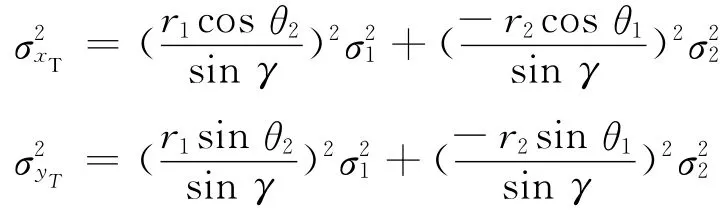
定义位置估计误差
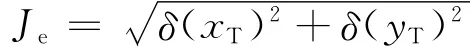
对上式求数学期望,得
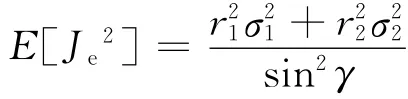
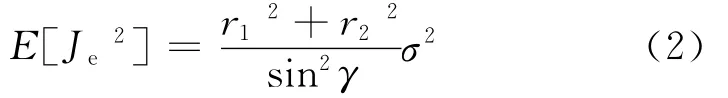
两架UAV最优观测的位置配置几何关系为:

式(2)和式(3)说明:当两架UAV尽可能靠近目标并保持π/2视线夹角时目标跟踪误差最小,这是协同目标跟踪闭环反馈控制方法提出的理论基础。
2 协同目标跟踪闭环最优控制方法
基于误差分析结论,设计闭环最优反馈控制方法,使视线夹角接近或维持90°,提高跟踪性能和实时性。将整个过程分为两个阶段:趋近阶段和盘旋阶段。
2.1 趋近阶段控制方法
针对90°视线夹角,设计UAV航向角控制[6]
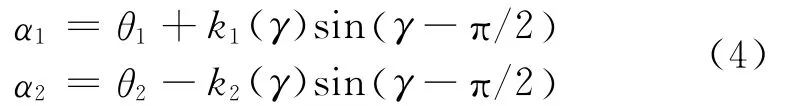
式(4)中,γ=θ2-θ1,取
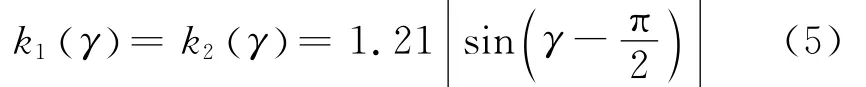
式中,θ1,θ2分量导引UAV飞向目标,缩短与目标的距离,sin(γ-π/2)分量使得两架UAV与目标之间视线夹角趋于90°,并通过比例系数k1(γ),k2(γ)调节二者趋于90°的程度。
研究发现,采用式(5)控制方法,两架UAV 在离目标距离远时分开角度比较大,靠近目标时视线夹角不够大。故提出具有距离自适应的趋近控制方法:
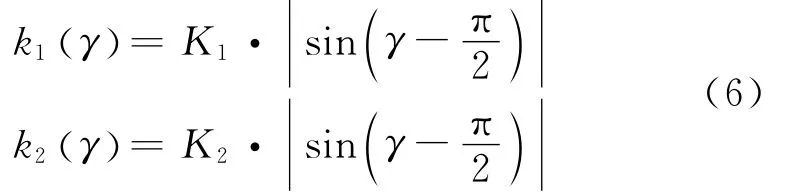
式(6)中,K1,K2为比例系数,取距离因子P,令:
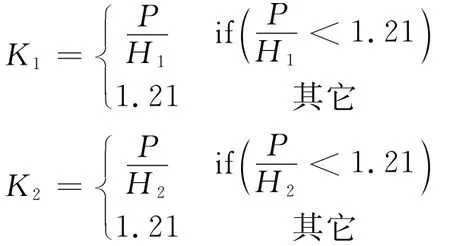
H1,H2分别为两架UAV到目标的距离。这样就实现了随距离的自适应控制:当距离远时,减小式(4)第二部分的控制量,加大UAV向目标方向运动的控制量,以趋近目标;距离近时,加大控制视线夹角的控制量,以视线更精准的测量目标。研究发现:采用式(6)控制律,UAV的跟踪轨迹与RHO方法得到的最优轨迹更加逼近。
2.2 盘旋阶段控制方法
要求UAV以一定的半径D远离目标附近的危险区域,一般是当UAV接近目标之后,围绕目标做盘旋运动。根据误差模型,最佳视角之差γ应该为90°。假设逆时针盘旋,如图2所示。保持一架UAV(UAV2)速度不变,仅调整UAV1的速度。

图2 两架UAV围绕目标盘旋示意图Fig.2 Dual UAV loitering around target
盘旋阶段控制可分为以下三个步骤。
1)盘旋时相位判定
需要判断哪架无人机处于超前位置,如图2所示,取向量(将向量扩展为三维)
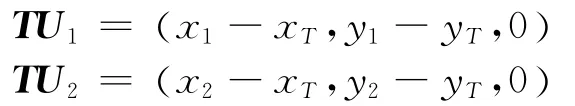
令
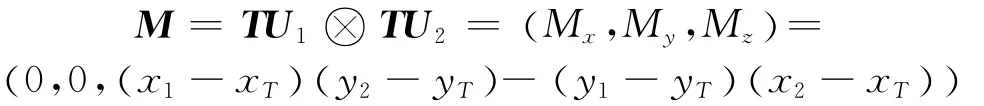
式中,符号⊗为叉乘,运算符合右手法则。如果M≥0,则说明UAV1滞后于UAV2,反之,说明UAV1超前于UAV2。
2)盘旋时航向角速率控制

其中,Vi为第i架UAV的速度,D为安全距离,也即盘旋半径。
3)盘旋时速度控制
对UAV1速度采用比例控制:
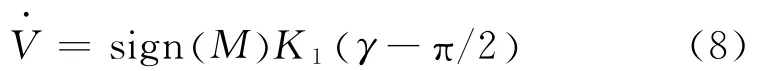
式中,sign(·)为符号函数,如果 M 为正,即sign(M )=1,说明UAV1滞后于UAV2。若γ≥π/2,即滞后角度超过π/2,此时速度控制量≥0,UAV1加速,以减小滞后角度;若γ<π/2,说明滞后角度小于π/2<0,UAV1减速以加大滞后角度。M为负数时情况与之类似。因此,通过式(8)调节UAV1的速度,使其与UAV2保持π/2的目标视角夹角。
为了防止速度调节过于频繁,设定夹角门限φ,当 γ-π/2 >φ时,采取式(8)进行调节,否则维持两架UAV速度相等做盘旋运动。
3 仿真与结果分析方法
分别采用RHO和闭环反馈控制方法对两架UAV跟踪静止和运动目标的情况进行仿真比较。设目标存在扰动,位置扰动均值(0.2 m,0.2 m),匀速直线运动时的加速度噪声为(0.2 m/s2,0.2 m/s2)。目标初始位于(2 000 m,2 000 m)处,状态初始估计为(2 100 m,2 080 m,8 m/s,8 m/s),UAV 速度为20 m/s,目标威胁半径为为300 m,UAV采样时间为1 s,仿真时间400 s。仿真结果中实线为RHO结果,虚线为闭环反馈控制方法结果。所有仿真结果中有关目标状态估计以及估计误差及方差等信息由式(1)融合得到。
情形1:两架UAV初始视线夹角近似0°
两架UAV从初始γ≈0°视线夹角位置出发,仿真结果如图3—图5所示。
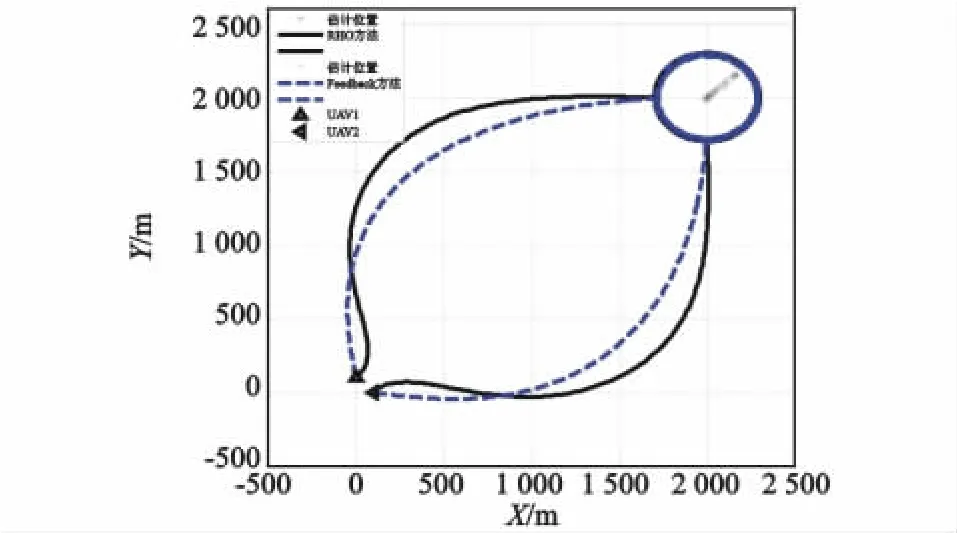
图3 情形1:UAV飞行轨迹Fig.3 Case1:UAV flight trajectory
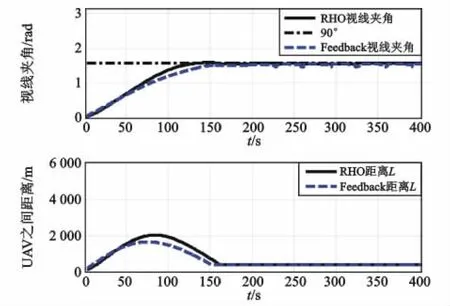
图4 情形1:视线夹角和UAV距离Fig.4 Case1:the relative distance and angle bet ween the UAVs
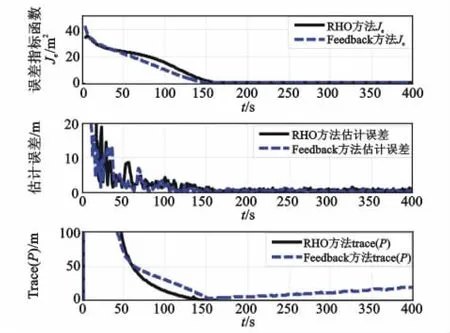
图5 情形1:误差函数、误差曲线及方差阵迹Fig.5 Case1:error f unction、error curve,and variance
由式(2)和仿真结果:跟踪时两架UAV先分开一定角度以增大sin2γ,虽然同时L增大,但此时所对应的式(2)误差函数Je和估计误差都直线下降。仿真时间150 s之后,UAV之间视线夹角γ逐渐接近90°,L趋于稳定,误差函数和估计误差也达到最小并接近稳定。
情形2:两架UAV初始视线夹角近似90°
两架UAV从初始视线夹角γ=π/2的地点出发,仿真结果如图6—图8所示。
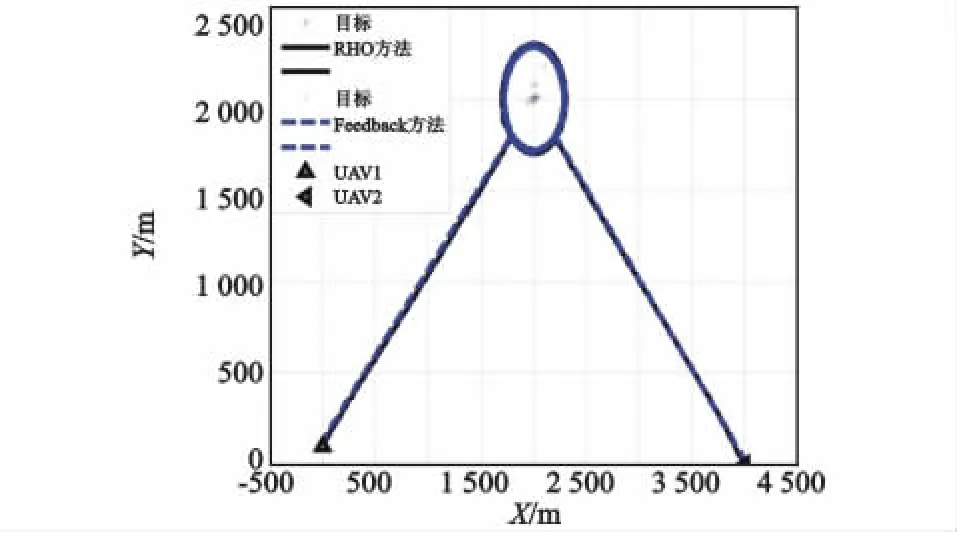
图6 情形2:UAV飞行轨迹Fig.6 Case2:UAV flight trajectory
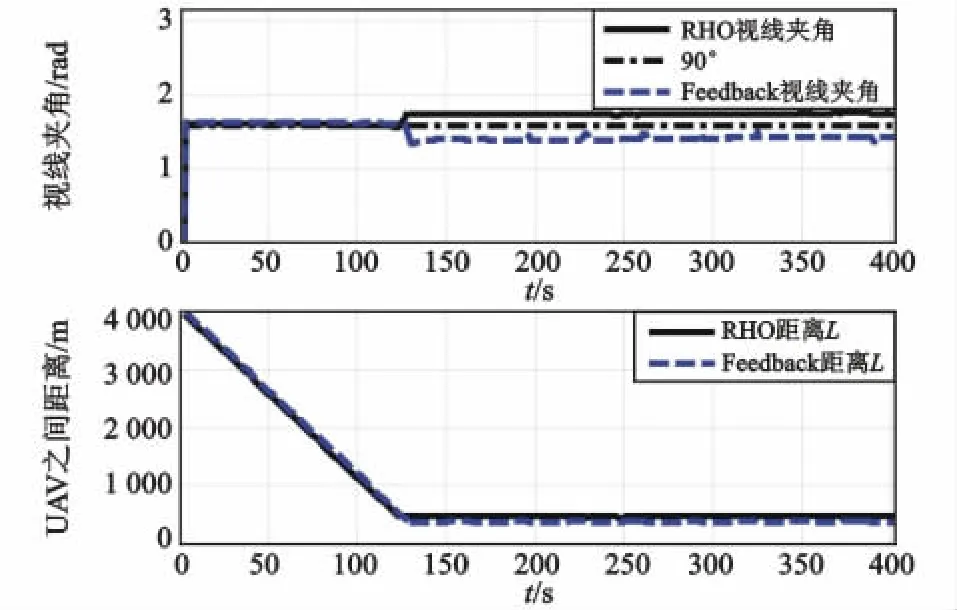
图7 情形2:视线夹角和UAV距离Fig.7 Case2:the relative distance and angle bet ween t he UAVs

图8 情形2:误差函数、误差曲线及方差阵迹Fig.8 Case2:error f unction、error curve,and variance
两架UAV几乎沿直线方向靠近目标。根据式(2),此时sin2γ已经最大,只需保持此夹角并逐渐减小。
RHO与闭环反馈控制方法的定量仿真结果对比如表1所示,闭环反馈控制方法的累积误差以及实时性要明显优于RHO。
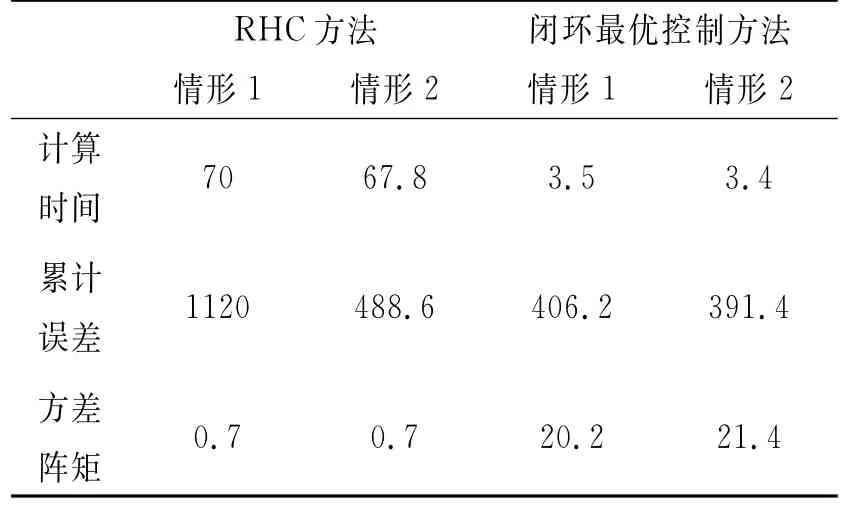
表1 RHO与闭环最优控制方法定量仿真结果对比Tab.1 si mulation results comparison bet ween the RHO and closed-loop opti mal control method
通过仿真结果可以看出:该方法具有距离自适应和角度自适应特点,在靠近阶段和盘旋阶段均确保了近90°的最优观测视线夹角,实现了协同目标跟踪闭环最优优控制,具有较好的实时性和可实现性。而且RHO和闭环反馈控制方法结果非常接近,且与式(2)误差模型结果相一致。故实际中可以直接用式(2)所示的误差函数对系统的估计误差进行评估;另外,当两架UAV初始位置接近重合或者与目标位于同一直线上时,RHO方法很容易产生滤波发散(与文献[7]现象类似),而本文方法不会出现类似现象。
4 结论
本文根据双机协同目标跟踪的最优性条件提出了一种由趋近和盘旋两阶段组成的多无人机协同目标跟踪闭环最优控制方法。该方法主要根据无人机与目标之间相对距离和方位的大小自适应调节无人机的控制量,以尽快实现最优性观测条件。仿真结果证明:该方法具有较好的最优性、实时性和可实现性。
[1]Eric W Frew,Dale A Lawrence.Cooperative stand-off tracking of moving targets by a team of autonomous aircraft[C]// AIAA Guidance,Navigation,and Contr ol Conference and Exhibit,2005(7):4 885-4 895.
[2]Rolf Rysdyk,Christopher Lu my,Juris Vagnersz.Autonomous or bit coor dination for t wo un manned aerial vehicles[C]//AIAA Guidance,Navigation,and Control Conference,2005,6:4 876-4 884.
[3]Eric W Frew,Dale A Lawrence.Steve Morris coordinated standoff tracking of moving tar gets using lyapunov guidance vector fields[C]//Journal of Guidance,Control,and Dynamics,2008,31(2):290-306.
[4]Casbeer D W,Pengcheng Zhan,Swindlehurst A L.A Nonsearch opti mal contr ol solution for a team of muavs in a reconnaissance mission[C]//2006 IEEE Inter national Conference,2006,4:IV:1 169 –1 172.
[5]Brian R Geiger,Joseph F Hor n,Anthony M DeLullo,Lyle N Long.Opti mal path planning of uavs using direct collo-cation with nonlinear programming[C]// AIAA Guidance,Navigation,and Control Conference and Exhibit.USA:AIAA,2006.
[6]Andrew J Sinclair,Richard J Prazenica,David E Jeffcoat.Opti mal and feedback path planning for cooperative attack[J].Jour nal of Guidance,Control,and Dynamics,2008,31(6):1 708-1 715.
[7]Matt Wheeler,Richard Wise,Rolf Rysdyk,William Whitacre,Mar k Campbell[C]// Autono mous Cooperative Geo-Location and Coordinated Tracking of Moving Targets,AIAA 2007 Conference and Exhibit.USA:AIAA,2007.
[8]Ben Grocholsky.Inf or mation-theroretic control of multiple sensor platfor ms[D].Sydney:University of Sydney,2002.
[9]孙海波.多无人机协同目标跟踪与打击方法研究[D].北京:北京航空航天大学,2010.

