综合优化神经网络算法*

王立威，刘琼荪

（重庆大学 数学与统计学院，重庆 401331）

BP神经网络是目前研究最为成熟、应用最为广泛的人工神经网络模型。然而，在实际应用中，如何设计网络结构、如何选取网络参数、如何提高网络收敛速度是急需解决的问题。事实上，人工神经网络模型是从输入到输出之间一个非线性映射的逼近。根据kolmogorov定理，含有一个隐层的3层BP神经网络在隐节点数足够多的情况下能以任意精度逼近有界区域上的任意连续函数[1]。由于网络参数随机性的影响，隐层神经元数的选择，至今还没有一个明确的方法。大量的实验表明，如果隐层神经元的数目偏少，网络的学习能力和处理信息的能力较差，学习误差下降缓慢，甚至出现达不到目标精度的现象；若隐层神经元数目过多，一些隐层神经元输出存在着线性相关性，就造成网络结构庞大、网络泛化能力低等问题。因此，不能完全按照kolmogorov公式或者经验公式确定隐含层神经元数目。而对于具有一定规模的、较为复杂的问题，由于其规模的不同和对求解速度的要求，更需要寻找合适的神经网络算法以确定最优隐神经元数目以保持能兼顾网络最快学习速度和良好信息处理能力的最优或较优状态。本文将多项式函数作为神经元的激活函数，结合矩阵伪逆的思想并利用区间折半搜寻的方法自动优化隐层神经元数等综合优化神经网络算法。

1 相关数学知识

1.1 魏尔斯特拉斯定理[2]

设 f（x）是[a，b]上的连续函数，则对任意给定的 ε＞0，总存在多项式 P（x），使得：

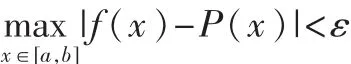
由逼近定理可知，虽然[a，b]上的连续函数是多种多样的，而多项式函数不过是连续函数类中的一种特殊类型且在连续函数类中稠密。故总可以找到一个满足定理的多项式 P（x）。

其中 wi，i=1，2，…为多项式待定系数。

在实际生活中，通常用有限项多项式 S（x）=w0+w1x+…+wnxn来代替多项式 P（x），从代数插值余项[3]的角度考虑，n 值越高，S（x）越能精确地反应连续函数 f（x）的特性。 将 S（x）作为神经元的激活函数，wi，i=1，2，…，n作为神经元输入权值，由逼近定理知，S（x）可以有效地逼近非线性映射。

1.2 权值预确定[4-6]

1.2.1 矩阵伪逆思想

由线性方程组解理论得知，线性方程组AX=b有解的充要条件是该方程组的系数矩阵的秩等于其增广矩阵的秩，即 rank（[A，b]）=rank（A）。 然而，在理论和实践中遇到的线性方程组常常无法满足同秩的条件。因此不存在常规意义上的解，但借助最小二乘法可以得到方程组的最小二乘解 X=A+b。设实矩阵 A∈Rm×n，若存在实矩阵 Xm×n满足以下 4个条件：

（1）AXA=A；（2）XAX=X；（3）（AX）T=AX；（4）（XA）T=XA则称 X为A的伪逆，即 X=A+=（ATA）-1AT。

1.2.2 权值预确定

1.3 区间折半搜寻法

此方法来源于方程 f（x）=0的根区间搜寻法，若在区间[a，b]上满足 f（a）f（b）＜0，则说明在[a，b]上至少存在一个根 x使得 f（x）=0。 取 c=，若 f（a）f（c）＜0，00则说明解区间为[a，c]，即 x0在[a，c]内，反之在[c，b]内。反复在解区间上折半搜寻方程的根，直到区间缩小到预定精度为止。

本文在优选神经元数时，首先确定最优神经元范围，然后采用区间折半搜寻法确定最优神经元数。初始隐层神经元只选取一个，以网络输出和期望输出的误差函数作为网络评价函数。在训练误差高于期望误差阶段，隐层神经元数按指数增长；在训练误差低于期望误差或者不再降低的阶段，确定最优神经元数的范围，然后采用区间折半搜寻法找出最有神经元数。

2 网络模型与算法

综合优化网络的基本思想对给定的训练样本，取网络隐层神经元数num=1，根据前述的权值预确定的方法求出初始权值，并计算网络输出、判断网络输出和期望输出的误差。若网络误差满足期望误差的要求，停止训练，网络输出权值和隐层最优神经元数num；若网络误差未达到期望误差，则将num扩大2倍，重新计算网络权值和网络误差，直到网络误差达到期望误差为止。此时，网络便确定了隐层神经元数的大致区间，在根据区间折半搜寻法，每次取区间的中点，计算网络权值和网络误差，在保证网络误差不超过期望误差的情况下确定隐层最优神经元数。

改进的网络模型：输入层到隐层间的权值默认为1，神经元激活函数为有限多项式函数 S（x），模型输出值为 S（xi）=w0+w1xi+…+wnxin，其中，n 代表隐层神经元数。综合优化网络的算法步骤如下：

（1）给定模型精度 T，门限 t（取一个很小的值），输入样本；

（2）计算权值 w和模型误差 error，确定最优隐层神经元数的范围；

（3）采用区间折半搜寻法，找出最优隐层神经元数num；

（4）输出最优神经元数num和此时网络模型的误差error和权值 w。

3 实验仿真

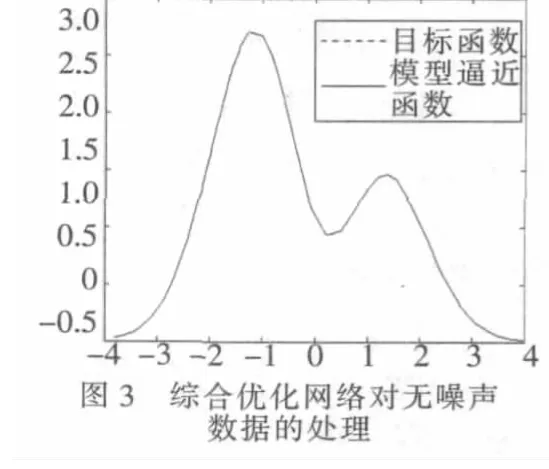
考虑 Hermit函数 f（x）=1.1（1-x+2x2）exp（-）的逼近问题。训练样本数为100，其中样本输入x～U[-4，4]。样本输出分为两组，一组为无噪声数据 f（x），另一组为有噪声数据f（x）+e，其中 e～N[0，0.1]。 产生的目标函数和噪声数据样本见图1。为了说明综合优化神经网络模型的有效性，与传统的BP模型的逼近做了对比，如表1所示。

表1 本文模型与传统的BP模型的逼近效果对比

从表中数据可以看出，对同样的样本，综合优化神经网络耗时最少，学习次数最少，收敛速度相当快，而且对非噪声数据样本处理效果非常好。尽管综合优化网络去噪能力不如BP神经网络，但不需要人为的确定隐层神经元数。简言之，综合优化神经网络可以自动优化网络结构。

综合优化神经网络和BP神经网络对Hermit函数的逼近情况见图1～图 4。

从图1～图4可知，综合优化神经网络与BP神经网络在逼近函数时优缺点不是很明显，除了在图形尖角处稍有差异外，拟合度很高。从算法角度讲，综合优化神经网络明显优于BP神经网络。综合优化神经网络不需要权值迭代，只需一步便可以计算出神经元的权值，大大减少了网络的学习时间，提高了网络的收敛速度；综合优化神经网络的参数比BP神经网络的参数少，因此受参数的随机性干扰较小。此外，综合优化网络与区间折半搜寻法良好结合，能够较好地自动优化网络结构，这也是神经网络学者一直攻克的难题之一。

根据前面的理论，基于多项式神经网络的综合优化神经网络在一元连续函数的逼近方面可以达到较好的逼近效果。但是，该网络是否适用于分类问题、多元函数的逼近问题，还需要进一步探讨。此外，该网络与区间折半搜寻法结合达到自动优化网络结构的目的在多元问题上是否仍适用也需要深层次探讨。

[1]魏海坤.神经网络结构设计的理论与方法[M].北京：国防工业出版社，2005.

[2]欧阳光中，陈传璋，朱学炎，等.数学分析（第三版）[M].北京：高等教育出版社，2007.

[3]李岳生，黄友谦.数值逼近[M].北京：人民教育出版社，1978.

[4]张雨浓，杨逸文，李巍.神经网络权值直接确定法[M].广东：中山大学出版社，2010.

[5]王建军，徐宗本.多元多项式函数的三层前向神经网络逼近方法[J].计算机学报.2009，32（12）.

[6]张雨浓，陈裕隆，姜孝华，等.一种权值直接确定及结构自适应的Chebyshev基函数神经网络 [J].计算机科学，2009，36（6）：210-213.