基于L系统的植物生长方程应用研究*
李纪永,马学强
(1.山东师范大学 信息科学与工程学院,山东 济南 250014;2.山东省分布式计算机软件新技术重点实验室,山东 济南 250014)
现代农林业对植物生长过程的研究已经越来越重视,尤其是利用计算机对植物的虚拟研究,其反映了真实的植物生长过程。虚拟植物具有操作灵活、可视性好的特点,可以在计算机上直观形象地再现植物的生长过程或者虚拟植物农场等,较好地克服了实际农林场中植物数目庞大、生理生长周期长和周围环境影响等问题。虚拟植物的生长过程可以用Lindenmayer系统 (L系统)进行植物实体的可视化建模,L系统是表达植物拓扑结构和生长规律的重要手段,是设计虚拟植物与模拟植物生长过程的重要手段之一。L系统本身可以作为虚拟植物的生长函数,并且能够结合植物的生长参数模拟植物的动态生长过程,使植物的形态发生模型与生态生理模型较好地融合。
目前,虚拟植物的研究主要是定量化地测定植物的拓扑结构,采集大量植物个体的数据,在计算机上生成植物的可视化效果[1]。但是,这忽视了植物是一个有机的整体,缺乏植物连续性生长的规律描述。因此,本文结合植物生长方程(如 Logistics方程),在 L系统中实现虚拟植物参数与植物生长特性的有机结合,并将随机L系统融合进来,真正实现植物生长过程中的某种特性(如枝干的长度)随着时间变化而发生的动态变化,体现了植物连续生长和随机生长的特点,具有重要的生物学意义。
1 L系统基本理论
L系统是由匈牙利生物学家LINDENMAYER A于1968年提出[2]的,并且作为虚拟植物生长的数学理论。L系统一般由字符集V、初始状态ω和产生式集P组成,即 L系统 G=<V,ω,P>。L系统的本质是字符串的同步并行重写,结合海龟解释[3]将L系统中的每个字符赋予特定的含义来展示植物的拓扑结构。
为了表达植物的形态特征,首先设置初始字符串和产生式集,根据产生式替换规则对原字符串进行不断的递归迭代操作。例如,初始状态ω=F,产生式P为:F→F[-F]F[+F]F。其中,海龟解释如下:
F:沿着当前的方向向前移动一步,从原先位置到当前位置画一条线段。
+:把龟形当前方向向左旋转规定的角度。
-:把龟形当前方向向右旋转规定的角度。
[:将龟形的当前状态压入堆栈。
]:从堆栈中弹出一个状态作为当前状态。
经过一次迭代后,产生式为:
F→F[-F]F[+F]F[-F[-F]F[+F]F]F[-F]F[+F]F[+F[-F]F[+F]F]F[-F]F[+F]F
迭代次数n取不同值时的植物动态生长过程如图1所示。
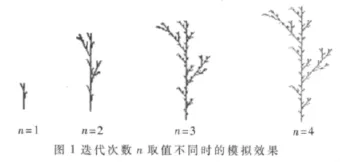
通过以上基本的L系统理论可以看出,植物的生长是一个递归、迭代的规律分裂过程,并且是有固定速率和规律的生长。因此,可以将一种植物对应一个迭代函数系统[4],通过生长方程改变其中的某些参数值来模拟植物的生长过程。
2 植物生长的曲线拟合
根据植物学基本理论,植物的生长是植物细胞按照一定的遗传规律不断发育、分裂的过程。因此,植物的生长方程可以描述为植物的生长量y(t)随时间t变化的数学模型。植物的生长过程大致呈缓慢生长、快速生长、缓慢生长和停止生长几个阶段,生长量的变化曲线大致呈“s”形。许多研究者将指数函数、双曲线函数和S-曲线函数等曲线函数应用于植物生长量的拟合,用来描述植物的生长周期、产量预测和叶片生长等。其中,大多数S-型曲线方程用于近似拟合植物节间长度和叶片尺寸等生长数据,这些曲线方程被称为植物的生长方程。
不同植物的生长过程符合不同的生长方程,对此,许多专家学者都做了不同的研究。邓红兵等[5]运用天然林中的红松、长白落叶松解析木数据[6],对树高进行了拟合和研究,结果表明,Richard方程拟合天然林中的红松最好,Mitseherlieh方程拟合长白落叶松树高比较理想。
Richards方程式如式(1)所示,Mitseherlieh方程式如式(2)所示。

其中,A为植物生长的最大高度,t为时间参数,r和c为植物生长速率参数。
Logistics方程很好地模拟了紫果云杉的树高,其生长方程为:

其中,A为植物生长的最大高度,t为时间参数,m和r为与植物生理生长有关的参数。
瑞典林学家LUNDQVIST成功地利用Korf方程建立了欧洲赤松和挪威云杉人工林的树高生长模型,其生长方程为:

其中,A为植物生长的最大值参数,t为时间参数,b和c为生长参数。
从以上学者对植物的研究可以看出,利用生长方程来拟合植物枝节长度是比较普遍的。利用生长方程从数学方法的角度对植物或植物一部分的生长数据进行系统化描述,建立植物的数学模型。通过记录植物相关数据,然后利用MATLAB软件对所要拟合的非线性生长模型定义M文件,获取公式参数,最后输出结果,从而得到非线性回归方程,即生长方程。
3 L系统植物生长形态模拟
根据植物学基本理论,在植物生长初期,植物枝节的生长速度缓慢,节间较短;在植物生长中期,生长速度明显加快,节间呈指数增长;在植物生长后期,生长速度又会变慢,最后,节间基本达到最大的长度,符合“s”形生长特点。结合L系统基本理论,可以将植物节间模拟得出的Logistics方程应用到L系统的节间长度,即海归的爬行路程,模拟植物在不同时期的生长状况。将Logistics生长方程融合到确定性L系统、参数L系统和随机L系统中,通过具体的模拟实验进行对比观察,使虚拟植物具有指导生产实际的重要意义。
3.1 D0L系统植物生长曲线拟合
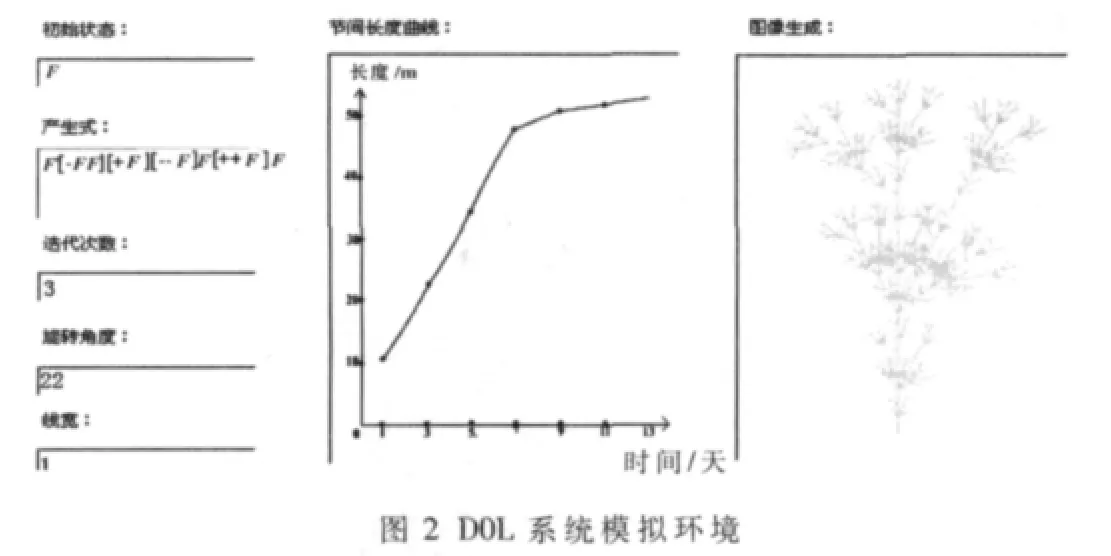
对于确定性L系统,植物生长的每一个周期都是确定性的变化,即产生式字符串周期替换,每一次的迭代可以看作是植物的周期生长。但是,根据植物学理论,植物生长的每一年龄阶段的生长速度是不同的,因此,在确定性L系统中把L系统的迭代次数表示为植物的不同生长周期,每一生长周期植物的枝干生长速度符合植物的生长规律。针对植物枝节生长的变化情况,设计模拟环境,只将Logistics生长方程应用于植物节间生长,随着时间的变化,植株节间也随Logistics生长曲线不断变化,其他的参数值均不变。设L系统的初始状态为F、产生式为 F→F[-FF][+F][--F]F[++F]F、偏转角度为 22°、线宽为 1、迭代次数为 3、节间长度以 Logistics曲线随时间的变化生长但不长新枝节时,设计环境如图2所示。
在节间长度曲线中,横轴代表时间,纵轴代表长度。植物在不同生长时期的生长状况如图3所示。
从图3可以看出,如果植物生长只是增长节间长度时,植物的总体生长量变化基本符合Logistics曲线方程的变化规律,节间生长量的变化大致呈“s”形的生长规律。
3.2 生长方程在参数L系统中的应用
参数L系统在确定性L系统的基础上增加了参数,将产生式的参数看成植物的生长周期,设置系统的初始状态以及带参数的产生式。系统中的第一次迭代表示植物起初的生长年龄阶段,即植物的第一次生长。根据生长周期与生长方程式中的时间关系,可以生成植物的初始状态。随着植物下一次生长的到来,即植物下一生长周期开始,植物不仅产生新枝而且枝节也以生长方程的曲线变化规律不断生长。例如,设L系统的初始状态为F(1)、产生式为 F(n):n<6→F(N+1)[-F(N+1)F(N+1)][+F(N+1)][--F(N+1)]F(N+1)[++F(N+1)]F(N+1)、 偏 转 角 度为 22°、线宽为 1、迭代次数 n为 4,每一次迭代代表植物的一个生长周期,与产生式的参数相关联,设定植物的生长周期与生长方程中的时间关系为2倍关系。在一次生长间隔,即植物的一个生长周期内,节间长度以Logistics生长曲线增长,生长过程以L系统产生式的生长规律迭代生长,植物的动态生长过程如图4所示。

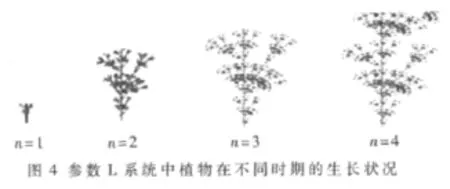
由图4可知,在模拟植物的生长过程中,节间不仅以Logistics曲线生长,并且结合参数L系统,每一次生长周期产生新枝节,符合植物随生长年龄的变化而变化的生长规律。
3.3 植物生长的随机特性模拟
不管是D0L系统还是参数L系统,生成的植物拓扑结构都是自相似性的,是有规律的生长。随机L系统的应用使植物新枝的产生并不是按照固定的拓扑结构生长,而是以随机的概率应用产生式,生成不同结构的枝干。随机L系统在参数L系统的基础上增加了参数变量π,并且增加了产生式的应用个数。当产生式字符被替代时,需要以一定的概率应用不同的产生式,这样枝节的生长具有随机性的特点。枝节的生长应用于Logistics生长方程中,使枝节的生长随着生长周期的变化而不断生长。例如,L系统的初始状态为F(1),随机L系统的产生式为:
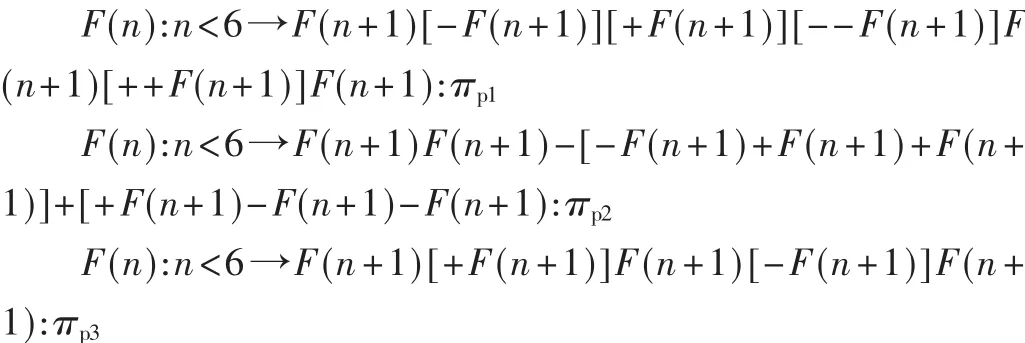
其中,产生式的应用概率分别为 πp1、πp2、πp3,取值分别为0.2、0.2和 0.6,偏转角度为 22°,线宽为 1,迭代次数为4,节间长度以Logistics方程曲线生长。这样,植物在不同生长周期的动态生长过程如图5所示。
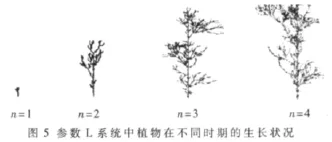
从图5可以看出,将随机L系统与参数L系统结合,并将Logistics方程应用于植物节间的生长,不仅体现了植物的随机性生长的特点,而且体现了植物的动态生长,表现出了植物的真实性和美观性。
植物模拟在计算机农业、虚拟现实等技术领域都有很好的应用。本文不仅对传统的L系统模型进行了改进,而且将生长方程应用于虚拟植物的节间生长。在L系统的改进中,尤其是融合了参数L系统和随机L系统以及生长方程的应用来模拟植物的生长。将来,生长方程将主要应用于虚拟植物模拟的以下几个方面:
(1)生长方程可以应用于基于L系统的植物各器官的模拟,体现植物的动态生长特性。不仅是植物的枝节生长,对于植物叶子的生长、果实体积的变化和植物根的长度变化和植物茎的粗细变化等,都可以根据具体的实验及结果应用植物生长方程获得生长的曲线变化。
(2)植物的生长建模不仅表现在宏观方面,也体现在微观方面。在植物的生长过程中,植物器官内生长元素数量的变化也可以应用植物生长方程的曲线变化。知道了植物的生理变化,就可以由植物的微观状态来体现植物的宏观状态变化情况。
(3)将生长方程应用于虚拟环境中,控制其中的植物动态变化情况,体现植物的美观性与真实性。
[1]ROOM P M,HANAN J S.PRUSINK IEWICA.Virtual plants:new perspectives for ecologists,pathologists and agricultural scientists[J].Trends in Plant Science,1996,1(1):33-38.
[2]LINDENMAYER A.Mathematical models for cellular interaction in development[J].Joumal of Theoretical Biology,1968(18):280-289.
[3]PRUSINKIEWICZ P,LINDENMAYER A,HANAN J.The algorithmic beauty of plants[M].Berlin:Springer-Verlag,1996.
[4]BAMSLEY M F,DEMKO S.Iterated function systems and the global construction of fractals[J].Proceedings of the Royal Socciety of London,1985,A399(1817):243-275.
[5]朱绍辉,张贵平.Richards生长函数在意大利杨树无性系人工林生长预测上的应用[J].江苏林业科技,2000,27(1):27-30.
[6]邓红兵,王庆礼.红松、长白落叶松树高生长模型的研究及应用[J].辽宁林业科技,1997(5):24-27.

