减小塔影效应载荷波动的独立变桨距控制研究

陈 雷 孙宏利 邢作霞

（沈阳工业大学风能技术研究所，沈阳 110023）

近年来，风能作为可再生清洁能源，得到了快水速的发展。海上风速大且稳定，利用小时数可达到3000h以上。同容量装机，海上虽比陆上成本增加60%，但电量却增加50%以上。因此，海上风电机组是未来风电产业发展的新领域、新潮流。

平轴风力机根据来流、叶片、塔架的相对位置，可分为上风向风力机和下风向风力机。海上风速大，引起的叶片形变也大，对于上风向风力机来说，当叶片经过塔架所在位置时，容易与塔架发生碰撞，造成风电机组的损坏，因此，下风向风力机是海上风电机组发展的趋势。下风向风力机由于塔架在扫略面的前方，受到的塔影效应影响更大些。

目前，主流兆瓦级以上的三桨叶水平轴风电机组，其直径接近或超过百米，同时叶片空间互差120°。由于塔影效应影响，加剧了叶片在风轮扫略面上所受到的空气动力载荷的周期型变化，同时对风电机组的输出功率也会产生一定的波动[1-2]。降低载荷波动的比较有效且可行的办法就是使用独立变桨距调节技术，给每个叶片叠加一个独立的桨距信号，使3只叶片具有不同的空气动力学特性，以补偿风的不均匀性引起的俯仰载荷和偏航载荷[3-9]。

本文对独立变桨距控制系统引入坐标变换-Coleman变换，将风轮线性时变模型变换为线性时不变模型，同时将系统部分解耦，简化控制器的设计。在此基础上，建立独立变桨距控制系统，对风电机组的载荷情况进行仿真研究，并与采用统一变桨距控制策略的风电机组进行比较分析。

1 塔影效应

塔影效应是指由于塔架的阻塞作用引起的塔架后面的风速降低的现象。根据定义来看，似乎塔架只是对下风向风力机有影响。其实在上风向条件下，塔架-转子的相互作用与扫略面和塔架之间的距离有密切关系。只有转子在塔架上游的很远处时，塔架-转子的相互作用才可以忽略。而在下风向条件下，转子在塔架的下游。每当转子扫过塔架的时候，都会与塔架后面一个风速降低区域内的湍流产生相互作用，这个区域就被称为塔架尾迹区或塔影区。因此，对下风向风力机而言，塔影效应问题更突出一些。

风轮旋转时，桨叶在风轮扫掠面中的位置呈周期性变化，在经过塔架所在位置时，由于塔影效应的影响，会加剧叶片在风轮扫掠面上所受到的空气动力载荷的周期性变化。而周期性气动载荷会引起叶片动响应，响应又反馈于外部气动载荷，使得本就复杂的风力机振动、疲劳等问题变得更加复杂且不容忽视。同时由于载荷的周期变化，对并网的风电机组来说，其输出功率也存在一定的波动，输出电能质量会受到一定影响。

塔影效应主要有三种不同的模型：上风向的潜流模型、下风向的经验塔架尾迹模型和组合模型。

1.1 潜流模型

这个模型适合于运行在塔架上风向的风轮。塔架上风向的纵向风速分量(V0)用一个假设来修正，该假设认为在一个直径为 D=FDT的圆柱状周围层流是不可压缩的，这里DT是要计算塔影的高度处的塔架直径，而F是塔架直径修正因子。对于塔中心线前方距离为 z，穿过该中心线的风向量的边相距为x的一点来说，风速V由下式给出

其中

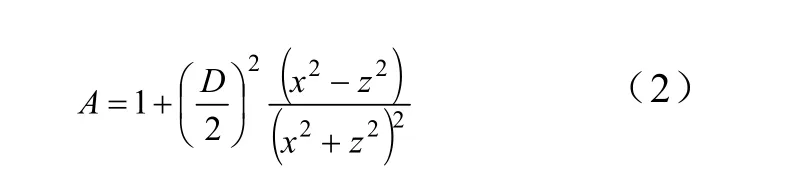
1.2 经验模型

对于运行在塔架下风向的风轮，提供了经验模型。对于塔中心线前方距离为 z，穿过该中心线的风向量的边相距为x的一点来说，风速V由下式给出

其中

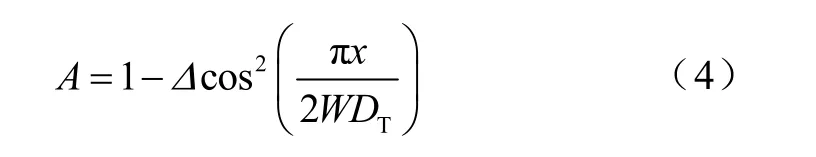
适合于底部正中心线±60°范围内的方位角。关于其它方位角，应用潜流模型中的修正方式。这里Δ是作为局部风速的一部分在尾迹中心处的最大速度差，而W是作为局部塔架直径DT一部分的塔影高度。对给定的下风向距离，这些量被定义，也可由DT表达。对于其它的距离，W增大，Δ将随距离的平方根减小。

1.3 组合模型

组合模型只是在塔的前部和侧边应用潜流模型，而在下风点处无论用其它哪一个模型均有较大的不足。为了确保平稳过渡，在任何小区域内使用两个模型的A因子积，在这些小区域内由潜流模型给出加速流，而由经验式模型给出速度差。

2 风轮模型

2.1 风轮空气动力学线性时变模型

风轮具有非线性的空气动力学特性，而非线性控制理论目前仍不成熟，应用非常困难。因此，为了利用发展成熟的线性控制系统理论，以便于控制器的设计，首先要得到风轮的线性化模型[10]。

对于三叶片风机而言，风轮转动惯量为 J，风轮角速度为Ω，主轴转矩为Mrotor，塔架上顶部质量为M，塔架前后位移为snod，塔架左右位移为snay，轴向力为Fax，轮毂高度为H，塔架刚度为S，塔架阻尼系数为D，俯仰弯矩为Mtilt，侧向力为Fsd，偏航弯矩为Myaw。

风轮旋转和机舱的运动方程为

式（6）和式（7）中的输入变量{θi∣i=1,2,3}和{ui∣i=1,2,3}分别为 3个叶片给定桨距角变化量和各叶片上的有效风速变化量。变量{ψi∣i=1,2,3}是风轮叶片的方位角，由式（8）给出

kMx,、hMx分别为气动转矩对桨距角、气动转矩对风速的导数；

kFx,、hFx分别为叶片挥舞力对桨距角、叶片挥舞力对风速的导数；

kMz,、hMz分别为叶片挥舞弯矩对桨距角、叶片挥舞弯矩对风速的导数。

从风轮的运动方程及俯仰弯矩和侧向力的表达式可看出，俯仰弯矩和侧向力受到多个变量的影响，且相互之间有强耦合，控制器的设计将十分复杂。为简化计算，便于利用强有力的数学工具，将风轮的运动方程写成状态空间描述。由于变量之间的耦合，直接按照多变量时变系统设计控制器会遇到众多困难，且效果很难达到要求。为了简化控制器的设计，引入坐标变换-Coleman变换，将线性时变系统模型变换为线性时不变模型，变换后的变量加上标cm以示区分。令Coleman变换矩阵为P，则有

2.2 风轮线性时不变模型

经过Coleman变换后，得到的风机线性时不变模型如式（10）和式（11）所示。

由式（10）和式（11）可以看到，方程系数矩阵已不含有时变系数，且出现了众多0元素，将系统部分解耦，这大大简化了控制器的设计。

3 独立变桨距控制系统

式（10）和式（11）已给出风轮线性时不变模型，在此基础上，建立独立变桨距控制系统，原理图如图1所示。

在系统原理图中，u1、u2、u3是 3 个叶片上的风速，通过P-1（Coleman逆变换）转换为Coleman坐标系下叶片上的风速、、，其作为线性时不变风机模型的输入。、、是Coleman坐标系下的3个叶片的桨矩角，也是模型的输入。Ω是风轮转速，输入到PID控制器，可得到叶片1的桨矩角。、、是Coleman坐标系下的3个叶片的叶片弯矩，其中、输入到PID控制器，可得到其他两个叶片的桨矩角。风力发电机各叶片根据各自得到的桨矩角进行变桨距操作。

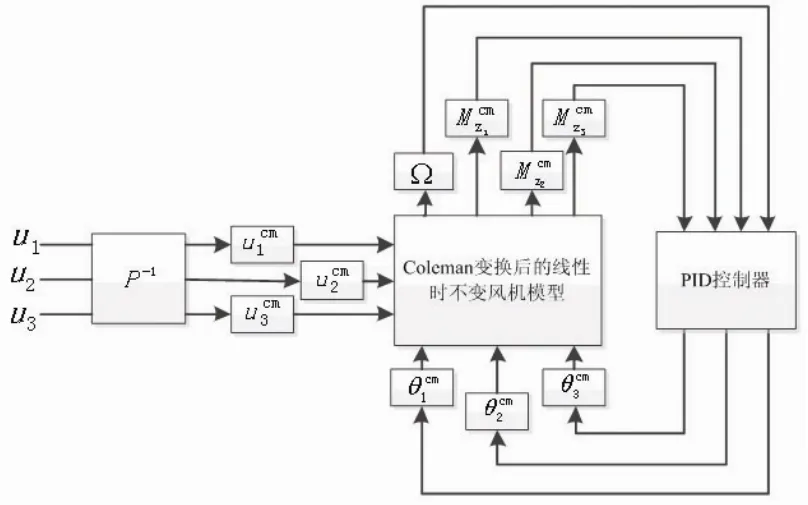
图1 独立变桨距控制系统

系统中的独立变桨距控制器和功率控制器采用的是 PID控制，具有算法简单、鲁棒性好和可靠性高等优点，广泛应用于工业自动控制领域。由于风轮模型经过 Coleman变换变换为线性时不变，所以采用PID控制可以简化控制器设计，并达到设计要求。

4 仿真结果

利用 Bladed软件对控制系统模型进行仿真研究。以叶片有效风为输入信号，对风电机组在塔影效应影响下的如下两种情况进行仿真对比。

情形 1：统一变桨距控制（collective pitch control，CPC）；

情形 2：独立变桨距控制（individual pitch control，IPC）。

该模型参数取自 3.0MW风力发电机(以下简称风机)。参数的测定是在湍流强度为 0.14，风速为14m/s，风轮速度为14.31r/min的情况下进行的。当考虑塔影效应时，塔架直径修正系数是1。

3MW风机的气动载荷系数如表1所示。

表1 3MW风机的气动载荷系数

仿真中所用的风信号如图2所示。

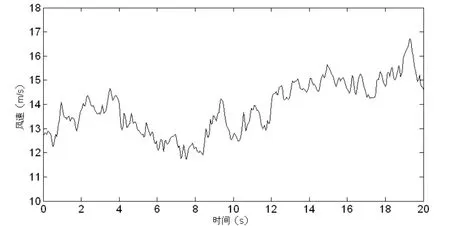
图2 3个叶片上的平均风速

图3和图4分别为考虑塔影效应影响时，风轮中心的俯仰弯矩和偏航弯矩的时域仿真结果。

图3 考虑塔影效应影响时，统一变桨距与独立变桨距风轮中心俯仰弯矩对比曲线

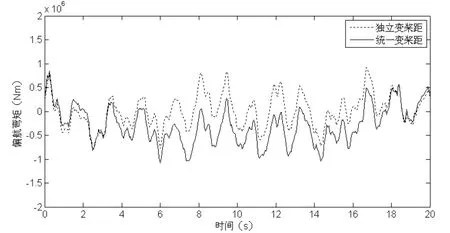
图4 考虑塔影效应影响时，统一变桨距与独立变桨距风轮中心偏航弯矩对比曲线

从图3和图4可看出，对于塔影效应影响，统一变桨距控制俯仰弯矩和偏航弯矩的波动较剧烈；独立变桨距控制俯仰弯矩和偏航弯矩幅值较统一变桨距而言波动情况得到了改善，也就是说，独立变桨距系统减弱了载荷的波动性。

图5是通过雨流统计方法得到的，统一和独立变桨距控制20年的疲劳载荷对比曲线。该曲线共有128节台阶，即将整个风机在 20年寿命当中的疲劳载荷分成128段，判断每次交变属于哪一段，就给对应的段加 1，把所有工况都统计完后，就得到了阶梯型的曲线。曲线下方的面积越大，说明风机所受的疲劳载荷就越大，也就是说风机的疲劳损伤就越大。从图5可看出，采用独立变桨距控制策略的风机所受的疲劳损伤远小于统一变桨距，得到了很大的改善。

图5 在风机20年寿命当中，统一变桨距控制与独立变桨距控制疲劳载荷对比曲线

5 结论

对两种变桨距控制方法进行对比研究：即统一变桨距控制和独立变桨距控制。仿真结果表明，对于塔影效应的影响，独立变桨距控制较统一变桨距而言显著地减弱了载荷的波动情况，并且采用独立变桨距控制策略的风机所受的疲劳损伤要远小于采用统一变桨距控制策略的风机，延长了风机的使用寿命。

[1]孔屹刚,顾浩,王杰等.基于风剪切和塔影效应的大型风力机载荷分析与功率控制[J].东南大学学报,2010(40): 228-233.

[2]张弘鲲,孟祥星.塔影效应引起的风电机组输出功率波动问题[J].东北电力技术,2011(4):33-35.

[3]叶杭冶,李伟,林勇刚等.基于半物理仿真的变速恒频独立变桨距控制[J].机床与液压,2009,37(1):90-93.

[4]林勇刚,李伟,陈晓波等.大型风力发电机组独立桨叶控制系统[J].太阳能学报,2005,26(6):780-786.

[5]M.Maureen Hand, Mark J.Balas. Blade Load Mitigation Control Design for a Wind Turbine Operating in the Path of Vortices[J].Wind Energy, 2007(10):339-355.

[6]Peeringa, J.M. Comparison of extreme load extrapolations using measured and calculated loads of a MW wind turbine[C]. Gepresenteerdop European Wind Energy Conference 2009, Marseille, France, 2009:16-19.

[7]Holierhoek, J.G, Braam, H. Determination of load cases and critical design variables[R]. ECN wind energy,2010(2).

[8]孔屹刚,王杰,顾浩等.基于风剪切和塔影效应的大型风力机独立变桨距控制研究[J].华东电力,2011,39(4): 640-644.

[9]胡岩,刘玥,姚兴佳等.兆瓦级风力发电机组多段权系数独立变桨距控制[J].沈阳工业大学学报,2009,31(6):633-638.

[10]T.G. van Engelen. Design model and load reduc- tion assessment for multi-rotational mode indi- vidual pitch control[R]. European Wind Energy Conference &Exhibition,Athens, Greece, 2006.5.