基于自适应人工鱼群算法的输电网网架规划
钟 蔚 李天友
(1.福州大学电气工程与自动化学院,福州 350108;2.福建省电力有限公司,福州 350002)
输电网网架规划是指220kV及以上电压等级的网架规划,其主要任务是根据电力系统的负荷预测和电源发展状况对输电网的网架做出发展规划[1]。
输电网网架规划是一种非线性组合优化问题,并带有大量复杂的约束条件。输电网网架规划的主要方法有数学优化方法和启发式方法两类。其中数学优化方法虽然可以准确找到最优方案,但是对于复杂网络计算量过大。启发式方法是基于系统某一性能指标对可行路径上参数做灵敏度分析,并根据一定原则选择要架设的线路[3]。近年来应用于输电网网架规划的启发式方法主要有:遗传算法(GA)、蚁群算法(ACA)、粒子群算法(PSO)、模拟退火法(SA)等。虽然启发式算法计算量小,但对于如何解决搜索能力和效率之间的矛盾,以及如何提高克服局部极值的能力上还有待于进一步研究[3]。
人工鱼群算法是浙江大学的李晓磊博士于 2002年提出的仿生智能算法,是行为主义人工智能的应用。它从构造单条人工鱼的底层行为做起,从单条人工鱼的局部寻优开始,最终使得全局最优值在鱼群中突现出来,该算法具有良好的全局收敛能力,并且对初值的依赖程度很小,是基于鱼群的集群行为进行寻优的算法,属于群智能算法的范畴[3]。本文对于人工鱼群算法容易陷入局部极值而导致收敛速度慢的问题,针对觅食视野进行自适应的调整,改善算法后期收敛速度,提出了适用于输电网网架规划的自适应人工鱼群算法,并通过6节点算例和18节点验证了算法的有用性和优越性。
1 算法介绍
1.1 人工鱼群基本步骤
人工鱼群算法的特点是对初值的要求不高,不需要了解问题的特殊性,有较快的收敛速度。以求目标函数极小值为例,基本人工鱼群算法步骤如下:
1)觅食:假设一条人工鱼当前位置为Xi(一条人工鱼代表一种规划方案),在视野visual内随机选择一个新位置Xj,若iY>Yj,说明新位置的浓度更优,向该位置前进一步;否则重新随机选择位置进行判断;反复尝试Trytime次后,若仍不满足前进条件,则随机移动一步。
2)追尾:假设人工鱼当前位置为Xi,搜索当前视野内的伙伴中目标函数最优的伙伴位置Ymin,如果Yi<Ymin,且视野内伙伴数t满足t/N<δ,其中:N为鱼群总数;δ为拥挤度,0<δ<1。表明该处食物浓度高且不太拥挤,立刻移动到该伙伴处。
3)聚群:假设人工鱼当前位置为Xi,在视野内搜索伙伴数目t并确定中心位置center,若满足t/N<δ,且 Ycenter<Yi,则表明中心位置的食物浓度高且不太拥挤,可以向中心位置移动,否则随机移动一步。
在算法中设置一个公告板,记录最优人工鱼个体的位置ggbx以及该人工鱼位置的食物浓度ggb。每条鱼在进行一次行为后就将当前状态和公告板进行比较,如果优于公告板则用自身状态替代公告板。
1.2 算法的改进
视野对算法中各行为影响是比较复杂的。当视野范围较小时,人工鱼群的觅食行为和随机游动比较突出;视野范围较大时,人工鱼的追尾行为和聚群行为将变得较突出。总体来看,视野越大,越容易使人工鱼发现全局极值并收敛。因此对人工鱼的视野进行适当的改进,是提高人工鱼群算法优化性能的一种方法。
在基本的鱼群觅食过程中,当迭代次数增加时,人工鱼群越来越逼近最优解,此时人工鱼的决策变量中可能仅仅有一两个变量异于最优解。此时,若按照原先的觅食视野进行搜索,很可能错过最优解,进行无谓的搜索,造成尝试次数trytime很大,增加了计算时间性,甚至于影响最终的寻优结果。可见,收敛速度和最后寻优结果都很大程度上基于视野的大小。因此,提出如下改进策略:
在鱼群算法的觅食初始阶段,每条人工鱼以一个较大的视野寻优。随着迭代次数的增加,鱼群的视野范围将适当的减小以增加收敛精度同时加快收敛速度。第k次迭代中觅食视野的计算式为
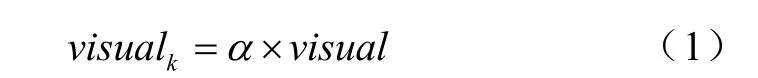
其中,α是衰减因子,且0<α<1。意味着随着迭代的进行,视野相应的变小。α的取值根据当前人工鱼和上一代最优人工鱼(当前公告板对应的个体)的距离来确定,在网架规划问题中距离表示如下

其中,Xi为当前人工鱼的位置、X为上一代最优人工鱼的位置;xor和sum为Matlab中的异或函数,用于计算两个决策变量中不同元素的个数,即网架规划问题中不同方案中线路连接的差异。
2 输电网网架规划数学模型和自适应人工鱼群算法流程
2.1 输电网网架规划数学模型
1)经济型数学模型
经济型数学模型的目标函数包括线路新建和运行费用两部分。其中,认为线路的投资费用只与新建线路的长度和运行费用有关,因此考虑一次性建设费用和年网损费用。得到的目标函数为
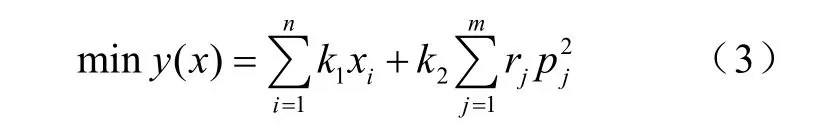
其中,miny(x)年投资费用,包括线路建设费用和线路运行费用(万元);xi0-1决策变量,代表第i条线路建设与否;k1支路 i中新建一回线路的建设费用(万元);k2年网损费用系数;rj支路 j的电阻(Ω); pj支路 j正常运行时输送的有功功率(MW);n新建线路条数;m网络中线路总条数。
约束条件为

其中,B网络节点导纳矩阵;BL支路导纳对角阵;A网络节点关联矩阵;PG发电厂功率向量(MW);PL负荷功率向量(MW);θ节点电压相角列向量;ximax支路i可扩建线路回路数。
上述模型第1项是新建线路建设费用,第2项是线路运行费用,由于输电线路电阻值相对电抗值较小,通常可以略去线路运行费用。
2)“N-1”安全数学模型
“N-1”安全数学模型是建立在经济型数学模型之上,采用相同的目标函数,同时在经济型数学模型的约束条件上加入“N-1”下的网络潮流约束条件,潮流计算同样采用直流潮流计算方法。增加的约束条件如下:

其中, B'网络中断开某条线路后的节点导纳矩阵;网络中断开某条线路后的支路导纳对角阵;θ'网络中断开某条线路后的节点电压相角列向量。
“N-1”安全数学模型即在满足正常运行时线路过负荷校验时,还需进行系统断线分析。即断开系统中的一条线路,判断系统中其他线路是否过负荷,若线路过负荷则该方案淘汰;若各线路均为过负荷,则重新合上断开的线路,随机断开另一条线路进行判断,如此反复,直到随机断开系统中任意一条线路其他线路均不过负荷则该方案满足“N-1”。在断开线路进行潮流计算时,还需判断系统是否解列,如为解列再进行下面的过负荷判断。
2.2 应用于输电网网架规划的自适应人工鱼群算法流程
1)设置人工鱼种群数N,最大迭代次数Gmax,视野visual,觅食尝试次数trytime,拥挤度δ等等,输入网络结构参数。
2)初始化人工鱼群,使初始化的人工鱼群满足连通性和潮流约束条件,计算每条人工鱼的食物浓度,令食物浓度最小者进入公告板中。
3)各人工鱼在满足约束条件下分别执行觅食、追尾、聚群行为尝试,然后取食物浓度最低的行为实际执行,缺省行为为静止不动。
4)各人工鱼行动一次后和公告板的食物浓度进行比较,若优于公告板的食物浓度则取而代之,同时在下一次迭代的觅食行为开始前判断是否改变视野。
5)判断是否达到最大迭代次数,若是则迭代结束输出最优结果至公告板,否则转第2步。
3 算例分析
算例1采用6节点系统进行算法可用性测试[4],规划前的网络结构如图 1。电源、负荷、线路参数及网络结构见文献[5]。算例原有输电线路6条,新增1个电源节点,可扩建线路有22条。线路投资费用为 20×104元/km,规划前网络结果如图 1所示。在Matlab环境下进行基本人工鱼群算法和自适应人工鱼群算法编程,鱼群种群数 N取 20;初始视野visual取5;觅食最大尝试次数trytime取20;最大迭代次数Gmax取50;拥挤度δ取0.4。得到经济型数学模型的最优规划图如图2所示。
该网架规划结果和文献[5]的规划结果一致,证明了本文算法的有用性。图3是人工鱼群算法的一次测试曲线对比图。图中横坐标代表迭代次数,纵坐标代表年费用值(万元)。实线代表基本的人工鱼群算法收敛曲线,虚线代表自适应人工鱼群算法收敛曲线。

图1 规划前网络

图2 规划结果

图3 算法收敛曲线对比图
由图3可见,在某次测试过程中,实线代表的基本人工鱼群算法没有收敛至最优解 4000万元,而收敛至次优解 4620万元,这是由于基本的人工鱼群算法的视野visual是固定不变的,在迭代的初期,由于视野较大,收敛的速度较快,但在收敛后期接近极值点时由于视野visual太大而收敛速度缓慢且容易错过极值点,无法跳去局部极值(次优解)。据此,自适应人工鱼群算法据此对视野 visual进行了动态的调整,即根据当前人工鱼和上一次迭代的最优人工鱼的距离来改变当前迭代的视野visual大小。且对电网规划而言,当方案接近或者达到局部极值点时想要突破局部极值而到达全局极值往往需要对方案至少进行“成对变异”,即在删去一条线路的同时需要增加一条更合理的线路。因此,本文设置了自适应人工鱼群算法在迭代后期的视野visual为偶数。
由表1可见,在50次试验中,自适应人工鱼群算法均能收敛至最优解,而基本人工鱼群算法和文献[6]的遗传算法SGA均不能全部收敛至最优解;此外,在收敛至最优解的迭代次数和迭代时间上,自适应人工鱼群算法均优于另外两种算法。可见,自适应人工鱼群算法具有较高的搜索效率和收敛速度。

表1 性能比较
算例2采用18节点系统进行算法灵敏度和优越性测试,18节点系统原有10个节点,9条支路,在未来规划年,系统增加为18个节点、27条线路。系统的初始网络结构见图 4,初始参数见文献[5]。线路投资单价取 100×104元/km。在 Matlab环境下进行自适应人工鱼群算法编程,鱼群种群数N取30;初始视野visual取5;觅食最大尝试次数trytime取20;最大迭代次数Gmax取30;拥挤度δ取0.35。得到经济型数学模型的规划图如图5所示。

图4 18节点系统网络初始结构图

图5 经济型数学模型规划图
采用文献[2]的改进 PSO 算法和文献[5]的IAFSA算法和本例的自适应人工鱼群算法结果进行比较,为了便于比较,把文献中网架投资的单价均折算为10×104元/km。结果如表2所示。

表2 三种算法比较
由表2可知,本文采用的自适应人工鱼群算法得到的年费用要低于另外两种算法,表明了算法的优越性。图6是该算例满足“N-1”约束的18节点系统网架规划图。
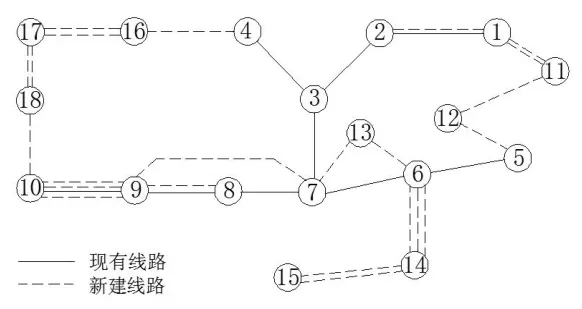
图6 “N-1”安全模型网架规划结果图
由图6可见,该规划结果是在经济型数学模型的网架规划图上增加了 10条线路,年总费用为263600万元。表明自适应人工鱼群算法在规划满足“N-1”安全约束的网架模型中也是适用的。
4 结论
本文针对输电网网架规划问题提出了自适应人工鱼群算法,对觅食视野建立了反馈机制,较之基本的人工鱼群算法可以有效避免人工鱼群算法陷入局部最优点,兼顾了全局和局部搜索能力。通过 6节点和18节点算例测试,表明了自适应人工鱼群算法具有更稳定的收敛性能,更高的搜索效率。但是对大规模输电网网架规划的灵敏度还有待于进一步测试和研究。
[1]王锡凡.电力系统优化规划[M].北京:水利电力出版社,1990.
[2]金义雄,程浩忠,严健勇,等.改进粒子群算法及其在输电网规划中的应用[J].中国电机工程学报,2005,25(4):46-50,70.
[3]聂宏展,吕盼,乔怡,等.基于人工鱼群算法的输电网络规划[J].电工电能新技术,2008,27(2):11-15,80.
[4]刘可真,陈勇,束洪春.基于改进遗传算法的输电网优化规划[J].昆明理工大学学报(理工版),2007,32(1):31-35.
[5]吴杰,刘健,卢志刚,等.适用于输电网网架规划的人工鱼群算法[J].电网技术,2007,18(31).
[6]熊信银,吴耀武.遗传算法及其在电力系统中的应用[M].武汉:华中科技大学出版社,2002.

