矩阵求逆的简化算法

李 强

（大庆职业学院工商管理系 黑龙江 大庆 163255）

矩阵理论做为线性代数的主要内容，随着矩阵的应用愈来愈广泛，也倍受重视。 本文仅利用分块矩阵给出矩阵求逆的简化算法，利用定理1 和定理2 可以迅速求出某些矩阵的逆矩阵，提高计算速度。

引理1：设A 为n×n 方阵，且|A|≠o，若A 可分块为A=（）其中A11 是S 阶方阵，A22为t 阶方阵，又A11可逆，则

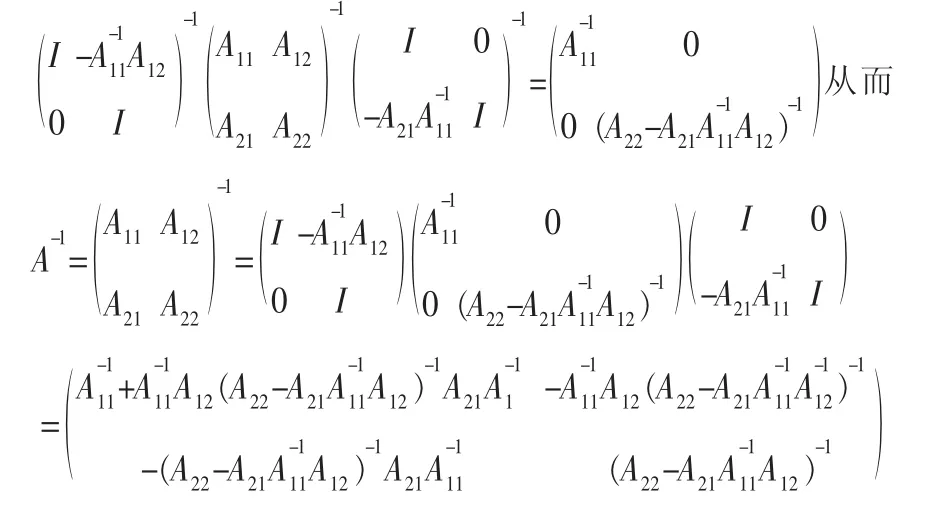
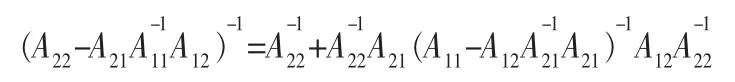
证明：在引理1 证明过程中，设A22可逆，同理可得

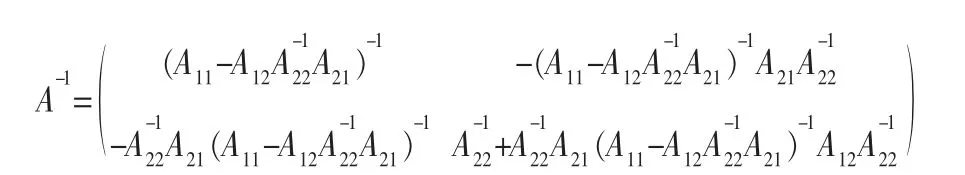
与引理1 比较即得证。

在引理2 中， 设A=A11是n 阶方阵，I=A－122，X=-A12是n×1矩阵，Y=A21是1×n 矩阵，则有

定理1：

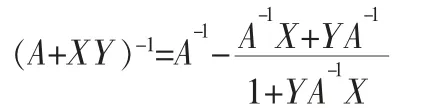
例1

由定理1

定理2：

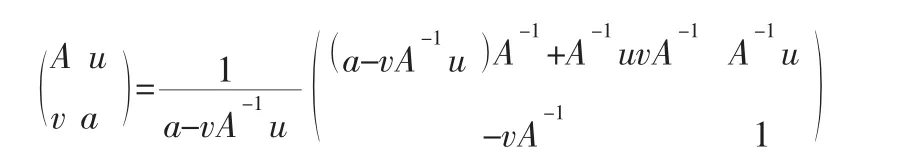
其中A 是n 阶方阵，u 为n×1 矩阵，v 为1×n 矩阵，a≠0。证明类似于定理,略。

例2：

由定理2

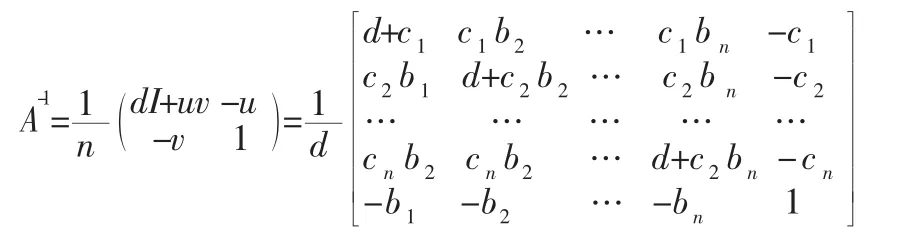
［1］张禾瑞.高等代数[M].高教出版社，1983.

［2］G·W·斯图尔特.矩阵计算引论[M].上海科技出版社，1979.