一种新的变步长LMS 自适应滤波算法及分析
杨晓波
(石家庄职业技术学院电子工程系 河北 石家庄 050081)
0 引言
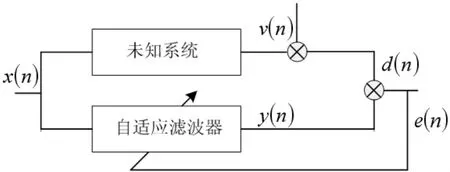
图1 自适应滤波的原理框图
自适应滤波是现代信号处理技术的重要研究领域,自适应滤波技术广泛应用于自适应控制、系统辨识等领域。 图1 为自适应滤波系统辨识的一般原理框图, 衡量自适应滤波算法的主要标准是:初期收敛速度、稳态误差和对时变系统的跟踪能力。 Widrow 等人[1]提出的最小均方误差(LMS)算法因其计算简单、易于实现因而获得了广泛应用,但此算法的缺点是收敛速度和稳态误差性能不能同时得到满足,即选择较大的步长收敛快但稳态误差大,选择较小的步长稳态误差小但是需要较长的收敛时间,对此文献[2、3、4]进行了详细的研究。 由于LMS 算法收敛速度和稳态误差的性能由步长来控制[5],为此人们提出了许多的基于改变步长机制的LMS 算法。文献[6]提出了一种改变步长自适应滤波算法,其步长因子随迭代次数增加而减小,文献[7]提出使步长因子正比于误差信号的大小,文献[8]提出步长和输入与误差之间互相关值成正比,文献[9] 提出了一种步长为Sigmoid 函数的变步长算法 (即SVSLMS 算法)。此算法的优点是在初始阶段或未知系统参数发生变化时步长比较大, 从而有较快的收敛速度; 在算法收敛后,不管主输入干扰v(n)有多大,都保持很小的调整步长从而获得很小的稳态失调噪声。 此算法的缺点是当稳态误差e(n)在接近零处变化时,步长变化太大,使得SVSLMS 算法在自适应稳态阶段仍有较大的步长变化。 为此,文献[10]又在Sigmoid 函数的基础上提出了一种新的步长调整原则,即步长因子μ(n)和误差e(n)之间的新的非线性函数,μ(n)和e(n)的函数关系如下:
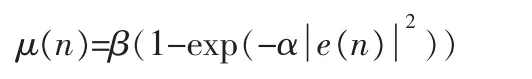
其中,参数α>0 控制函数的形状,参数β>0 控制函数的取值范围,μ(n)和e(n)的函数曲线如图2,图3 所示,该函数比Sigmoid 函数简单,并且在e(n)接近零处具有缓慢变化的特性,在一定程度上克服了Sigmoid 函数的不足。 文献[10]提出的自适应滤波的算法如下:
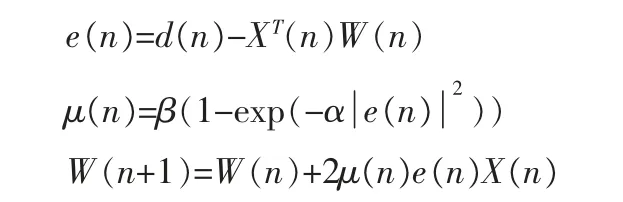
文献[10]中对算法进行了仿真,取得了较好的效果,并验证优于SVLMS 算法。 但是,其算法中控制步长函数形状的参数α 是不变的,图2、图3 是文献[10]的步长因子随误差信号e(n)变化的曲线。
我们从μ(n)和e(n)的函数关系曲线图2、图3 可以看出, μ(n)随e(n)变化的总体规律是当选择较大的α 时算法具有较大的初期收敛步长,但是当e(n)接近零时,步长同样比较大;对于比较小的α 当e(n)接近零时初期收敛步长小,但同时初期收敛步长也较小。 基于以上分析,本文认为在算法的收敛初期可以选择较大的α,取较大的步长,达到较快收敛的目的,而当e(n)接近零时,也就是收敛的后期可以根据一个e(n)的门限Ve 切换到较小的α,以得到较小的稳态误差,这样步长更为理想。
1 一种新的LMS 算法
由此,根据文献[10]提出的步长因子和误差信号的非线性函数,本文提出的一种新的变步长自适应滤波算法如下:

其中Ve 为切换步长因子的时e(n)的门限值,是一个较小的正值,α1和α2分别是切换前后控制函数形状的参数,α2<α1。
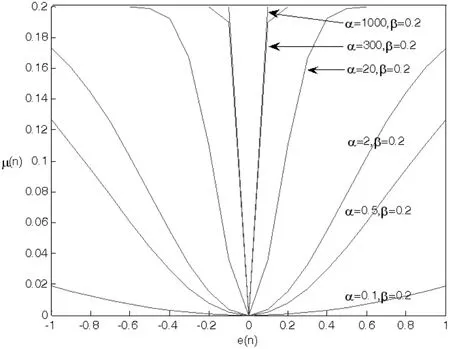
图2 μ(n)和e(n)的关系曲线(α 不同,β 相同)
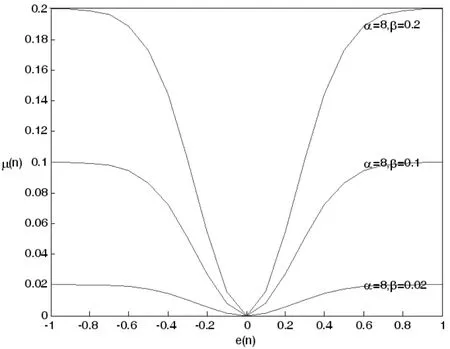
图3 μ(n)和e(n)的关系曲线(α 相同,β 不同)
LMS 自适应滤波的收敛条件是:0<μ<1/λmax,λmax是输入信号的自相关矩阵的最大特征值,由前面的讨论可知参数β(β>0)控制函数的取值范围,所以在β<λmax的条件下,算法一定收敛。 同时由图3 可知,较大的β 值对应较大的步长,所以在满足β<λmax条件下,使β 的值越大越好,因为算法中有步长的切换,所以不用担心稳态误差过大的问题。
图2 是固定β 的情况下变化α 的步长曲线,α 越大对于相同误差信号下步长越大,仿真结果还表明当α>1000 后,步长曲线已没有明显变化, 所以初始收敛时可以令α1=1000,因为算法中有步长的切换, 所以也不用担心α1太大会造成稳态误差过大的问题。
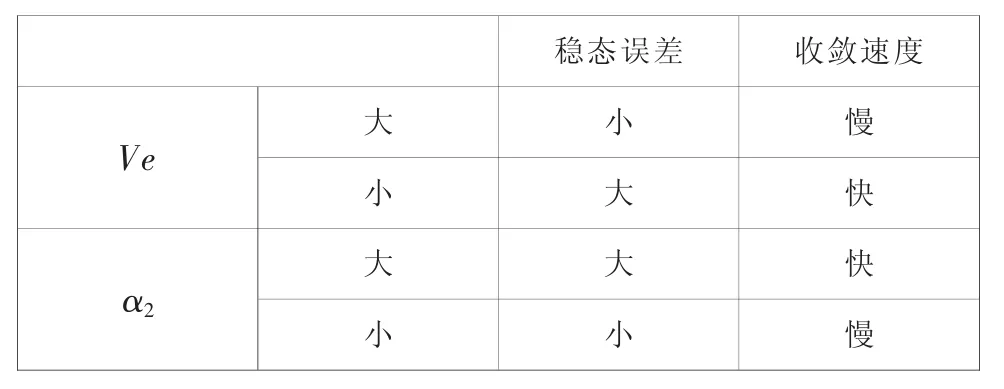
表1 Ve 和α2 对稳态误差和收敛速度的影响
分析图2 可知, 门限Ve 和α2的选择对收敛速度和稳态误差是一个调谐的过程, 下表列出了Ve 和α2的取值对稳态误差和收敛速度的影响。
由表1 可知通过仿真可以根据收敛速度和稳态误差的要求调谐设定Ve 和α2的取值。 当需要小的稳态误差时可以选择较大的Ve 和较小α2, 当需要较快的收敛速度时选择较小的Ve 和较大α2, 当然也可以通过Ve 和α2的调谐同时获得相对较好的收敛速度和稳态误差。
2 计算机仿真结果及分析
为同时获得较快的收敛速度和较小的稳态误差下面通过计算机仿真来确定Ve 和α2, 并检验我们给出的变步长LMS 自适应算法的收敛性以及Ve 和α2的选择对算法收敛性能的影响的分析,为了对比,本文选用文献[10]的仿真条件:
1)自适应滤波器的阶数L=2;
2)未知系统为FIR 滤波器,其系数为W= [0.8,0.5]T,在第500 个采样点时刻系统发生时变,系数变为W= [0.4,0.2]T;
3)参考输入信号x(n)是均值为零,方差为1 的高斯白噪声;
4)v(n)是与x(n)不相关的高斯白噪声,其均值为零,方差为0.04.分别作200 次仿真,采样点数为1000,然后求其平均值,得到学习曲线。
图4 是在α=1000,β=0.2 情况下的收敛曲线(在该实验条件下,文献[10]已经验证β=0.2 为最优),算法在均方误差为0.05 左右收敛,所以Ve 可以在0.05 左右取值,由于e(n)有一定的随机性, 为了不影响收敛速度可以取的稍小于0.05,由图5 的仿真结果可证明取0.03 是合适的。
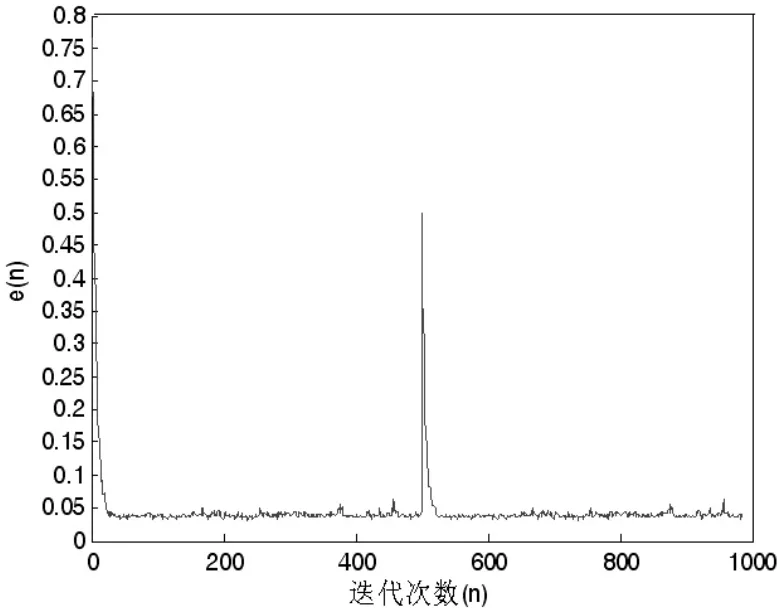
图4 α=1000,β=0.2 收敛曲线
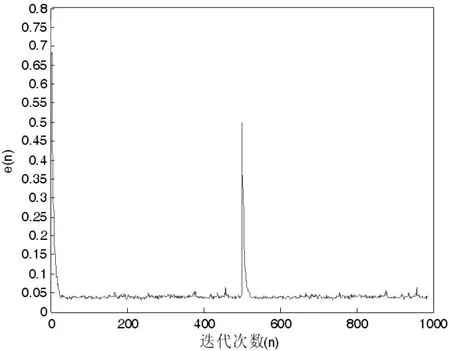
图5 β=0.2,α1=1000,α2=20 情况下Ve 取不同值的仿真曲线
图6 是β=0.2,α1=1000,Ve=0.03 情况下不同α2的仿真曲线,可以看出α2=100 时,算法收敛快,但是稳态误差要大;α2=20 时,算法收敛慢,但是稳态误差要小;中间的曲线为α2=60时情况, 算法收敛速度和稳态误差是前两种情况的折衷,对此, 如果想让收敛速度和稳态误差比较合适可以取为60 左右。 由此可以确定本文算法的参数α1=1000,α2=60,β=0.2,Ve=0.03;
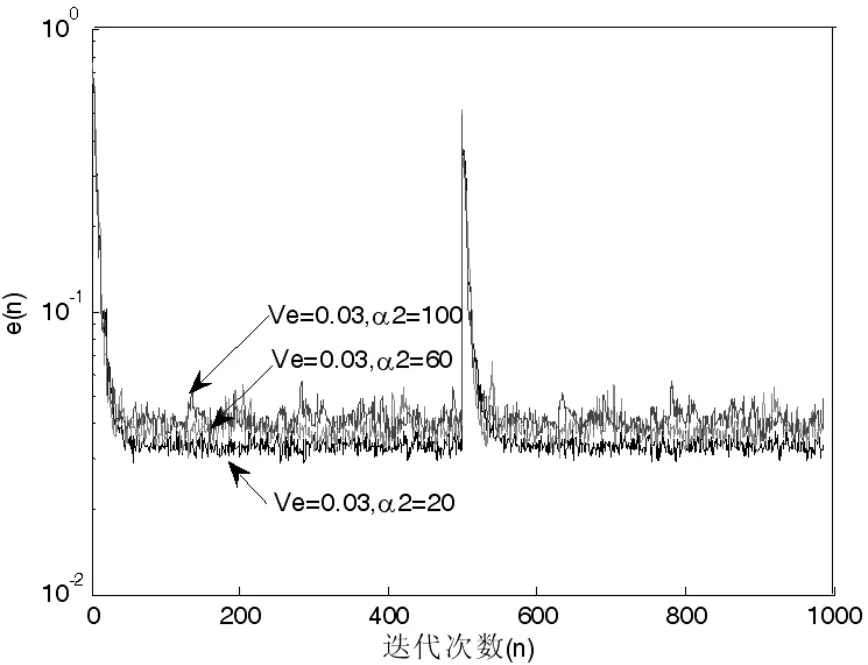
图6 β=0.2,α1=1000,Ve=0.03 情况下不同α2 的收敛曲线

图7 两组不同Ve、α2 的收敛曲线
图5 在α2相同情况下,Ve 越小收敛越快,但是稳态误差越大; 由图6 可知Ve 相同情况下,α2越小收敛越慢,但是稳态误差越小。
图7 是Ve 和α2分别取两组不同值的情况的收敛曲线,Ve=0.03,α2=100 切换门限小,α2大其收敛速度快但是稳态误差较大,Ve=0.5,α2=20 切换门限大,α2小,其收敛速度慢但是其稳态误差小,这和第2 节对Ve 和α2的分析是一致的,证明第2 节的分析是正确的。
3 本文算法和其他文献算法的比较
仍利用上面的实验条件,在此实验条件下文献[10]算法的α=300,β=0.2(最优情况),对于本文算法α1=1000,α2=60,β=0.2,Ve=0.03;
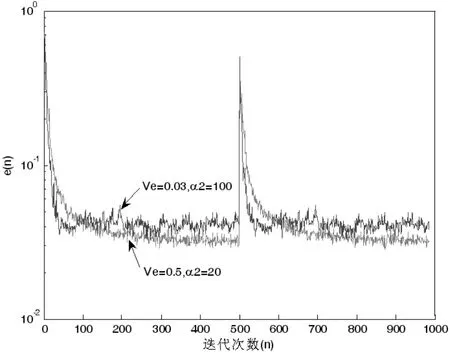
图8 文献[10]算法和本文算法比较
图8 为本文算法和文献[10]算法的比较,可以看出本文算法收敛更快,并且具有更好的稳态。 并且在第500 个采样点时刻未知系统发生变化时,本文算法能比文献[10]算法更快地回到稳态,这说明本文算法具有更好的鲁棒性[11]。
4 结论
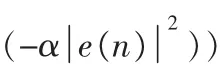
[1]WIDROW B. Adaptive Signal Processing [M] USA: Prentice2Hall Inc., 1985.
[2]WIDROW B ,MCCOOL J M , LARMOR E M G ,JO HN2SON C R. Stationary and non stationary learning characteristics of t he LMS adaptive filter [J ] . Proc IEEE, 1976, 64 (8):l947-l95l.
[3]GEL FAND S B, WEI Y KROGMEI ER J V. The stability of variable step size LMS al-gorithms [J]. IEEE Trans on Signal Processing,l999, 47(l2):3277-3288.
[4]ABOULNASRT M YAS K. A robust variable step size lms type algorithm: Analysis and simulations [J].IEEE Trans on Signal Processing,1997, 45(3):631-639.
[5]GUO L, LJUNG L, WANG G G J.Necessary and sufficient conditions for stability of LMS [J]. IEEE Trans on Automatic Control,1997,42(6):761-770.
[6]Gitlin R. D, Weinstein S. D. On the design of gradient algorithms for digitally implement-ed adaptive filters [J]. IEEE Trans on CT,1973(2):125-136.
[7]R H Kwong, E w Johnston. A variable step size LMS algorithm [J].IEEE Trans Signal processing, 1992,40(7):1633-1642.
[8]T J Shan Kailaith.Adaptive algorithm with an automatic gain control feature[J].IEEE Trans.Acoust,Signal processing,1991,35(1):122-127.
[9]覃景繁,欧阳景正.一种新的变步长自适应滤波算法[J].数据采集与处理,1997,12 (3):171-194.
[10]高鹰,谢胜利.一种变步长LMS 自适应滤波算法及分析[J].电子学报,2001,8.
[11]杨学贤,张群英,侯紫峰.用于ADSL 中的变步长LMS 算法[J].通信学报,2002,23(3):78-83.

