面向智能视频监控系统运动目标检测的轮廓提取方法

谢 立 胡玲玲 吕一品 熊 刚 陈耀武

(1浙江大学信息学部，杭州 310027)(2中国科学院自动化研究所，北京 100190)(3中国科学院云计算产业技术创新与育成中心自动化研究所东莞研究院，东莞 523808)

近年来，随着物联网技术的不断发展，物联网的应用领域不断得以扩大.在公共安全领域，视频监控系统已经获得了很大程度的普及.人们对生活水平日益增长的要求，使得提高智能分析能力已经成为视频监控系统发展的首要任务［1］.运动目标检测作为视频监控系统智能分析的第一步，就是将监视场景中感兴趣的运动目标所对应区域从输入的视频序列图像中分割出来，利用各种特征(如位置、颜色、角点等)来描述该目标［2］.视频序列图像中的运动目标识别、运动目标跟踪、运动目标行为分析等工作均需要依赖于运动目标检测展开，运动目标检测的好坏直接影响到这些后续环节的处理效果.因此运动目标的检测是智能视觉分析中一个十分关键的重要环节，在安防监控、智能交通、航空航天、国防军事等许多领域有着极为广泛的应用.

一般情况下，面向安防的视频监控系统采用静态摄像机对固定区域进行实时监控，获得的监视场景为静止图像背景.因此，可以采用背景建模方法作为运动目标实时分割问题的解决手段［3］.但是由于在视频监控系统中，静态图像背景可能存在着动态变化情况，例如:在视频采集过程中，图像受到光照强度变化、天气雨雪的干扰、相机的移动或微小振动、阴影或反光现象、背景的扰动变化(如树枝的飘动等)，此时，采用传统的背景建模方法有效检测出运动目标将是一件相当困难的工作.

从分析方法上看，运动目标检测方法主要分为帧间差分法、光流法、背景差分法3种类型.① 帧间差分方法，也叫时间差分法［4］，是在图像序列中利用连续的两帧或者三帧图像做像素时间差分，并且阀值化来检测运动目标.帧间差分方法能够很好的适应各种动态环境，但一般无法提取出所有的相关特征像素点，而且运动物体运动快慢都会对提取结果产生影响.② 光流法［5］利用了运动目标随时间变化的光流特性，通过运动估计及运动矢量场信息提取图像中的运动目标.光流法优点是能在摄像机运动情况下检测运动目标.但光流场计算量较大，计算的精确性易受到噪声、光照变化等干扰因素影响，且需要专用硬件设备支持，才能实现目标的实时检测.③ 背景差分法［6］是目前最常用的运动目标检测方法.它的基本思想是利用当前图像与背景图像进行比较，通过比较差分后的灰度或者其他特征的变化来检测出运动区域.提高背景差分法精确度的关键在于建立对环境变化的高度鲁棒和对运动目标的高度适应的背景模型.静态背景模型无法充分描述图像背景.Stauffer等［7］采用自适应混合高斯模型描述图像背景，能够很好地适应外部环境的变化.背景差分能够提供最完全的特征数据，但是对动态场景变化较为敏感.

本文针对传统混合高斯模型方法在智能视频监控系统运动目标检测应用中存在的不足进行改进研究，提出一种新的运动目标轮廓提取方法.

1 轮廓提取方法

1.1 传统混合高斯模型方法

混合高斯模型的基本思想为:对于静止或缓慢变化的背景，可以用正态分布来描述像素点灰度值的变化［8］.使用K个高斯混合模型的线性组合来表征视频序列每帧图像中每个像素点的特征，每获得一帧新的图像，高斯模型就进行相应的学习和更新.将混合高斯模型与当前帧图像上的每一个像素点进行匹配，当匹配成功时判定该像素是为背景点，反之则认为该像素点是前景点.

定义当前像素点灰度值的概率为

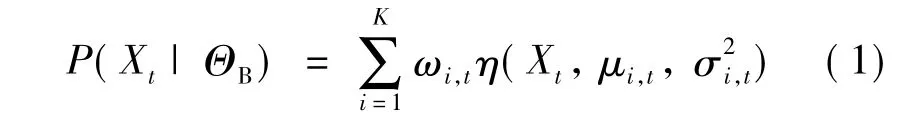
式中，Xt为t时刻该像素的灰度值或颜色矢量；P(Xt|ΘB)为当某个像素点的像素值为Xt时，它属于背景ΘB的似然概率；K为混合高斯模型中用来表征像素特征的高斯分量的数目，一般选择3～5之间；ωi，t为t时刻混合高斯模型中第i个高斯模型的权重，且ωi，t=1；μi，t为 t时刻混合高斯模型中第i个高斯分量的均值；为 t时刻混合高斯模型中第i个高斯分量的方差；η为t时刻混合高斯模型中第i个高斯分量的高斯概率密度函数，满足:

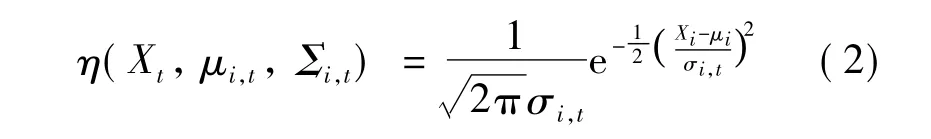
混合高斯模型方法使用在线递归EM估计技术来逐帧更新图像的背景模型参数，实现背景模型的在线学习和更新.在混合高斯模型中，各模型分量的权重通常是不一致的.按照从大到小对高斯分量进行排序，按下式选取前B个分量组成混合高斯背景模型:

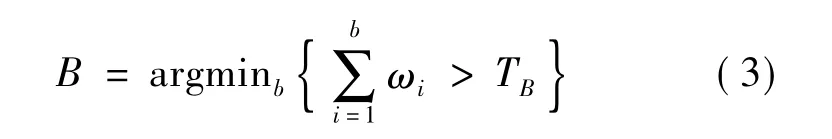
其中，TB∈［0，1］，用来决定模型中高斯分量的个数.

将当前图像中的每一个像素点与之前获得的B个高斯分量按下式逐一进行匹配:

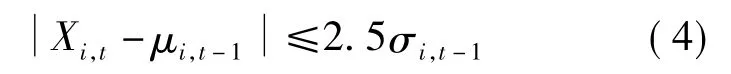
式中，参数更新率 0≤α≤1，ρ= α/ωi，t；匹配成功时，Mi，t=1，否则 Mi，t=0.

如果像素Xi，t与混合模型中的任何一个高斯分量都不匹配，则新定义一个高斯分布(均值为Xi，t，方差自定义)代替权值最低的高斯模型分量.

传统的混合高斯模型方法能够有效地提取出监控视频的前景目标，但是通过对大量监控视频的测试实验，发现传统高斯背景模型方法存在以下缺点:

1)高斯混合模型背景建模方法是以单个像素形式进行描述，每个像素进行独立的假设使得监视场景的空间结构信息损失，导致系统运算效率不高；

2)高斯混合模型背景建模方法比较容易受到外界干扰，如光源变化、摇曳的树叶等因素的影响，使得前景图像存在着噪声.

为了解决上述缺点，提出如下方法加以解决.

1.2 像素块混合高斯模型方法提取前景目标

针对传统的混合高斯模型方法运算效率不高的缺点，提出像素块高斯混合模型背景建模方法，来提高系统运算速度.因为相邻像素点之间存在着一定的空间冗余信息.例如，背景中相邻像素会同时反映出外界的光线变化.在背景图像中相互间具有稳定关系的像素占有相当大比例，导致以单像素形式建立的背景模型存在着大量冗余计算.本文将每帧图像分割成m×n个相邻像素的矩形块.矩形块越大，一帧图像需要处理的块数就越少，系统计算速度就越快，但对前景目标的精确度就会变差.因此，需要通过大量现场实验数据测试，权衡识别目标的精确性和图像处理效率，来确定像素块大小.

此时，每个像素块可以表示为K个高斯分布模型的线性组合:

当像素与某高斯分量的差值满足上式，则与该高斯分量相匹配，该像素为背景点，否则为前景点.

匹配后，需要对所有高斯分量进行更新:

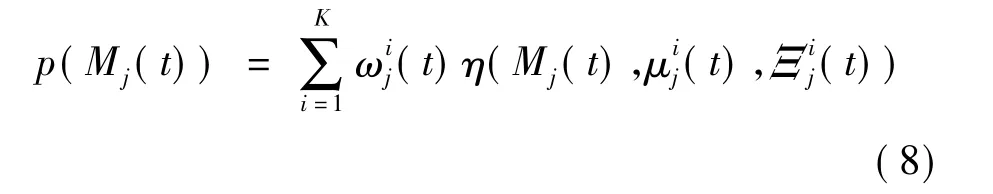
式中，Mj(t)为第j个图像块在t时刻的像素均值；(t)为第i个高斯成分的均值；(t)为第i个高斯成分的协方差矩阵；(t)为混合高斯模型中第i个高斯成分的权值估计.

随着场景的变化，每个像素块的混合高斯模型都需要不断地学习更新.高斯成分中权值、均值、协方差矩阵，都按照传统混合高斯背景模型的更新方法进行更新.对未匹配成功的分量中的高斯分布参数方差和均值不做修改，只修改与新的图像帧数据相匹配的模型参数.

1.3 数学形态学方法进行前景连通

针对传统的混合高斯模型方法获得的前景图像存在干扰噪声的缺点，利用形态学方法对前面提出的像素块混合高斯模型方法获得的前景目标进行前景连通［9］，一方面利用形态学的开闭操作清除前景噪声；另一方面对已有的轮廓进行处理，提取并合成轮廓，从而有效地提取出感兴趣的目标轮廓区域.

在连通过程中，采用腐蚀方法(9)用于消除前景图像中的斑点噪声，采用膨胀操作(10)将被噪声、阴影分离的同一目标再次融合在一起.

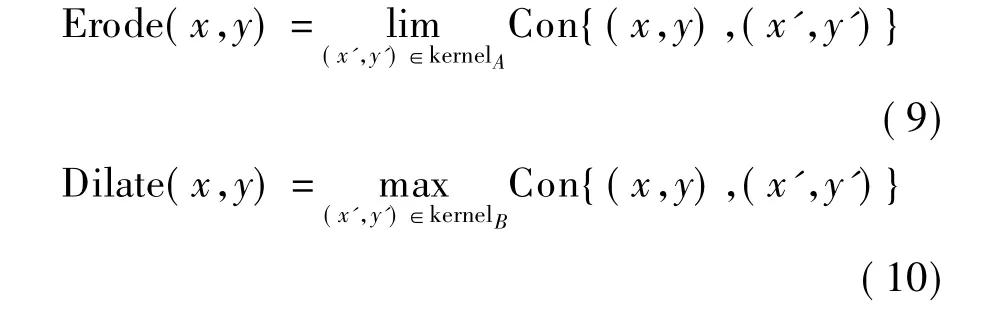
在腐蚀的过程中，图像和核A进行卷积，取局部最小值，并将其赋给参考点指定的像素点，腐蚀可以消除目标的小凸起.而在膨胀的过程中，前景目标与核B进行卷积，取局部最大值来赋予参考点指定的像素点，膨胀可以填补目标的凹洞.

1.4 Freeman链码寻找轮廓

利用Freeman链码来表示前景目标对象各点之间相邻位置的矢量关系［10］，即目标边缘上相邻两像素点之间的位置关系有水平、垂直、斜对角共8 个方向，可分别用0，1，2，3，4，5，6，7 八个字符表示.在本方法中，以N×N像素块(N的大小根据设计要求给定)为基本单元，从某点开始，沿着目标轮廓计算每一个像素块的走向并且用相应的方向字符进行表示，其中偶数字符代表垂直或水平线段，奇数字符代表对角线线段.经过上述处理，就能够得到一组记录起始点的坐标和位置方向的Freeman链码序列点，连接这些点就能构成了目标的轮廓.

若Freeman链码序列长度小于预先给定的值，则认为该轮廓面积较小，将该轮廓丢弃.

1.5 Douglas-Peucker算法拟合轮廓

Douglas-Peucker算法的基本思想是:通过预先设定精度，利用直线对曲线进行不同程度的逼近，其精确程度由弧与直线之间的最大距离来表示［11］.

DP算法利用迭代的思想，在预先给定距离容差的情况下，连接弧线首尾两点，构成直线；逐个计算弧中个点到直线的距离，找出距离最大的点，将其和距离容差进行比较，如果小于距离容差，则舍去中间点，用直线代替弧线，如果大于距离容差，则保留该点，同时将曲线从该点一分为二，重复上述过程.通过DP算法，可以得到目标区域的轮廓.

1.6 基于图像矩的质心提取

质心利用矩的原理来进行计算，一个目标轮廓的(p，q)矩的定义如下:

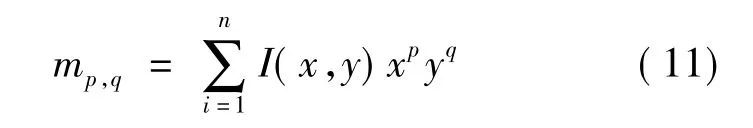
当图像为二值化轮廓图时，m00为轮廓的边界长度［12］.

由此引申开来，可以得到一个图像的中心矩为

1.7 轮廓提取方法流程

根据以上的分析，本文提出的轮廓提取方法的算法流程为:首先，针对运动目标所在监视场景的图像序列进行像素块混合高斯背景建模，获得前景区域(即运动目标所占区域)，此时得到的前景中含有噪声或其他干扰有关的小轮廓；为了获取干净的目标信息，采用数学形态学方法对前景图像进行腐蚀和膨胀处理，以去除噪声；接着，利用Freeman链码对目标进行轮廓提取，并计算凸包，去除小的轮廓；再利用Douglas-Peucker算法对目标轮廓进行凸包拟合，输出面积最大的目标轮廓；最后，利用矩方法计算轮廓的质心c，从而得到目标的质心位置，为后续的运动目标跟踪处理提供必要的特征信息，见图1.

2 实验结果

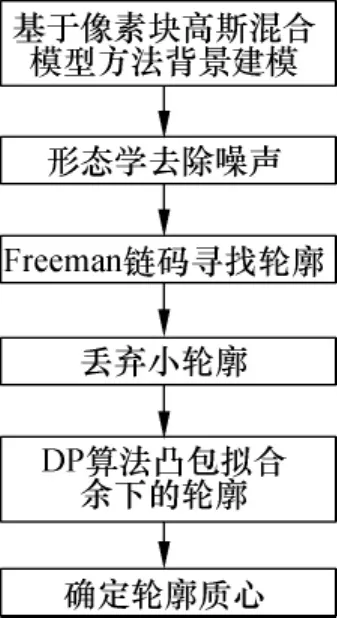
图1 本文的轮廓提取方法流程图

在本节中，对前面提出的轮廓提取算法进行实验验证.首先，使用传统的高斯混合模型方法进行运动目标轮廓提取，应用效果如图2所示.

图2 传统高斯混合模型方法的目标轮廓提取效果

图2中，传统的高斯混合模型背景建模方法能够提取出前景目标轮廓，但是效果不太好.主要原因在于:在最初高斯混合模型参数更新过程中，如果背景中有边缘，或者是摇曳的树叶，比如图2的树叶和墙的边缘，就有可能被建模到前景中；同时，在最初的几帧中，前景物体会被建模到背景中，导致前景图像效果下降.由于高斯混合模型背景建模方法需要一定的时间学习，前景图像中类似的噪声需要一定处理时间才能消除.

采用本文提出的算法进行目标轮廓提取，实验效果如图3所示.由图可见.利用前景连通，有效地滤除了不必要的噪声和细小轮廓，通过本文提出的算法流程，可以准确找到感兴趣的运动目标区域，目标轮廓物体被准确、有效地提取出来.

图3 本文提出算法的目标轮廓提取效果

3 结语

本文针对传统的混合高斯模型方法易受干扰、运算量大的缺点，提出一种应用于智能视频监控系统运动目标检测的轮廓提取方法.该算法依次采用像素块混合高斯模型方法提取前景目标，数学形态学方法进行前景连通，Freeman链码寻找轮廓，Douglas-Peucker算法拟合轮廓，图像矩提取目标轮廓质心.最后通过实验证明，本文提出的算法能有效地滤除噪声，准确地提取出目标轮廓，实验效果优于传统混合高斯模型方法，为进一步增强智能视频监控系统的视频分析的可靠性提供了有益的技术支撑.

References)

［1］Hu W，Tan T，Wang L.A survey on visual surveillance of object motion and behaviors［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part C:Applications and Reviews，2004，34(3):334-352.

［2］Chacon-Murguia M I，Gonzalez-Duarte S.An adaptive neural-fuzzy approach for object detection in dynamic backgrounds for surveillance systems［J］.IEEE Transactions on Industrial Electronics，2012，59(8):3286-3298.

［3］Spagnolo P，Orazio T D，Leo M.Moving object segmentation by background subtraction and temporal analysis［J］.Image and Vision Computing，2006，24(5):411-423.

［4］Bennett B，Magee D R，Cohn A G，et al.Enhanced tracking and recognition of moving objects by reasoning about spatio-temporal continuity［J］.Image and Vision Computing，2008，26(1):67-81.

［5］Dacron J，Fleet D，Beachemin S.Performance of optical flow techniques［J］.International Journal of computer Vision，1994，12(1):42-47.

［6］Benezeth Y，Jodoin P M，Emile B，et al.Review and evaluation of commonly-implemented background subtraction algorithms［C］//International Conference on Pattern Recognition.Florida，USA，2008:1-4.

［7］Stauffer C，Grimson W.Adaptive background mixture models for real-time tracking［C］//Proceeding of IEEE Conference on Computer Vision and Pattern Recognition.Fort Collins，USA，1999，2:246-252.

［8］Sheng Z B，Cui X Y.An adaptive learning rate GMM for background extraction［J］.Optoelectronics Letters，2008，4(6):460-463.

［9］Shih F Y.Image processing and mathematical morphology:fundamentals and applications［M］.New York:CRC Press，2009.

［10］Saghri J A，Freeman H.Analysis of the precision of generalized chain codes for the representation of planar curves［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1981，3(5):533-539.

［11］Visvalingam M，WhyattArticle J D.The Douglas-Peucker algorithm for line simplification:re-evaluation through visualization［J］.Computer Graphics Forum，1990，9(3):213-225.

［12］Abu-Mostafa Y S，Psaltis D.Image normalization by complex moments［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1985，7(1):46-55.