基于局部加权k近邻的多机器人系统异步互增强学习

杨月全 韩飞 金露 倪春波 曹志强 张天平

(1扬州大学信息工程学院，扬州 225009)(2中国科学院自动化研究所复杂系统管理与控制国家重点实验室，北京 100190)

多机器人系统已成为当前国内外机器人领域研究的热点.由于机器人所面临的环境往往是未知的、动态的，因而通过人为的规划来解决多机器人系统中所遇到的一切问题是不现实的.在这种情况下，学习能力为机器人克服这些困难提供了行之有效的方法.机器人的学习可主要通过以下方式进行［1］:借助于自身的各种传感器，机器人可以在与环境的不断交互中获取知识；借助一些领域知识、先验知识来缩短学习时间；通过与其他机器人共享知识促进彼此的技能；模拟进化的有关思想来对自身的参数进行优化.

增强学习是一种以环境反馈作为输入的机器学习方法［2］.文献［3］提出了一种新的多智能体Q学习算法，通过对联合动作的统计来学习其他智能体的行为策略，并利用智能体策略向量的全概率分布保证了对联合最优动作的选择.文献［4-6］引入能体现人的经验的模糊推理规则来改进机器人学习.文献［7］提出了连续状态空间中 kNN-TD算法，从状态分类的角度来加快学习速度.文献［8］提出了一种未知环境下基于有先验知识的滚动Q学习算法.文献［9-10］基于TD算法，提出了快速强化学习方法和自然梯度强化学习算法.在此基础上，基于局部加权 kNN-TD 算法［7，11-14］，本文提出了多机器人系统的无时滞异步的互增强学习策略.在全局通信和局部通信情况下，机器人通过比较自身和通信范围内的机器人Q值表，进行选择最优动作，实现无时滞条件下的多机器人系统的异步的交互增强学习.最后，仿真实验进一步验证了所提方法的可行性和有效性.

1 局部加权kNN-TD算法［14］

设机器人状态为 s=［sd，sg］=［ρ1，ρ2，…，ρ12，sg］，其中 sd=［ρ1，ρ2，…，ρ12］表示环境信息，sg为目标位置信息，ρ表示相应传感器工作区域范围内是否存在障碍，当在范围l0内探测到障碍时，取值1；否则，取值0.建立以机器人为原点、前进方向为x轴正向、逆时针旋转90°方向为y轴正向的坐标系.设机器人所处位置为(xp，yp)，其方向角为θp，目标点位置为(xg，yg).得到目标相对于机器人的位置(x'g，y'g)为

则机器人指向目标点的方向角θg=atan(y'g/x'g).由于机器人的状态数目过大，学习耗时很大，为此引入kNN-TD算法［7］.根据机器人前后左右的各部分状态对其影响各不相同，将环境信息划分为4 个部分，并配以不同的权重 ηp，p=1，2，3，4.对于目标位置信息sg相同的状态si和sj，定义其距离函数为

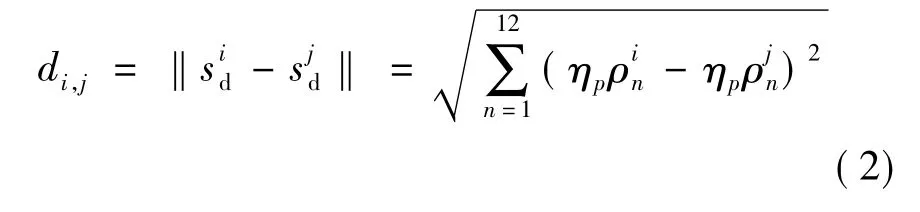
式中，di，j表示状态 si，sj的环境信息状态的差别.选取最小的前k个di，j的状态为状态si的近邻，记为knn(si)；同时易得其每一个近邻的权值为ωi，j=1/(1+).在此基础上，可求得状态 sj是状态si近邻的概率为

设si∈S，am∈A，其中 S为状态集，A为动作集，knn(si)表示状态 si的 k 近邻集，Q(si，am)表示状态si下动作am的Q值.考虑近邻的影响，定义Qknn(si)(si，am)为状态si在选择动作am时近邻集knn(si)的Q值期望，其可表示为

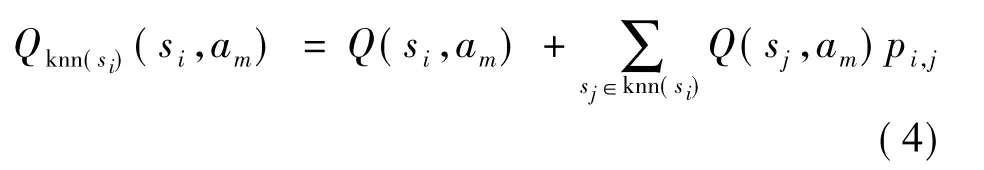
在初始阶段，采取基于模拟退火的动作选择机制策略.状态si的每一个动作被选的概率如下:

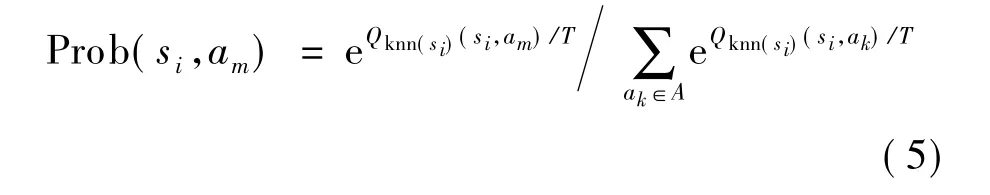
式中，T为退火温度，取值逐渐减小，T的大小决定了随机性的程度，T越大，随机性越大，反之越小.随着学习的进行，动作选择机制换为贪婪策略，即

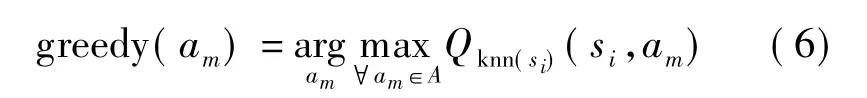
考虑机器人在状态si下执行选择动作am，并转移到一个新的状态sk，并获得奖赏 r.利用近邻集Q值函数［7］，得到状态si下的Q值函数更新规则

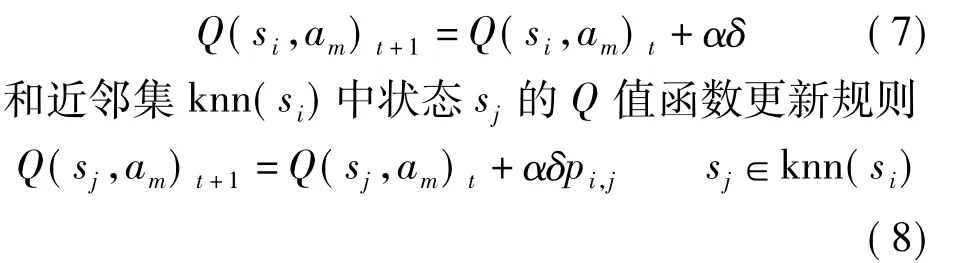
式中，α∈(0，1)为学习率；δ为 TD 误差.基于 TD算法，这里采用无策略(off policy)法，δ可表示为

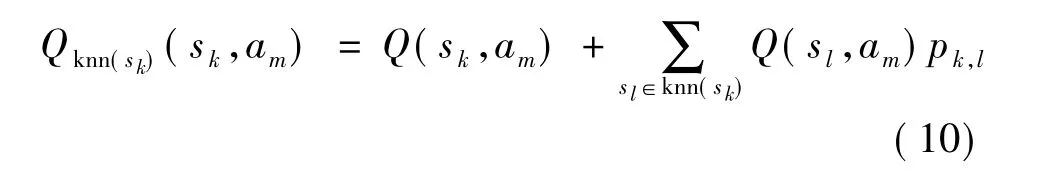
2 基于全局通信条件的异步互增强学习

考虑传统增强学习过程中，每个机器人都有其独立的Q值表，Q值表更新由其自身反馈而决定.在全局通信条件下，机器人通过比较自身和通信范围内的机器人Q值表，进行选择最优动作.设未知环境中存在N个机器人，机器人间可实现无时滞通信，记为 Φ={Rbb=1，2，…，N}.确定机器人Rb的Q值更新规则为

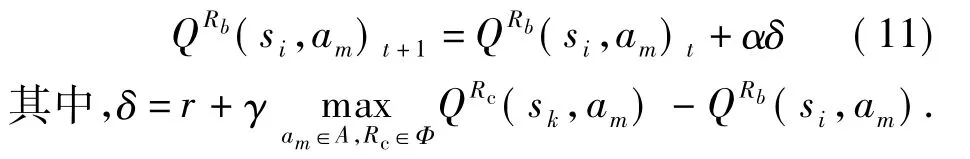
由局部加权kNN-TD算法，可得到机器人Rb的状态si下的Q值函数更新规则

和其近邻集knn(si)中状态sj的Q值函数更新规则

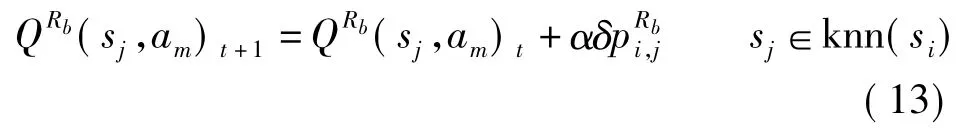
式中，α∈(0，1)为学习率；δ为 TD 误差.δ可表示为

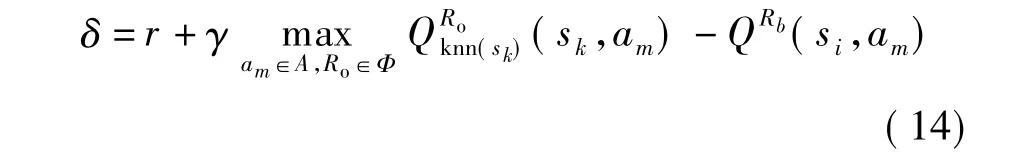
由此可得，机器人Rb在状态sk的取动作am时的近邻集knn(sk)的最大Q值期望为

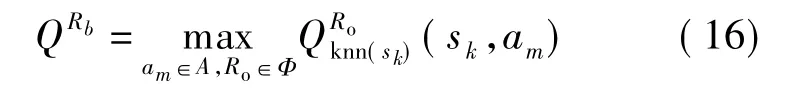
3 基于局部通信条件下的异步互增强学习

在大多数实际环境中，一方面通讯往往非全局的，另一方面随着机器人数目增加，共享全局信息会增加计算量，且大量的数据通讯会造成信息堵塞.因而单体机器人往往只能与周围一定范围内的机器人进行资源共享.考虑在局部通信条件下多机器人增强学习问题，设单体机器人通讯半径为c.设在t时刻，机器人Rb为中心的通讯范围内存在M个机器人，记为Φb={Rbb=1，2，…，M}，并设机器人间实现无时滞通信.则可设计机器人Rb的Q值更新规则为

不难得到机器人Rb的状态si下的Q值函数更新规则与式(12)相同；另外，其近邻集knn(si)中状态sj的Q值函数更新规则与式(13)相同.这里，可进一步得到δ为

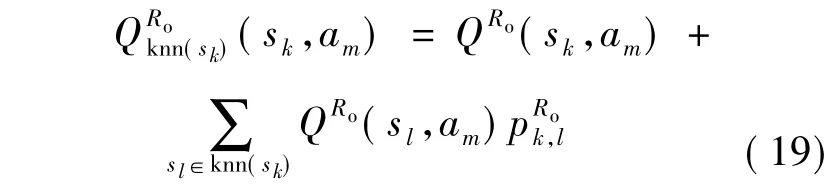
由此可得，机器人Rb在状态sk的取动作am时的近邻集knn(sk)的Q值期望为

4 仿真实验

为验证本文算法的有效性，将3个机器人R1，R2，R3放置于未知环境中，并设置参数如下:近邻个数k=12，传感器探测范围l0=3，环境状态各部分权重 η1=5，η2=10，η3=5，η4=1，学习率 α =0.4，折扣因子γ=0.5，如图1所示.

图1 多机器人学习环境

实验1 在全局通信的情况下，学习是分别给定机器人目标位置，让其自主运动，每个学习阶段运动200步，经过近40次的学习后，机器人R1，R2，R3能较好地运动到目标点.由于本实验中机器人的状态数目过于庞大(212×12)，要达到最优的学习效果还需数以亿次的学习；但本算法只通过约8000步学习即取得了较好的学习结果，实验表明基于局部加权kNN-TD算法的全局通信条件下的多机器人互增强学习效果较优，如图2所示.

实验2 在局部通信的情况下，设机器人的通信半径c=5.在局部通信下，虽然机器人的学习比全局通信条件下慢，但从仿真实验可以看出，机器人仍可较快地完成学习任务，如图3所示.

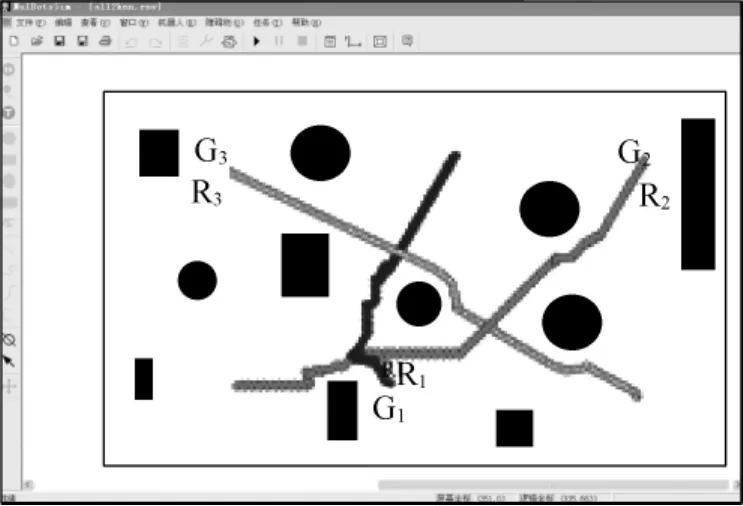
图2 全局通信条件下的异步互增强学习测试

图3 局部通信条件下的异步互增强学习测试

5 结语

针对多机器人系统的增强学习问题，首先基于环境感测和任务信息状态，提出了k近邻状态选择方案；在此基础上，分别给出了全局通信和局部通信条件下的基于局部加权kNN-TD的多机器人系统的无时滞异步的互增强学习策略.下一步的主要工作是进一步完善异步的交互学习策略，并进行相关学习算法的性能比较研究；在此基础上，对多机器人系统的增强学习算法的收敛性分析进行研究.

References)

［1］谭民，王硕，曹志强.多机器人系统［M］.北京:清华大学出版社，2005.

［2］高阳，陈世福，陆鑫.强化学习研究综述［J］.自动化学报，2004，30(1):86-100.Gao Yang，Chen Shifu，Lu Xin.Research on reinforcement learning technology:a review［J］.Acta Automatica Sinica，2004，30(1):86-100.(in Chinese)

［3］郭锐，吴敏，彭军，等.一种新的多智能体Q学习算法［J］.自动化学报，2007，33(4):367-372.Guo Rui，Wu Min，Peng Jun，et al.A new Q learning algorithm for multi-agent systems［J］.Acta Automatica Sinica，2007，33(4):367-372.(in Chinese)

［4］张汝波，施洋.基于模糊Q学习的多机器人系统研究［J］.哈尔滨工程大学学报，2005，26(4):477-481.Zhang Rubo，Shi Yang.Research on multi-robot system based on fuzzy Q-learning［J］.Journal of Harbin Engineering University，2005，26(4):477-481.(in Chinese)

［5］Desouky S F，Schwartz H M.Schwartz.Q(λ)-learning fuzzy logic controller for a multi-robot system［C］//IEEE International Conference on Systems，Man and Cybernetics.Istanbul，Turkey，2010:4075-4080.

［6］Hu Zhaohui，Zhao Dongbiao.Reinforcement learning for multi-agent patrol policy［C］//The 9th IEEE International Conference on Cognitive Informatics.Beijing，China，2010:530-535.

［7］Martin J A H，de Lope J，Maravall D.Robust high performance reinforcement learning through weighted k-nearest neighbors［J］.Neurocomputing，2011，74(8):1251-1259.

［8］胡俊，朱庆保.未知环境下基于有先验知识的滚动Q学习机器人路径规划［J］.控制与决策，2010，25(9):1364-1368.Hu Jun，Zhu Qingbao.Path planning of robot for unknown environment based on prior knowledge rolling Q-learning［J］.Control and Decision，2010，25(9):1364-1368.(in Chinese)

［9］童亮，陆际联，龚建伟.一种快速强化学习方法研究［J］.北京理工大学学报，2005，25(4):328-331.Tong Liang，Lu Jilian，Gong Jianwei.Research on fast reinforcement learning［J］.Transactions of Beijing Institute of Technology，2005，25(4):328-331.(in Chinese)

［10］陈圣磊，谷瑞军，陈耿，等.基于TD(λ)的自然梯度强化学习算法［J］.计算机科学，2010，37(12):186-189.Chen Shenglei，Gu Ruijun，Chen Geng，et al.Natural gradient reinforcement learning algorithm with TD(λ)［J］.Computer Science，2010，37(12):186-189.(in Chinese)

［11］A k-NN based perception scheme for reinforcement learning［J］.Lecture notes in Computer Science，2007，4739:138-145.

［12］Martin J A H，de Lope J.Ex＜α＞:an effective algorithm for continuous actions reinforcement learning problems［C］//The 35th IEEE Annual Conf on Industrial Electronics Society.Oporto，Portugal，2009:2063-2068.

［13］Martin J A H，de Lope J，Maravall D.The kNN-TD reinforcement learning algorithm［J］.Lecture Notes in Computer Science，2009，5901:305-314.

［14］韩飞，金露，杨月全，等.基于局部加权kNN-TD增强学习的机器人运动控制［C］//第十届全球智能控制与自动化大会.北京，2012.(待发表)Han Fei，Jin Lu，Yang Yuequan，et al.Research on robot motion control based on local weighted kNN-TD reinforcement learning［C］//The 10th World Congress on Intelligent Control and Automation.Beijing，2012.(to appear)