基于极坐标的摄像机标定

方旭 达飞鹏 郭涛

(东南大学自动化学院，南京 210096)

摄像机标定是计算机3D视觉测量领域的工作基础，它的本质是解决世界坐标上点的位置和图像坐标上点对应的像素之间的映射关系［1-2］.

大多数标定板是基于直角坐标系设计，本文提出了基于极坐标设计的标定板，并解决了多摄像机标定板的设计问题.有些图像使用直角坐标系表示十分复杂或者根本无法表示，如玫瑰线、阿基米德线等.对于这些难以用直角坐标表示的图像，基于直角坐标寻找匹配点对的方法很难识别.但是这种曲线的特征往往十分明显，有适合当作特征点的点对来用于提取和匹配，因此引入极坐标来表示世界坐标中特征点的位置关系，通过极坐标获得特征点后再将其转换为直角坐标系.这样，在基本不增加系统复杂度的情况下，还可以使用传统的标定方法［1-3］.

使用极坐标的另一个优势是使用较少的点对完成系统的标定，使用最少点对或较少点对完成系统的标定并获得准确结果是最近研究的热点［4］.本文使用的极坐标图像的特征点大概在10～20个，最终得到的标定结果与文献［1］较接近.

极坐标图像也适合于多摄像机标定.多摄像机标定板的制作一直是个难题.三维标定物存在遮挡问题；二维标定板由于要在多个位置的摄像机拍摄范围内，制作要求较复杂，所以杨剑等研究了二维柔性拼接标定板［5-6］；王亮等［7-10］研究了基于一维的多摄像机标定物来解决上面的问题，但是存在运动限制的问题；此外，也有通过经纬仪精确获得物体之间或者摄像机之间的相对位置关系［11］，但是需要额外的仪器和复杂的操作.由于极坐标图像位置的相对关系简单，可以很方便地用于制作成多摄像机的标定板，也可以根据摄像机的摆放来布局极坐标标定板的设计，以此来降低标定板的制作难度和简化标定的复杂度.

1 摄像机模型

摄像机模型是光学成像几何的简化，最常用的摄像机模型是针孔透视模型，如图1所示.摄像机的位置在摄像机坐标下，拍摄在世界坐标系下的图像，获得在摄像机成像平面的图像.该图像在计算机上看是按照计算机图像坐标系成像的图像.最终根据世界坐标系和计算机坐标系下同一个物体上的对应特征点对，求取摄像机的参数.获得2个或多个摄像机参数后，仿真人眼就可以恢复出物体的三维形貌.

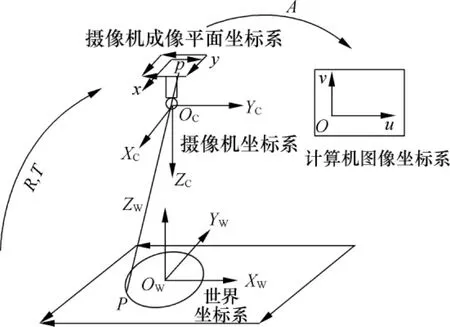
图1 针孔投影模型图

1.1 极坐标及多摄像机标定

标定的简要流程图如图2所示.

1.2 摄像机内外参

世界坐标和计算机坐标下的映射关系H可以表示为列向量形式:

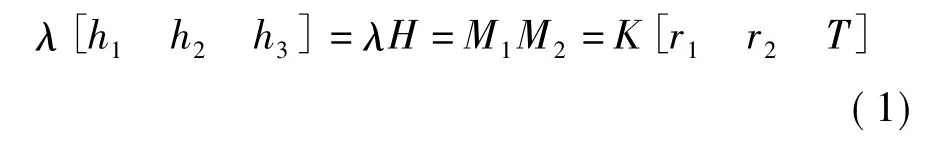
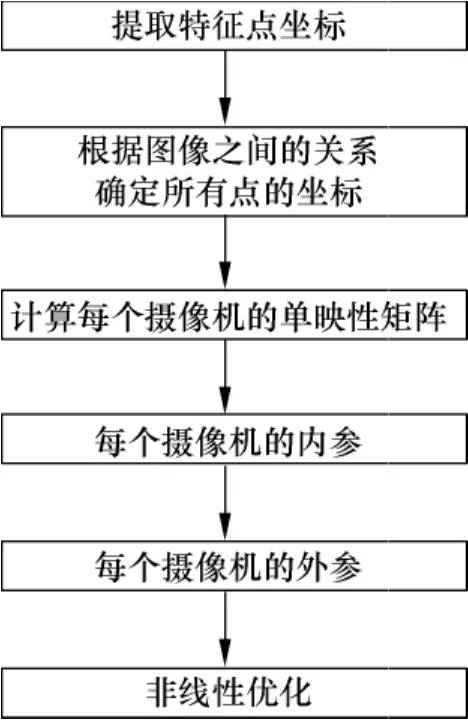
图2 流程图

因为r1和r2是旋转矩阵R的旋转向量，存在r2=0和‖r2‖=‖r1‖，根据这2个等式有

根据方程组(2)可知，每幅图像存在2个方程，而内参K有5个未知数，所以需要不少于3幅图像就可以解出内参.若超过3幅求得的是一个最优解，少于3幅需要1个或3个附加约束条件.得到内参K后，根据式(1)可以获得外参.通常，获得的解不满足旋转矩阵的性质，具体优化可以参考文献［1，12］.

这样获得的内外参只是个粗糙解，没有考虑到镜头畸变.根据 Tsai［2］的分析，考虑径向畸变 k1和k2可以满足普通摄像机的情况.k1和k2的求取可参考文献［13］.在加入畸变后的非线性优化的目标函数为

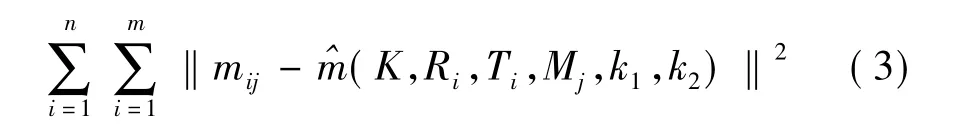
式中，^m(K，Ri，Ti，Mj，k1，k2) 是第 i幅图像上第 j个点计算出来的投影点，mij代表实际所在的位置，上标n代表图像的个数，m代表点的个数.

1.3 多摄像机标定

由于极坐标存在简单的变换关系，所以可以很方便地用于多摄像机标定.比如，标定板可以设计为如图3所示的通过图像各自中心的关系(rij，θij)，很容易确定极坐标图像上各个点的绝对位置信息.

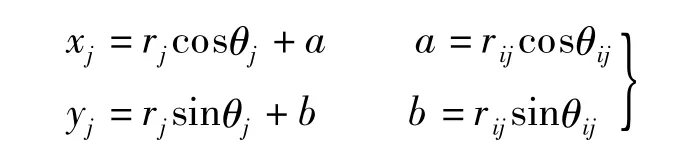
多摄像机标定时不再要求有共同区域:比如摄像机1以图3中极坐标中心1为“世界坐标中心”，摄像机2以极坐标2为“世界坐标中心”，摄像机3以极坐标3为“世界坐标中心”.2和3所指的世界中心，是指摄像机拍摄时的图像中心大概所在位置，这样的布置可以随着摄像机所在的位置对标定板做改变，即(ri，θi)的位置不是事先固定，而是在拍摄时或拍摄完以后才确定.这样解决了基于平面或者立体标定板的多摄像机标定的旋转平移转换带来的误差.如图3所示，极坐标中心1的世界坐标是(0，0)，极坐标中心2的世界坐标为(24，18)，极坐标中心3的世界坐标为(48，－36)，即世界坐标实际是同一个世界坐标.传统的多摄像机标定需要摄像机两两之间存在公共可视区域［10，14］，而本文提出的方法可以不存在公共可视区域.这是因为没有把摄像机非完全会聚配置而导致的数据缺失问题考虑进去.不考虑的原因是标定板标定的距离比重建时物体所在的距离要近，不存在或很少存在数据缺失问题.这样虽然降低了准确度，但是在拍摄的灵活性上有了很大的提高.

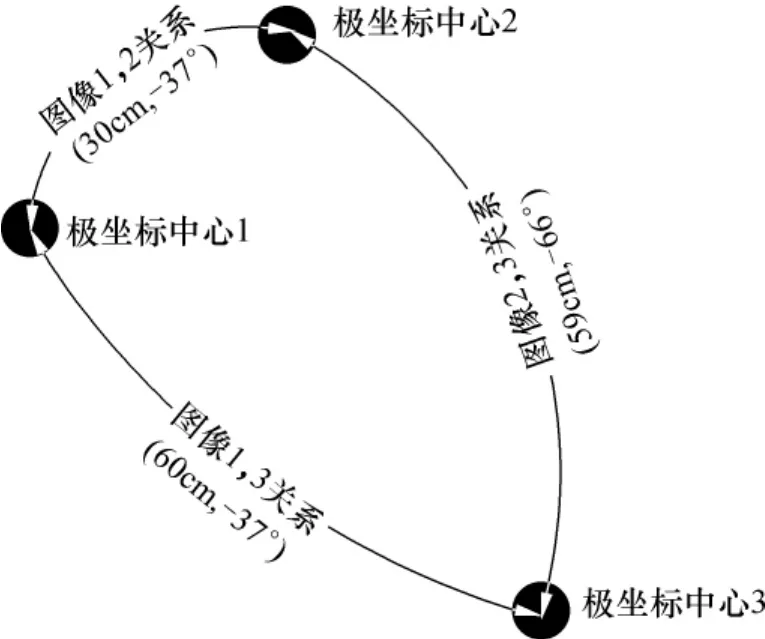
图3 已知各自关系的标定版

2 实验

2.1 仿真实验

在下列仿真实验中，以阿基米德曲线作为标定物.ρ=θ(θ=0～6π).在 θ为45°整数倍且大于等于225°情况，总共取12个点作为特征点.

内参矩阵为

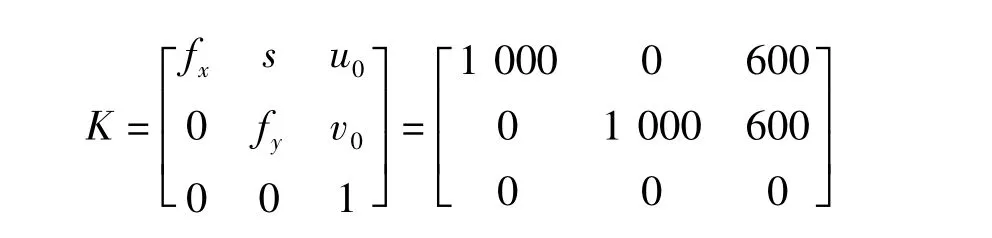
3幅图的外参分别为

第 1 幅图:α1=16.9°，β1=－ 11.6°，γ1=－27.3°，T1=［3，3，10］；

第 2 幅图:α1=26.8°，β1=－ 8.6°，γ1=－38.5°，T1=［2，2，10］；

第 3 幅图:α1=28.3°，β1=－ 19.9°，γ1=40.1°，T1=［1，2，10］.

根据上述参数产生3幅图像，图像分辨率是2048×2048.在投影图像中，加入均值为0，标准偏差是步进为0.1像素从0到1变化的高斯噪声.在每个噪声水平下计算200次，得到的最终内参均值结果如表1所示.

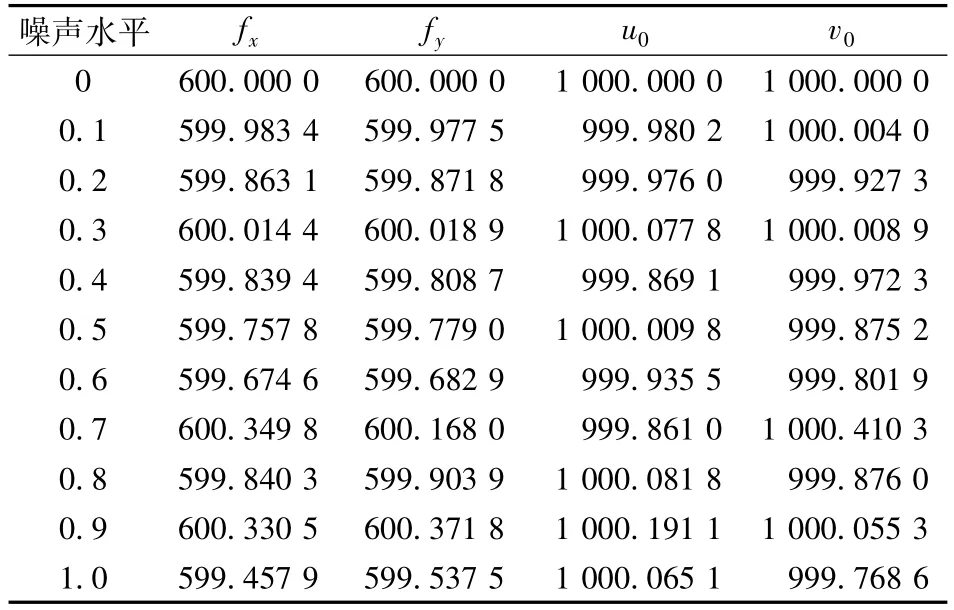
表1 不同噪声水平下内参的变化

从表1可以看出，内参的偏差在1以内.总体来说噪声对结果的影响都比较小，所以算法稳定，表1保存的结果是200次运算的均值结果，因为均值作用部分消除了噪声对结果的影响.本文利用均值方法来降低噪声对结果的影响，对仿真和实物实验进行了比较总结.因为篇幅有限，没有给出单次噪声的所有结果，fx和α在噪声为1像素时分别为607.4033 和17.3919.没有均值的结果比均值的差了1%左右，虽然这只是一个偶然的结果，但是说明了均值后的鲁棒性更强.

2.2 实物实验

所用摄像机为UNIQ UP-1800，分辨率为1380×1030像素.归一化后本文的重投影偏差是0.74587像素.拍摄的实物图如图4所示.

极坐标图像之间的相互关系简单，可以很方便地用于多摄像机标定，即可以预先做好标定板，如图3已经知道各自之间的相互关系，也可以在拍摄完图像之后再确定彼此的关系，这样就可以根据摄像机所在位置来决定极坐标图像的摆放位置.根据图4获得的摄像机参数，然后反求平面板的空间交汇效果图，如图5所示.

图4 实物图:极坐标标定板

图5 极坐标标定得到的平面空间交汇图

本文方法水平和竖直方向的平均距离差为2.648 cm，文献［1］对应的距离差为 2.553 cm，采用本文方法所得平面恢复的情况和采用文献［1］的方法所得结果基本一致.

图5是双目摄像机恢复的平面空间交汇图.

3 结语

本文提出了采用极坐标表示的图像完成了摄像机的标定，在多摄像机标定上的优势可以根据摄像机位置来布置极坐标图像，这样可以很方便地完成标定而不带来矩阵转移的累计误差.本文提出基于极坐标的平面图像来识别特征点，最后采用平面模板法完成标定；多摄像机标定采用统一世界坐标法，得到了较为准确的标定结果，并用简易的交汇验证了准确性.

References)

［1］Zhang Z.A flexible new technique for camera calibration［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(11):1330-1334.

［2］Tsai R.A versatile camera calibration technique for high-accuracy 3D machine vision metrology using offthe-shelf TV cameras and lenses［J］.IEEE Journal of Robotics and Automation，1987，3(4):323-344.

［3］Hartley R I.In defense of the eight-point algorithm［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19(6):580-593.

［4］Chaperon T，Droulez J，Thibault G.Reliable camera pose and calibration from a small set of point and line correspondences:a probabilistic approach［J］.Computer Vision and Image Understanding，2011，115(5):576-585.

［5］杨剑，杨秋翔，秦品乐.二维柔性拼接标定方法［J］.光学精密工程，2011，19(5):1134-1142.Yang Jian，Yang Qiuxiang，Qin Pinle.Two-dimensional flexible target for calibrating camera［J］.Optics and Precision Engineering，2011，19(5):1134-1142.(in Chinese)

［6］Liu Y H，Jia Q X，Sun H X，et al.Multi-camera calibration based on coplanar projection of points［C］//Proceedings of Computer Design and Applications(ICCDA).Qinhuangdao，China，2010(1):221-224.

［7］Kojima Y，Fujii T，Tanimoto M.New multiple-camera calibration method for a large number of cameras［C］//Proceedings of SPIE-IS＆T Electronic Imaging.San Jose，USA，2005，5665:156-163.

［8］Wang L，Wu F C，Hu Z Y.Multi-camera calibration with one-dimensionalobjectundergeneralmotions［C］//Proceedings of Computer Vision.Rio de Janeiro，Brazil，2007:1-7.

［9］王亮，吴福朝.基于一维标定物的多摄像机标定［J］.自动化学报，2007，33(03):225-231.Wang Liang，Wu Fuchao.Multi-camera calibration based on 1D calibration object［J］.Acta Automatica Sinica，2007，33(03):225-231.(in Chinese)

［10］Loaiza M E，Raposo A B，Gattass M.Multi-camera calibration based on an invariant pattern［J］.Computers ＆Graphics，2011，35(2):198-207.

［11］张广军，魏振忠.多视觉检测系统的世界坐标唯一全局标定方法［J］.北京航空航天大学学报，2006，32(11):1268-1272.Zhang Guangjun，Wei Zhenzhong.Unique world coordinates based global calibration method for multi-vision inspection system［J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32(11):1268-1272.

［12］Li Q，Da F P，Huang H M.An Improved Method of Location of the circular target［C］//Proceedings of Computational Aspects of Social Networks(CASoN).Taiyuan，China，2010:251-254.

［13］李勤，达飞鹏，温晴川.任意方向下的摄像机镜头畸变标定［J］.仪器仪表学报，2010，31(9):2022-2027.Li Qin，Da Feipeng，Wen Qingchuan.Calibrating lens distortion of camera in all directions［J］.Chinese Journal of Scientific Instrument，2010，31(9):2022-2027.(in Chinese)

［14］Ueshiba T，Tomita F.Plane-based calibration algorithm for multi-camera systems via factorization of homography matrices［C］//Proceedings of Computer Vision.Nice，France，2003:966-973.