武器-目标分配问题的分布估计算法及参数设计

高 尚

(江苏科技大学计算机科学与工程学院，镇江 212003)

武器-目标分配(weapon target assignment)问题是现代战争中十分重要的问题.Lloyd［1］等指出武器-目标分配问题是一个NP完全问题.为解决这个问题，人们提出了许多算法.Wacholker［2］提出了一种神经网络的解法，其依据Hopfield和Tank的神经网络模型，用此网络解WTA问题，此方法有时得不到稳定解；文献［3-4］对神经网络模型提出了改进算法；文献［5］用遗传方法解决了WTA问题；文献［6-7］用蚁群算法解决了WTA问题；文献［8］用粒子群优化算法解决了WTA问题；文献［9］用免役算法解决了WTA问题.各种算法各有优劣，本文用分布估计算法来解决WTA问题.

1 WTA问题

有 n个目标 T1，T2，…，Tn，迎击武器分布于 m个武器平台 W1，W2，…，Wm，第 i(i=1，2，…，m)个武器平台最多可使用ri个武器，对目标Tj最多可使用sj个武器，武器平台Wi迎击目标Tj的概率为pij(i=1，2，…，m；j=1，2，…，n)，武器最佳分配以分配迎击武器迎击全部目标的失败概率最小为目标.

若分配了武器平台Wi迎击目标Tj，则xij=1，否则xij=0.WTA问题的数学模型为

只有当 ri=1(i=1，2，…，m)，sj=1(j=1，2，…，n)时，上述问题为可转化为指派问题，可以用匈牙利法解［6］.对于一般优化问题实质是非线性0-1整数规划问题，属于NP-难题，目前没有有效的算法解此问题.

2 基本分布估计算法

分布估计算法的概念最初在1996年被提出［10-11］，分布估计算法提出了一种全新的进化模式.在传统的遗传算法中，用种群表示优化问题的一组候选解，种群中的每个个体都有相应的适应值，然后进行选择、交叉和变异等模拟自然进化的操作，反复进行，对问题进行求解.而在分布估计算法中，没有传统的交叉、变异等遗传操作，取而代之的是概率模型的学习和采样.分布估计算法通过一个概率模型描述候选解在空间的分布，采用统计学习手段从群体宏观的角度建立一个描述解分布的概率模型，然后对概率模型随机采样产生新的种群，如此反复进行，实现种群的进化，直到终止条件.根据概率模型的复杂程度以及不同的采样方法，分布估计算法发展了很多不同的具体实现方法，可以归纳为下面2个主要步骤［12-13］:首先构建描述解空间的概率模型，通过对种群的评估，选择优秀的个体集合，然后采用统计学习等手段构造一个描述当前解集的概率模型；然后由概率模型随机采样产生新的种群，一般地，采用蒙特卡罗方法，对概率模型采样得到新的种群.

遗传算法中的交叉和变异会破坏已经优化好的个体，分布估计算法用建立概率模型和采样两大操作取代了遗传算法中的交叉算子和变异算子，以一种带有“全局操控”性的操作模式解决了遗传算法存在的这一问题.遗传算法和分布估计算法的流程图对比如图1所示.并且分布估计算法不需要太多的参数设置，编程比遗传算法简单.

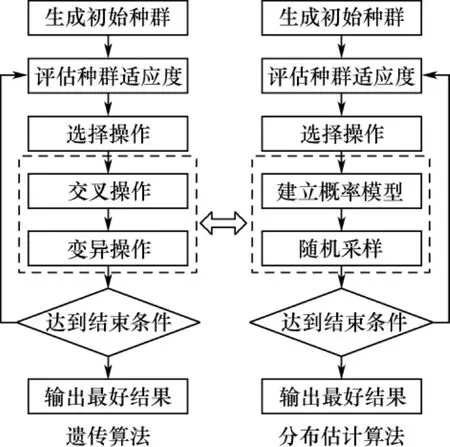
图1 分布估计算法与遗传算法的流程异同点

3 解武器-目标分配问题的改进分布估计算法

首先把原约束方程作为罚函数项加入到原目标中，变成无约束的优化问题，即

式中，M1，M2为一充分大的正数.这里提出用分布估计算法来解决此问题.

解武器-目标分配问题的分布估计算法如下:

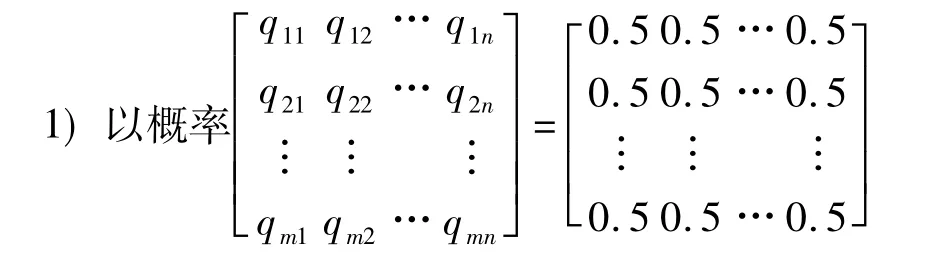
随机产生N个(取1的概率为0.5)个体组成一个初始种群；

2)评估初始种群中所有个体的适应度，保留最好解；

3)按适应度从高到低的顺序对种群进行排序，并从中选出最优的m个个体(m≤N)；

4)分析产生的m个个体所包含的信息，估计

采样，得到N个新样本，构成新种群；

6)若达到算法的终止条件则结束(如达到规定迭代次数nmax)，否则执行第2)步.

该分布估计算法的时间复杂性估算如下:以计算适应度操作花费最多，所以时间复杂性大约为O(Nnmax).

4 算法测试及参数设计

问题 1［6］有 6 个目标 T1，T2，…，T6，迎击武器分布于 4 个武器平台 W1，W2，W3，W4，每个武器平台最多可使用武器为(2，1，2，1)，对每个目标最多可使用1个武器，武器平台Wi迎击目标Tj的概率为 pij(i=1，2，…，4；j=1，2，…，6)，如表1 所示.

表1 m=4，n=6情况迎击概率表

问题 2［7］有 12 个目标 T1，T2，…，T12，迎击武器分布于5个武器平台W1，W2，…，W5，每个武器平台最多可使用武器为(3，3，3，3，3)，对每个目标最多可使用1个武器，武器平台Wi迎击目标Tj的概率为 pij(i=1，2，…，5；j=1，2，…，12)，如表2 所示.

表2 m=5，n=12情况迎击概率表

采用分布估计算法，当N=800，m=0.3N时，最好值的迭代过程如图2所示.问题1的最优解“武器1迎击目标4和目标6，武器2迎击目标2，武器3迎击目标1和目标3，武器4迎击目标5”，或“武器1迎击目标3和目标4，武器2迎击目标2，武器3迎击目标1和目标5，武器4迎击目标6”迎击全部目标的失败概率为1.4.

问题2的最优解“武器1迎击目标1和目标2，武器2迎击目标6和目标7，武器3迎击目标4、目标9和目标11，武器4迎击目标8、目标10和目标12，武器5迎击目标3和目标5”，迎击全部目标的失败概率为2.9(比文献［7］结果好)，最好值的迭代过程如图3所示.

图2 解问题1的迭代过程

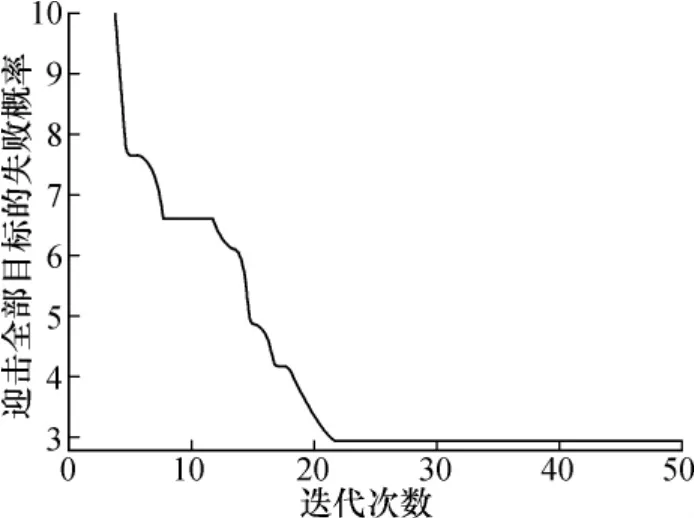
图3 解问题2的迭代过程

影响分布估计算法性能的主要参数是种群的个数N和选出的种群个数m.N取不同值，m=0.3N，解问题1和问题2，各种算法各测试100次，统计数据如表3所示.从表3可知，N越小，样本数量不足，效果不好；N越大，效果越好，当然需要的时间也越大.因此N取适中即可，如N取800.

当N=800时，选出的种群个数m占N的比例不同，结果也不一样.不同的比例，解问题1和问题2，算法各测试100次，统计数据如表4所示.从表4可以看出，m/N比例越大，不能体现出选优的优势，效果越不好；当然m/N比例太小，也容易陷入局部极值.因此m/N比值取30%左右，效果比较好.

5 结语

本文的分布估计算法不仅可以解决WTA优化问题，为研究WTA问题提供一种新的思路.对于整数规划问题，对该算法作适当修改，也可适用.分布估计算法研究处于初期，还有许多问题值得研究，如算法的收敛性、理论依据等.但从当前的分布估计算法的应用效果来看，这种新型的寻优思想无疑具有十分光明的前景，更深入的工作还有待于进一步展开.

表3 N取不同值结果比较

表4 m/N取不同值结果比较

References)

［1］Lloyd S P，Witsenhausen H S.Weapons allocation is NP-complete［C］//Proceedings of the IEEE Summer Simulation Conference.Reno，NV，USA，1986:1054-1058.

［2］Wacholder E.A neural network-based optimization algorithm for the static weapon-target assignment problem［J］.ORSA Journal on Computing，1989，1(4):232-246.

［3］Ressler J L，Augusteijn M F.Weapon target assignment accessibility using neural networks［C］//Proceedings of the 1992 Artificial Neural Networks in Engineering.St.Louis，MO，USA，1992:397-402.

［4］朱齐丹，胡绍勇，宋福香，等.解武器-目标分配问题的神经网络方法［J］.哈尔滨工程大学学报，1997，18(3):36-41.Zhu Qidan，Hu Shaoyong，Song Fuxiang，et al.A neural network algorithm of solving weapon-target assignment problem［J］.Journal of Harbin Engineering University，1997，18(3):36-41.(in Chinese)

［5］曹奇英，何张兵.WTA问题的遗传算法研究［J］.控制理论与应用，2001，18(1):76-79.Cao Qiying，He Zhangbin.A genetic algorithm of solving WTA problem ［J］.Control Theory and Applications，2001，18(1):76-79.(in Chinese)

［6］高尚.武器-目标分配问题的蚁群算法［J］.计算机工程与应用，2003，39(3):78-79.Gao Shang.Ant colony algorithm for weapon-target assignment problem［J］.Computer Engineering and Applications，2003，39(3):78-79.(in Chinese)

［7］黄树采，李为民.目标分配问题的蚁群算法研究［J］.系统工程与电子技术，2005，27(1):79-80；130.Huang Shucai，Li Weimin.Research of ant colony algorithm for solving target assignment problem［J］.Systems Engineering and Electronics，2005，27(1):79-80；130.(in Chinese)

［8］高尚，杨静宇.武器-目标分配问题的粒子群优化算法［J］.系统工程与电子技术:2005，27(7):1250-1252；1259.Gao Shang，Yang Jingyu.Solving weapon-target assignment problem by particle swarm optimization algorithm［J］.Systems Engineering and Electronics，2005，27(7):1250-1252；1259.(in Chinese)

［9］Lee Z J，Lee C Y，Su，S F.An immunity-based ant colony optimization algorithm for solving weapon-target assignment problem［J］.Applied Soft Computing Journal，2002，2(1):39-47.

［10］周树德，孙增圻.分布估计算法综述［J］.自动化学报，2007，33(2):113-124.Zhou Shude，Sun Zengqi.A survey on estimation of distribution algorithms［J］.Acta Automatica Sinica，2007，33(2):113-124.(in Chinese)

［11］Muhliebe H，Paass G.From recombination of genes to the estimation of distributions I.binary parameters［C］//Lecture notes in computer science.Springer Verlag，1996，1141:178-187.

［12］Pelikan M，Godberg D E，Cantu-Paz E.Linkage problem，distribution estimation，and Bayesian networks［J］.Evolutionary Computation，2000，8(3):311-340.

［13］Paul T K，Iba H.Linear and combinatorial optimizations by estimation of distribution algorithms［C］//9th MPS Symposium on Evolutionary Computation.Information Processing Society of Japan(IPSJ)，2002:99-106.