复方药物剂量配比多目标优化的方法学研究*

盖玉权 ，何 昱 ，张宇燕 ，吴宪彬 ，万海同

（1.浙江中医药大学，浙江 杭州 310053；2.浙江万里学院，浙江 宁波 315101）

实际优化问题大多数是多目标优化问题MOP（Multi-Objective optimization Problems），多目标优化问题最主要的特点是目标间的矛盾性和不可共度性，即一个目标的改善可能会使得另一个目标值变劣，目标间一般没有统一的度量标准，因而不能直接比较[1]。多目标问题的最优解是一组最优解的集合，称为非劣解集，即Pareto解集。

药物研究中的许多问题都是多目标优化问题。例如，在药物的药效评价研究中，如何确定最佳方案，以使各治疗效应目标都处于较好水平并且副作用相对最小等。这样的多目标评价问题在中药制剂、生产工艺、药理和药效中比比皆是。在中药复方药物的研究中，中药复方的量效关系具有非线性特征，不同剂量的组方药效可能存在着差异，且中药药效具有多途径、多靶点特征[2]，选取不同的药效指标及指标权重，复方组分配比及组分间相互作用机制也不同，因而有必要寻找能够提升复方疗效、使多个药效指标达到综合最优的药味剂量。本研究以苓桂术甘汤为例，采用遗传算法优化支持向量机建立量效关系多目标优化模型，基于非支配排序遗传算法进行模型求解，得出一组分配均匀的Paeto解，熵权法结合专家经验确定指标组合权重，依据逼近于理想解的多属性决策技术（TOPSIS）对 Pareto方案排序并择优。

1 算法简介

1.1 支持向量机

中药复方量效关系是一个非线性、确定的多变量输入输出关联系统，涉及到的动力学过程极为复杂，很难用确定的数学模型来描述。配比的多目标优化需要有可靠的、能够反映各参数变化规律及相互作用关系的数学模型。支持向量机SVM（Support Vector Machine）理论是一种专门研究有限样本预测的学习方法，具有严格的理论和数学基础，是一种新型的结构化学习方法。它能很好地解决有限数量样本的高维模型构造问题，小样本学习使它具有很强的泛化能力，且SVM算法是一个凸优化问题，因此局部最优解一定是全局最优解。其原理为：对 于 给 定 的 样 本 集{（xi，yi）|i=1，2， … ，k}， 其 中 xi为 输入向量，yi为期望输出，寻求一个样本的最优函数关系y=f（x），采用适当的核函数 K（xi，x）确定回归模型[3]。

1.2 非支配排序遗传算法

非支配排序遗传算法NSGA-II（Nondominated Sorting Genetic Algorithm）是带精英策略的非支配排序遗传算法，它是Deb等人在NSGA的基础上加入快速非支配排序算法、引入精英策略、采用拥挤度和拥挤度比较算子发展起来的，是一种基于Pareto最优概念的遗传算法，是众多的多目标优化算法中体现Goldberg思想最直接的方法[4]。传统多目标优化方法将多目标问题转化为单目标问题，如综合评分法、综合平衡法、线性加权法等，此类方法只能找出一个Pareto最优解，且需要较多的专家经验，而NSGA-II算法可以求出一组分布均匀的Pareto最优解集，用来逼近多目标优化问题的所有Pareto最优解，为决策者提供了较多的备选方案。

1.3 熵权Topsis法

熵是热力学中重要概念，是物质系统无序状态的量度，系统越乱，熵就越大，系统越有序，熵就越小。将熵的概念引入信息论，则表示一个信息源发出的信号状态的不确定程度[5]。中药复方剂量配比研究中，以往决策模型大部分只考虑决策者（专家）的主观判断权重，没有体现决策目标拥有的决策信息。本研究采用熵值来度量所获得决策信息，将主观权重与复方量效关系的客观情况相结合，依据TOPSIS法求解最佳配比方案。步骤[6]如下：

（1）构建判断矩阵：R′=（r′ij）m×n；

（2）模糊数学规范化判断矩阵：R=（rij）m×n；

（6）构造结合组合权判断矩阵；

（7）求理想解和负理想解：xj+和 xj-；

（10）将 Sj从大到小排列，Sj大者为优。

2 仿真实例

2.1 数据来源[7]

仿真数据如表1所示，其中利尿和抗缺氧为越大越好型指标，抗室颤效果是以室颤率为测量指标，故为越小越好型指标。

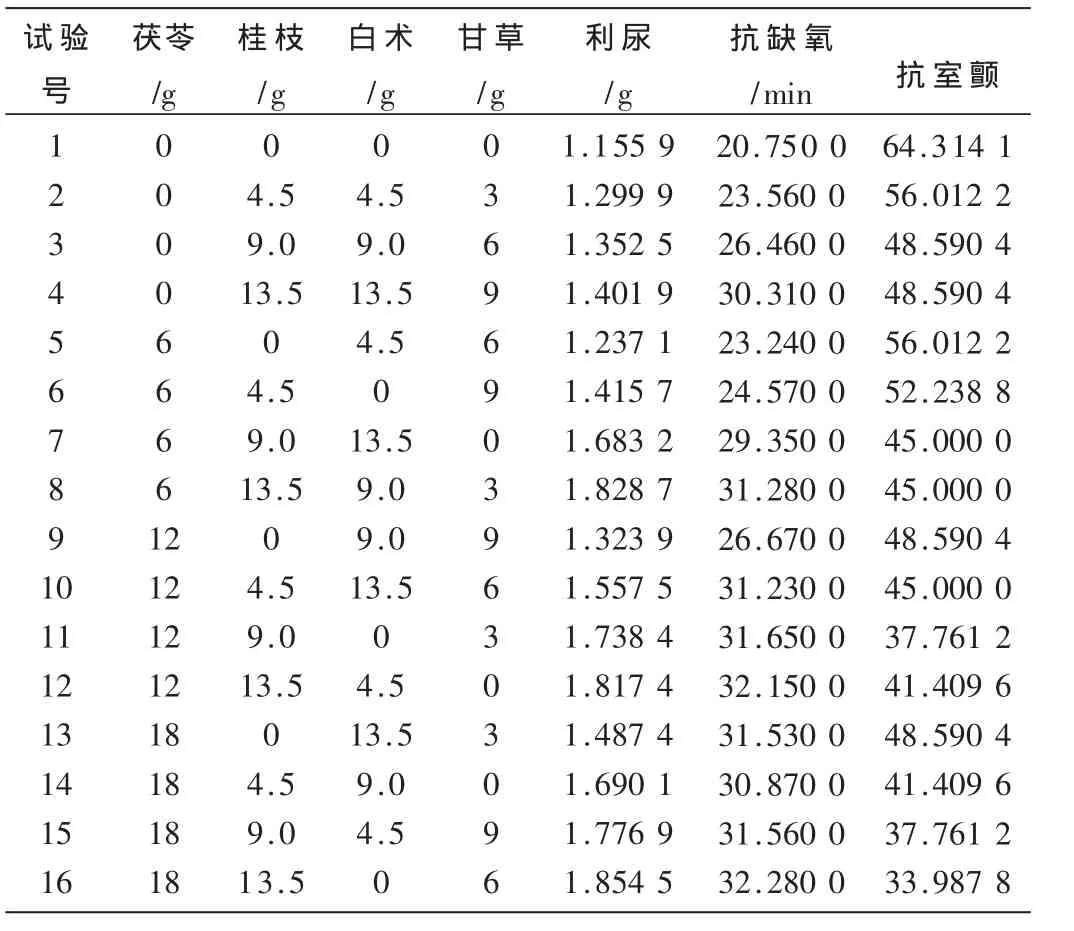
表1 苓桂术甘汤药理实验及其结果

2.2 支持向量机建模

选取苓桂术甘汤正交设计各配伍组为输入，分别以利尿、抗缺氧和抗室颤为输出，建立量效关系SVM模型。为了提高SVM方法的预测精度，需要选择合适的核函数以及合适的相关参数值。由于在没有先验知识指导的情况下，用径向基函数往往能够得到较好的拟合结果[8]，故本文采用径向基核函数并基于遗传算法[9]优选-c和-g参数，以拟合相关系数和预测相对误差为指标建立量效关系支持向量机模型，前14组实验用来训练模型，第15、16组数据检测算法性能。

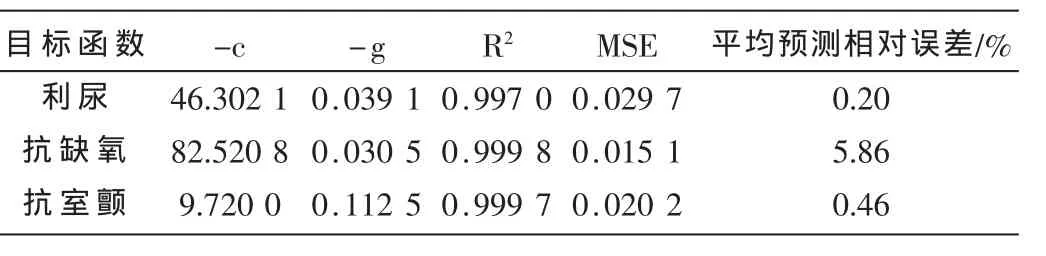
表2 支持向量机参数寻优结果

由表2可知，所建SVM模型对数据具有良好的拟合效果和预测效果，可用于多目标优化Pareto方案的求解。分别控制其他药味剂量为原方水平考察茯苓、桂枝、白术和甘草对利尿、抗缺氧和抗室颤三药效指标的影响，结果如图1所示。

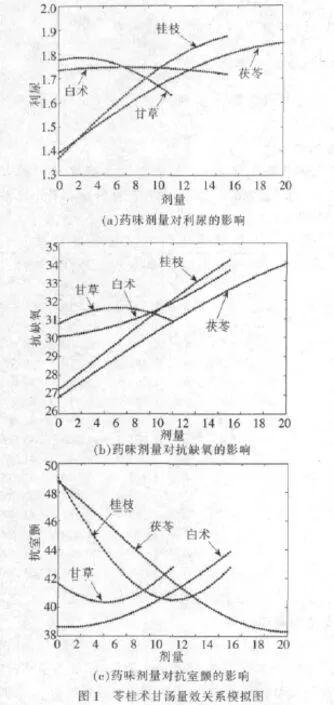
由图1可知，苓桂术甘汤各药味剂量大小对药效起着决定性的影响，在一定剂量范围内，主药桂枝和茯苓对三药效指标作用强烈，随着剂量的增加药效增强幅度变缓，低于原方剂量时主药量效关系接近线性，而白术和甘草对药效指标的直接作用效果不明显。

2.3 单目标遗传算法搜索理想解

构造三药效指标的目标函数，采用二进制编码，初始种群100，最大遗传代数为50代，变量二进制位数20， 代沟 0.9， 选择随机遍历抽样 （sus）， 单点交叉（xovsp）概率为 0.7，利用 gatbx工具箱编程，分别寻找三目标最佳值及对应药味剂量，程序运行结果如表3所示。

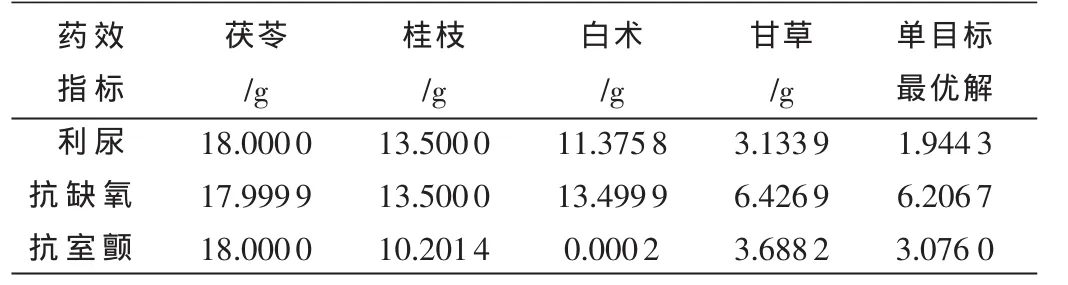
表3 三目标最佳值及对应药味剂量

由表3可知，三目标各自的最优解均高于正交试验所得结果，且最佳剂量配比不尽相同，即不存在使三目标同时达到最佳配比的方案。

2.4 NSGA-II算法进行多目标优化

采用实数编码，初始种群大小为200，小生境锦标赛选择，模拟二进制交叉和变异，最大遗传代数为50代。应用Matlab进行编程，由NSGA-II算法得到的三目标Pareto前沿如图2所示。

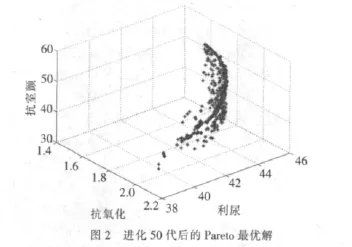
由图2可以看出，当种群进化到50代时，所得的Pareto最优解具有良好的多样性。这些解在不同的目标上各占优势，决策者可以根据不同的偏好，在这些解折中直接选择，但直接选择法具有较强的主观随意性。研究者还可对优化参数进行限定并修改算法中的一些条件进而使算法使用范围得到拓展，例如可将搜索范围设置在药效增加较快的水平等。

2.5 熵权TOPSIS法进行Pareto方案排序

在多目标优化获得一组Pareto解后，还需要对解集决策以挑选出基于方案的最优解。在Pareto最优解集基础上构造决策矩阵，决策属性定义为所考虑的3个目标函数，因此决策矩阵的大小为500×3。依据熵权法计算各指标熵值分别为0.989 7、0.992 5和0.941 3，熵权分别为 0.135 2、0.097 4和 0.767 3，说明抗室颤指标在Pareto方案中所含信息量最大，是影响最佳配比选择的主要因素。主观权重可由研究者根据临床经验及病人个体化差异确定，本研究将因子分析法[10]确定的三指标权重作为主观权重，分别为 0.332 8、0.331 3、0.335 9。按照TOPSIS方法对Pareto解进行排序，表4给出了贴近度从大到小的前10个方案。

以贴近度最大的方案为最终的优化解，得到：茯苓=16.974 8 g，桂枝=11.890 9 g，白术=12.081 4 g，甘草=1.370 4 g。

3 讨论

3.1 支持向量机参数的选择

SVM和大多数机器学习算法一样，其性能的优劣与参数和特征的选择有关。不同的参数优化方法其拟合和预测效果有一定的差异。常用的参数优化方法有网格搜索法[11]、粒子群优化算法和遗传算法[12-13]。本研究分别比较了三种参数优化方法，研究表明，网格搜索作为一种非启发式搜索，运算量较大，粒子群算法开始寻优迅速，但容易陷入局部最小，而遗传算法寻优速度逐渐变快，并且没有陷入局部最小，可有效实现参数寻优。

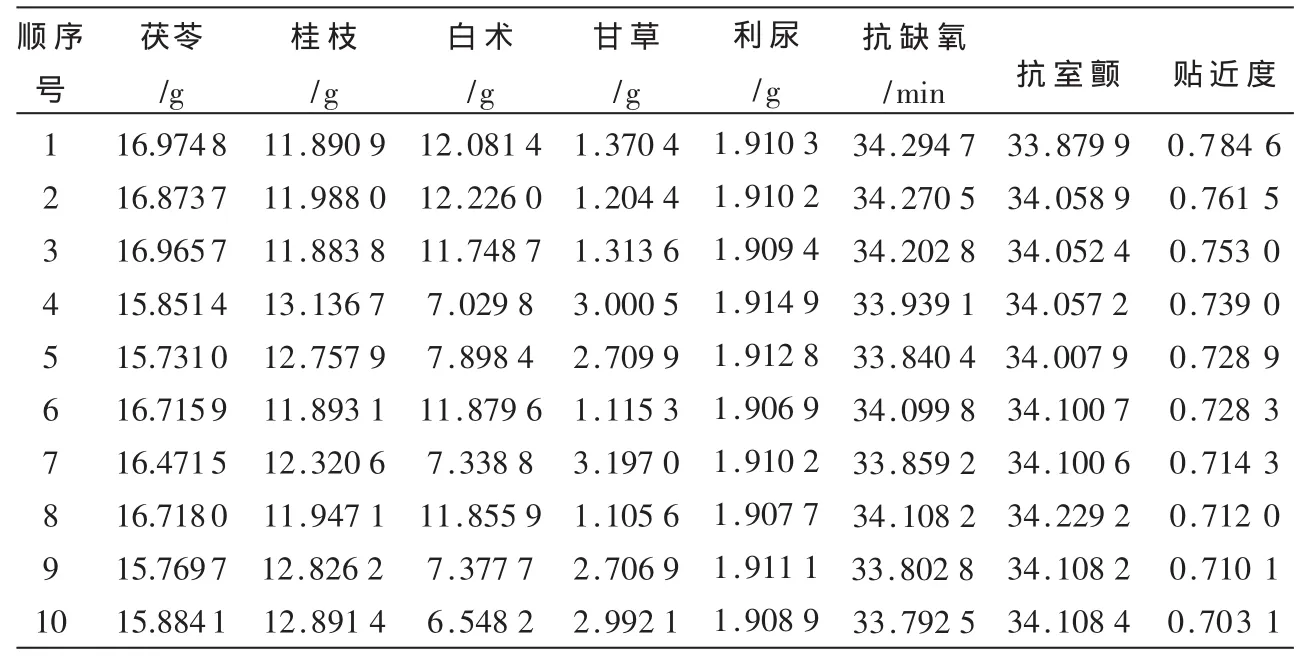
表4 排序前十位的Pareto方案及其贴近度

3.2 采用组合权重的优点

熵权并不是在决策问题中某指标实际意义上的重要性系数，而是在给定被评价方案集后各种评价指标值确定的情况下，各指标在竞争意义上的相对激烈程度系数，只代表该指标在该问题中提供有用信息量的多寡程度。单纯采用熵权计算权重，属性权重只能反映数据本身的特点，不能代表属性的重要程度[14]。本文利用客观熵权结合主观专家权重的方法进行组合赋权，可以有效地避免传统方法中权重系数确定过程的主观色彩，同时更注重了评价体系指标本身的重要程度，充分利用了被评判指标的信息量，综合权重既可以反映客观的决策信息，又可以体现决策者对决策指标的偏好，因而使决策结果具有更高的准确性和实用性。

3.3 复方标准剂量的确定

本研究中确定的苓桂术甘汤剂量不能作为标准剂量，由表3可知，当选取的药效指标不同时，其最佳剂量也不同。即使选择相同的药效指标，研究者还应根据病人的个体化差异灵活确定不同的主观权重，进而从Pareto方案中择优。因此，复方最佳剂量的确定应结合不同的药效指标及临床经验共同确定。

3.4 存在问题及解决办法

由图1可知，在一定范围内，药效指标随着苓桂术甘汤各药味剂量的增加改善不明显，即投入的剂量并未转化为理想的药效输出。后续工作将采用数据包络分析DEA（Data Envelopment Analysis）[15-16]，即将复方量效关系视为一个投入产出系统，药效指标的改善视为复方各药味剂量投人转化后的直接和间接产出，产出的多少不仅依赖于投入（药味剂量）的多少，还依赖于投入产出的效率。拟采用基于投入的C2R模型以决策单元DMU（Decision Making Units）的效率评价指数 θ、投入产出冗余松弛变量 s+及s-进行量效关系评价，计算投入产出比（研究结果将另文发表）。

支持向量机作为一种专门研究小样本情况下机器学习规律的理论，比传统的统计学习理论和神经网络具有更好的泛化推广能力，能够很好地解决中药复方量效关系非线性建模问题。非支配排序遗传化算法作为一种模拟自然进化过程的随机优化方法，同时也是一种全局性概率优化方法，用于多目标优化不仅可以一次性获得大量Pareto最优解，而且其优化结果具有良好的一致性。熵权TOPSIS法可在某种程度上反映决策指标含有的信息的多少，充分表现不同配比之间的指标差异，避免了决策过程的主观性和盲目性。支持向量机建模、非支配排序遗传算法多目标优化、熵权TOPSIS多属性决策三者结合可较好解决复方剂量配比多目标优化问题。

参考资料

[1]张志刚，马光文.基于NSGA-II算法的多目标水火电站群优化调度模型研究[J].水力发电学报，2010，29（1）：215-216.

[2]田景振，王厚伟.基于中药方剂的中药多维组合药物研究模式探讨[J].山东中医药大学学报，2011，35（2）：99-101.

[3]范玉妹，郭春静.支持向量机算法的研究及其实现[J].河北工程大学学报：自然科学版，2010，27（4）：106-112.

[4]HERIS S M，KHALOOZADEHH.Open-and closed-loop multiobjective optimalstrategiesforHIV therapy using NSGA-II.[J]. IEEE Transaction Biomed Engineering，2011，58（6）：1678-1685.

[5]刘晓，张宇.基于熵权和层次分析法的宿舍综合评价[J].科学技术与程，2011，11（2）：304-307.

[6]王国全，冯光文.熵权TOPSIS法在优选低放射性装饰建筑材料中的应用[J].环境科学与管理，2011，36（1）：22-25.

[7]宋宗华，冯东.苓桂术甘汤配伍机制及药效物质基础研究[J].中成药，2003，25（2）：133-138.

[8]LIN H T，LIN C J.A study on sigmoid kemels for SVM and the training of non-PSD kemels by SMO-type methods[EB]，2003.

[9]刘璐，刘爱伦.基于改进的遗传算法优化支持向量机的精馏塔故障诊断[J].华东理工大学学报：自然科学版，2011，37（2）：228-233.

[10]何君，石城，杨思波，等.基于因子分析和 AHP的水资源可持续利用综合评价方法 [J].南水北调与水利科技，2011，9（1）：75-79.

[11]张向东，冯胜洋，王长江.基于网格搜索的支持向量机砂土液化预测模型 [J].应用力学学报，2011，28（1）：24-28.

[12]高昆仑，刘建明，徐茹枝.基于支持向量机和粒子群算法的信息网络安全态势复合预测模型[J].电网技术，2011，35（4）：176-182.

[13]武海巍，于海业，张蕾.基于参数优化支持向量机的林下参净光合速率预测模型 [J].光谱学与光谱分析，2011，31（5）：1414-1418.

[14]王国全，冯光文.熵权TOPSIS法在优选低放射性装饰建筑材料中的应用[J].环境科学与管理，2011，36（1）：22-25.

[15]张鹏，秦毓毅，唐茂林，等.基于数据包络分析的水电企业节能调度效益评价 [J].四川电力技术，2011，34（2）：91-94.

[16]MOUSAVI A S， RAFIEE S， JAFARI A， et al.Improving energy productivity ofsunflowerproduction using data envelopment analysis （DEA）approach[J].J Sci Food Agric，2011，91（10）：1885-1892.