高级加密标准算法R i j n d a e l的分析与应用*
张青凤 ,张凤琴 ,王 蓉
(1.运城学院,公共计算机教学部,山西 运城 044000;2.空军工程大学,计算机系,陕西 西安 710077)
1 Rijndael算法的背景
AES(Advanced Encryption Standard)是美国联邦标准局于1997年开始向全世界征集的加密标准[1],属于对称加密算法,代表了当今最先进的编码技术,最终获胜的是RijnDael算法。统计显示,即使使用目前世界上运算速度最快的计算机,穷尽128 bit密钥也需要几十亿年的时间,更不用说去破解采用256 bit密钥长度的AES算法了。
Rijndael算法由比利时计算机科学家Vincent Rijmen和 Joan Daemen 开发, 它使用 128 bit、192 bit、256 bit的密钥长度,比 56 bit的 DES更健壮可靠[3]。美国国家标准技术研究所选择Rijndael作为美国政府加密标准AES的加密算法,取代早期的数据加密标准DES[1]。Rijndael作为一种迭代分组加密算法,其数据块长度和密钥长度均是可变的,因此它汇聚了强安全性、高性能、高效率、易用、灵活等优点被广泛应用在各个领域中。
2 Rijndael算法的设计原理
Rijndael作为加密标准AES算法,其128 bit输入分组用以字节为单位的矩阵方阵描述[4]。该数组被复制到State数组。数据块长度、密钥长度可以被设定为128 bit、192 bit、256 bit三个可选长度,相应的加密轮数分别为10、12、14,每一轮循环都有一个循环密钥,它来自于初始密钥。
2.1 Rijndael算法的加密流程
加密过程分为四个阶段:密钥扩展、轮密钥加、Nr-1(128 bit、192 bit、256 bit密钥长度,Nr分别为 10、12、14)轮变换及最后一轮变换。轮变换包括字节代换、行移位、列混淆和轮密钥加四个过程,最后一轮变换包括字节代换、行移位和轮密钥加三个过程。其流程图如图1所示。
(1)状态:指明文分组及每次变换的中间结果[4],是一个4×Nb的矩阵,Nb为数据块长度除以32。
(2)字符代换:用一个简单的查表操作代替了基于矩阵乘法的复杂仿射变换。S盒是一个16×16字节矩阵,包含8 bit值所能表达的256种可能的变换。把Statc中每个字节的高4位作为行值,低4位作为列值,取出S盒中对应行列的元素作为新的字节输出。

图1 Rijndael算法加密流程
(3)行移位:State的第一行保持不变,第 2、3、4行分别循环左移1、2、3个字节。
(4)列混淆:可表示为基于系数矩阵CoefMix与State的矩阵乘法。乘积矩阵中的每个元素S[i,j]是系数矩阵中一行元素CoefMix[i,k]与State矩阵中对应一列元素State[k,j]的乘积之和。这里的加法与乘法都定义在有限域 GF(28)上:加法即按位“异或”操作,乘法遵循 GF(28)上的多项式乘法规则[2]。
(5)轮密钥加:是基于 State列的操作,即把 State一列中的4个字节与轮密钥RoundKey的1个字进行 “异或”。
(6)扩展密钥:以 4个字密钥为输入,生成 44字扩展密钥数组ω[44],为初始轮密钥加阶段和后面10轮变换提供轮密钥。输入密钥直接被复制到扩展密钥数组的前4个字,然后每次用4个字填充扩展密钥数组余下的部分[4]。 在扩展密钥数组中,ω[i]值依赖于 ω[i-1]和 ω[i-4]。 ω 数组中下标不是 4的倍数时,ω[i]为 ω[i-1]和ω[i-4]的“异或”。 下标为 4的倍数时,首先将 ω[i-1]的4个字节循环左移1个字节,然后利用S盒对每个字节进行字节代换,再与轮常量按位“异或”。轮常量是1个字,其最右边3个字节为0,最左边 1个字节的值 RC[j]与轮数 j相关。 RC[1]=1,RC[j]=2·RC[j-1],乘法定义在GF(28)上。RC[j]值以十六进制表示。
(7)加密轮数 Nr:在 Rijndael算法中,运算的轮数(Nr)是由Nb及Nk所决定的[4],轮数的变动定义如表1所示。
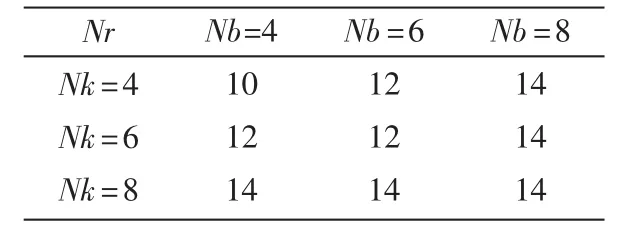
表1 Nr、Nb、Nk 关系
2.2 解密过程
Rijndael解密过程是加密的逆过程,每轮循环中的步骤都被它们的逆所替换,值得注意的是:循环密钥使用起来应该颠倒次序。
3 Rijndael算法的应用
Rijindael算法常被用于文件的加解密过程,加密时先将读入的明文依次分组,用加密密钥将明文加密后写入文件中;解密时用解密密钥将文件中的密文解密后将明文写入结果文件中。
3.1 Rijindael算法在文件加解密应用的实现

3.2 加密模块实现


3.3 解密模块的实现


Rijndael算法一直经受着世界各国密码机构和专家的攻击,最有名的当属 Squre攻击[4]。目前Rijndael算法已被广泛应用于身份认证、数字签名、数据加密等方面,由于硬件的加解密速度要比软件快,且可在物理上保证系统安全,国内很多单位用硬件的方法来实现该算法。
[1]段钢.加密与解密(第 3版)[M].北京:电子工业出版社,2008.
[2]冯登国.信息安全中的数学方法与技术[M].北京:清华大学出版社,2009.
[3]Http://zhidao.baidu.com.
[4]DAEMEN J,RIJMAN V.高级加密标准算法(AES)—Rijndael的设计[M].谷大武,徐胜波译.北京:清华大学出版社,2003.

