基于非负矩阵分解的城市公交网络综合评价模型

周媛

（西安外事学院 工学院，陕西 西安 710077）

城市公共交通系统是一个城市的重要基础设施，是城市经济发展和人们生活所必须的公益性事业，直接关系到城市整体功能的发挥、市民生活质量的提高和城市的可持续发展。

公共交通网络的综合评价就是在对公共交通网络经济效益、社会效益和环境效益及其技术性能等各部分、各阶段、各层次子系统评价的基础上，谋求规划系统整体功能的最优调节，并在系统整体优化过程中，不断向决策者提供各种关联信息[1-2]。

笔者所提出的基于非负矩阵分解的城市公交网络综合评价模型，可以有效地给出城市公交网络各项指标的量化权重，从而可以有效地避免评价结果无明确几何意义和评价结果主观依赖性等缺点。通过对银川市现有的公交网络进行综合评价后证实，笔者所提出的方法可以客观评价现有公共交通系统的整体状况，把握其总体发展水平，找出存在的问题及可能发挥的潜力，为城市公共交通的进一步发展提供规划、建设、管理等方面的依据，从而最大程度地发挥城市公共交通系统的最佳效益，对整个城市交通管理起到积极的推动作用。

1 城市公交网络的评价指标体系

1.1 评价指标体系建立原则

城市公交网络综合评价是辅助公交规划决策的一个必备手段，它为决策过程的各种参与者提供现实依据和度量准绳。同时该评价又是多目标、多层次、多因素的，因而评价指标体系的建立应遵循以下原则[3]：首先，评价指标体系应能够综合反映城市公交网络发展水平，并尽可能细致的反映其各个侧面的特征和状况；其次，评价指标的选择应尽量选取日常统计指标或容易获得的指标，且尽可能精简，以便直观、简明地说明问题；第三，评价指标权重的确定、数据的选取、计算与合成必须以公认的科学理论为依据；最后评价指标体系应具有横向及纵向的可比性，即便于对各城市公交网络在空间上和时间上进行综合比较研究。

1.2 城市公交网络综合评价指标体系

针对不同的评价目标和评价对象建立相应的评价指标体系是进行综合评价的基础。笔者所要评价的对象是城市公共交通网络，是一个较为宏观的评价对象，其涉及面广、内容多，因而评价指标选取考虑的因素也多，用简单的线性结构难以描述各指标的内在联系。故采用层次分析法建立树状的关系结构，运用目标层次分类展开法，将目标按逻辑分类向下展开为若干目标，再把各个目标分别向下展开成分目标或准则 （准则层），依次类推，直到可定量或可进行定性分析（指标层）为止。为了使所构造出的指标体系能更真实、完整、准确地评价一个城市公共交通网络的综合水平，通过反复对比、探讨和征询有关专家的意见，依据上述评价指标体系建立原则，结合我国城市公共交通网络的实际情况，提出了如图1所示的评价指标体系。

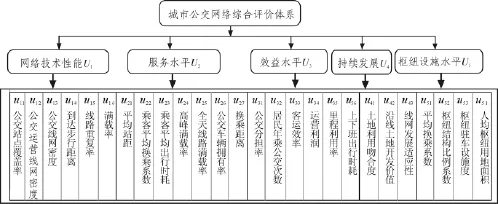
图1 城市公交网络综合评价体系Fig.1 Comprehensive evaluation model of public transit network

2 非负矩阵分解综合评价原理

在上一节中已经对公交系统的指标进行了提取，那么如何组合这些指标进而量化的评价一个公交系统就成了下面要解决的问题。非监督的学习算法近年来是一类主流的对数据矩阵进行分解的策略，例如主成分分析法（Principle Components Analysis，PCA）[3]就是这个领域内的一种传统的主流研究方法。但是PCA存在一个十分主要的问题，就是PCA法得到的特征向量并不能保证是非负的，也就是说非负系数对应的成分对于主成分的贡献是无法确定的。在这种情况下我们就无法有效的对各个子成分的有效性进行量化研究。而新兴的非负矩阵分解（Non-negative Matrix Factorization，NMF）[4]技术就有效地解决了上述问题。下面首先对非负矩阵分解的数学知识进行简单的介绍。

当给一个非负矩阵 Vm×n，NMF技术是寻找出矩阵 Wm×r和Hr×n满足式（1）所示的优化。

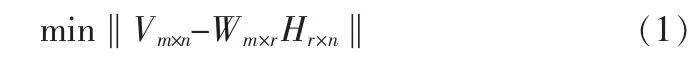
从式（1）中可以看出，NMF将会找到一组非负的分解因子W和H使其满足：

其中角标代表矩阵的维数，特别需要一提的是r的值就是代表着分解基的数量，也就是分解空间的维数。假设H=（β1，…，βn）此时式（2）可进一步改写为：

从式（3）的几何意义可以看出，这时矩阵W就代表是基矩阵，V矩阵的各列可以理解H矩阵经过矩阵W对其各列进行线性变换所得，从而H矩阵中的每一列βi便是所需的分解结果。NMF的最大的好处就是基矩阵W内的数值全都为正，从而极为方便我们量化的分析各个子成分的组合后的指标中所占的权重，极大地方便了对公交系统的量化评价以及有针对性的改进。

3 实例分析

银川市是宁夏回族自治区首府，是“乎-包-银-兰”经济带的中心城市。全市总面积9 170.3平方公里，建成区面积89.2平方公里，中期规划（2015年）市域户籍人口160万，流动人口25万。公交出行在居民非体力出行中所占比例最高，达17.42%，根据居民出行产生和分布预测，规划年银川市中心区公交出行量为125万人次/日。可见为银川规划、建设、管理提供科学依据就显得十分重要。现以银川市的现状公交网络为例，利用上述基于非负矩阵分解的评价方法对其进行综合评价。

Step1：确定分解矩阵V。

采取专家打分的策略获得各项指标的数值[5-6]，以下给出每个指标所在的区间，如表1所示。

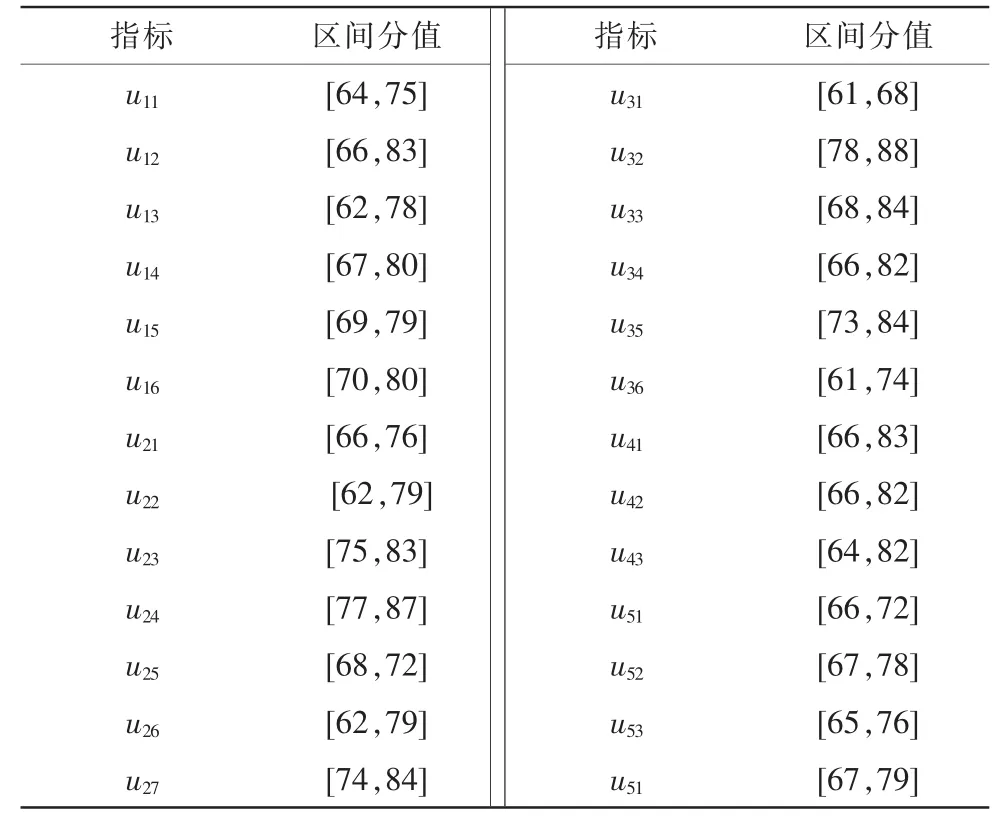
表1 各指标实际得分对应区间Tab.1 Corresponding intervals of each index

Step2：确定分解矩阵与基矩阵：

由于事先并无法确定主要成分的个数r，因此采取循环求取的方法，对r从1到26进行分别实验，然后从中选取近似程度最大且成分个数相对较少的r。实验结果表明当r=5或r=6为一个合理的选择。这一点也与之前将评价体系分为5个大类相吻合。下面以r=5进行计算，由非负矩阵分解得到的各项权系数在5个大项中进行求和得到，其各项的权系数分别为：

将其与银川市各项指标进行内积后我们得到银川市公交网络状况的总评价E为：

鉴于文中的评价结果，银川市在近期中期公交规划中需在以下几方面做出改进：1）优化公交线网总体布局，明确结构层次及功能；2）降低线路重复系数，提高线网覆盖率；3）合理规划公交场站用地；4）适当提高公交车配给水平，改善乘客乘车环境。逐渐形成干支协调、结构合理的多元化、高质量服务水平的公共交通系统[7]，为市民提供快速、安全、舒适、经济的客运交通服务。

4 结束语

笔者立足于我国交通和社会经济发展的形势与要求，结合国内外有关研究经验和发展趋势，在规划实践工作的基础上，从模型方法和系统方法的角度，研究城市公共客运交通网络评价的理论与方法，参阅大量相关文献，深入思考其中的思想方法内容，探索我国公共交通网络评价之路，具有理论和实践双重重要意义：

1）利用多层次多指标模糊综合评价方法，建立城市公共交通网络的多级评价模型，对城市公共交通网络评价中诸多因素进行分级分类的逐层评价，以定量的数值表示评定结果，从而能够客观、全面、清晰地反映城市公共交通网络发展的综合水平。

2）基于非负矩阵分解的城市公交网络综合评价模型可以克服传统PCA方法结果无明确几何意义和评价结果主观依赖性等缺点。试验结果表明该方法的评定结果具有明确的实际意义，在城市公共交通网络发展综合水平评价领域中具有良好的应用前景。

[1]王炜，杨新苗，陈学武.城市公共交通系统规划方法与管理技术[M].北京:科学出版社，2002.

[2]胡启洲，邓卫，张卫华.城市公交线网的灰色评价及其应用[J].交通运输系统工程与信息，2006（2）：58-61.HU Qi-zhou，DENG Wei，ZHANG Wei-hua.A grey-theorybased evaluation with application for urban public traffic network[J].Journal of Transportation Systems Engineering and Information Technology，2006（2）:58-61.

[3]Martinez A M，Kak A C.PCA versus LDA[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2001，23（2）:228-233.

[4]Lee D D，Seung H S.Learning the parts of objects by nonnegative matrix factorization[J].Nature，1999，401 （6755）:788-791.

[5]张兴芳，管恩瑞，孟广武.区间值模糊综合评判及其应用[J].系统工程理论与实践，2001，21（12）:81-84.ZHANG Xing-fang，GUAN En-rui，MENG Guang-wu.Intervalvalued fuzzy comprehensive evaluation and its application[J].Systems Engineering Theory Practice，2001， 21（21）:81-84.

[6]杨伟杰，裴玉龙，徐秋实.模糊数学在城市交通政策评价中的应用[J].公路，2003（4）:103-105.YANG Wei-jie，PEI Yu-long，XU Qiu-shi.Interval-valued fuzzy comprehensive evaluation and its application[J].Highway，2003（4）:103-105.

[7]卫小伟.城市智能交通控制系统研究与设计[J].现代电子技术，2010（17）：189-192.WEI Xiao-wei.Design and application of urban intelligent traffic control system[J].Modern Electronics Technique，2010（17）：189-192.