盲分离与时频分析融合的多源信道均衡

李 军 ，王 凯 ，康春玉

（1.海军大连舰艇学院 信息与通信工程系，辽宁 大连 116018；2.大连东软信息学院 计算机科学与技术系，辽宁 大连 116023）

线性调频（LFM）信号是非平稳信号的典型代表，广泛应用于主动声纳、水声通信等领域，LFM信号的参数估计可以采用解线调、Radon-Wigner变换[1]和最大似然估计[2]等方法。由于水声信道是一个非常复杂的时变、空变、频变信道，具有传播损失大、多途效应、频散效应严重等特点，这些都将使水声信号产生畸变。以往的LFM信号参数估计多是在单源且只含噪声的条件下进行的，很少考虑多信源条件下，强多途信道的影响，因此不适合处理复杂的多源水声信号。

目前的多源信道均衡技术有基于二阶统计的子空间方法[3]、QR分解方法[4]以及基于自适应滤波的 LMS、RLS方法等，这些方法主要针对通信信号，要求信号独立同分布，不适合线性调频（LFM）信号、单频脉冲信号的处理。针对多信源条件下强多途干扰严重的水声信道，采用一种盲分离与时频分析融合的多源信道均衡技术，实现了对CW和LFM信号的复原。

1 基本理论

假设声场环境中有N个相互独立的源信号si(i=1,2,…,N)经过多源水声信道响应矩阵 A(A=[aij]M×N，aij是第 j个源到第i个传感器的信道冲激响应）传输到M个传感器，所得观测信号为 xi(i=1,2,…M)，写成矩阵形式有：X=A⊗S+N，式中 N∈RM×l代表每个传感器上的加性噪声。

基于盲分离与时频分析融合的多源信道均衡技术的基本思想为：首先应用盲分离技术中的时延去相关算法(TDSEP)从接收数据中区分出每个源信号；然后对受多途干扰严重已经畸变的声源信号进行径向高斯核(RGK)时频分析，获得信号的时频分布图；最后应用Radon变换估计出声源信号瞬时频率和调频斜率进行解卷和信号重构。

1.1 基于时延去相关的盲分离算法

论文选取在水声领域中效果较好、性能稳定的时延去相关算法[5]TDSEP(Temporal Decorrelation source SEParation)进行研究，该方法是基于一组时延相关矩阵（二阶累积量）的盲源分离算法。它首先对阵元域输出进行预白化处理，定义一组时延相关矩阵，通过一个旋转矩阵对这组相关矩阵进行雅克比旋转得到它们的联合对角化矩阵，最后对混合矩阵的估计值进行求解得到其估计值=W-1Q。此时，源信号的估计值为 S=Hx，其中 H 是的逆矩阵。

1.2 基于径向高斯核的时频分析算法

时频分析的任务是描述信号的频谱含量怎样随时间变化，完成信号从时域到时频域的转换，以便能够在时间和频率上同时表示信号的能量和强度。本文采用一种可有效抑制交叉项干扰的径向高斯核[6]RGK(Radially Gaussian Kernels)时频分析方法。

对于信号s(t)，其 Cohen类时频分布TFR(t,f)可以由该信号的加权模糊函数的二维傅里叶变换得到：

ψ(τ,ν)是核函数，As(τ,ν)是 信 号的模糊函数AF(Ambiguity Fuction)

式中：*表示复数共轭；τ、ν分别代表时移和频偏。根据核函数的不同，会产生各种不同类型的时频分布。RGK算法在给定信号情况下依据一定的规则自适应地确定一个最优的径向高斯型低通核函数，从而可以得到所需的信号项区域，不但能够满足重要的时频分布性质，具有较强的噪声抑制能力，而且对信号的种类没有限制，特别适合于有限长度时间信号的分析。

1.3 基于Radon变换的声源信号参数估计

Radon变换是一种直线积分的投影变换，将原直角坐标旋转α角得到新的直角坐标 (u,v),这时以不同的u值平行于v轴积分，所得结果即为Radon变换。利用它能够估计出二维平面(可以是时频面)中指定直线的斜率（估计LFM信号的调频斜率）。对接收信号进行RGK时频分析运算后，对其时频分布数据进行Radon变换，然后搜索最大谱峰对应的角度αe,则LFM信号调频斜率的估计值为当估计出LFM信号的调频斜率后，构造解线调参考信号：

将之与接收信号sr(t)相乘有：

由于 ke≈k，于是信号 f(t)近似变成了单频信号，频率f0可作为LFM信号的初始频率估计。

2 实验数据验证

2.1 仿真数据验证

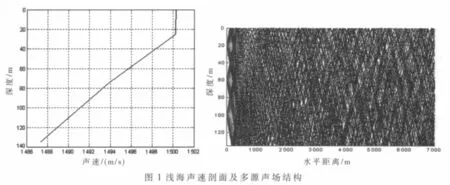
设同时发射3个声源信号，声源 1(LFM信号)：深度20 m，调频范围 1～5 kHz；声源 2(CW 信号)：深度 60 m，频率 2 kHz；声源 3(CW 信号)：深度 100 m，频率 4 kHz。用BELLHOP射线理论计算声场并构建浅海信道模型，信道冲激响应根据声场数据得到。浅海声速剖面及多源声场结构如图1所示，垂直接收阵深度27～30 m，阵元间距1 m，接收距离 5.6 km。 若声线数 80，声源发射角±11°，系统采样频率20 kHz，通过计算，声源1对应的信道响应如图2所示。设接收信噪比为0 dB，4个阵元的接收信号及使用TDSEP算法进行盲分离后信号对应的RGK时频分布如图3和图4所示。

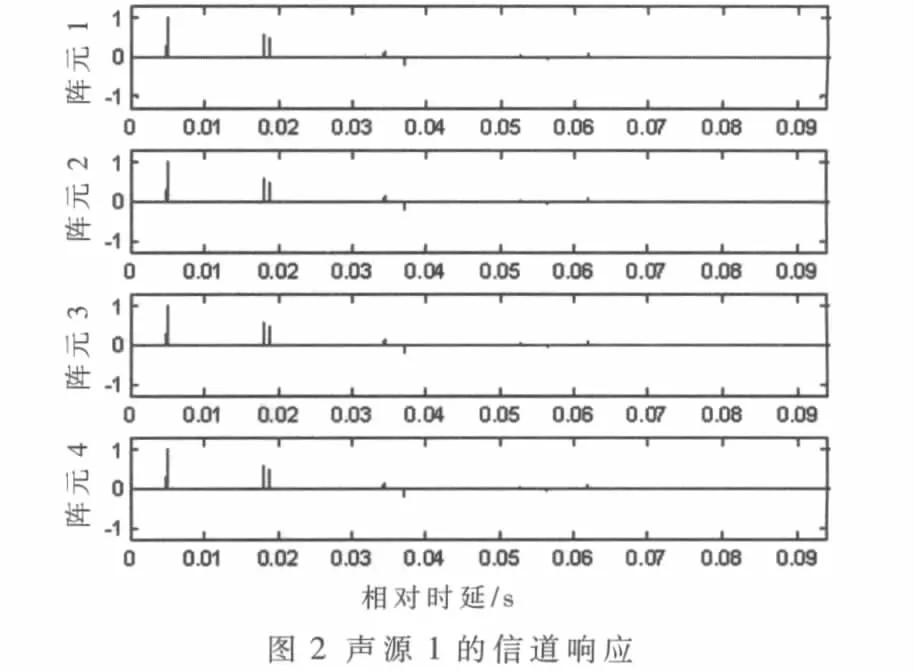
仿真结果表明，单阵元采集的接收数据难以将多声源信号区分开 （从图3可以看到，3个信号混在一起），更无法直接进行信号恢复。通过阵列接收和盲分离处理可以将 3个声源信号完全区分开，如图4(a)、(b)、(d)所示，这时分离出的信号可以看成是远端同时发射的多声源信号经过信道传输后分别在接收阵前产生的畸变信号，从 图4(b)也可以清晰看到，多途信道对线性调频信号的影响非常明显。

表1 3个声源信号参数估计结果

分别利用图4(b)、(d)、(a)的时频域数据恢复声源 1、2、3，所对应信号的参数估计结果如表1所示，各声源信号与重构信号时域波形的时域相关系数如图5所示，该图的横坐标与信号的时间坐标相对应，纵坐标是对声源信号和重构信号取相同长度（采样点数）所求出的相关系数值，可以看出各组信号的相关系数均达到0.81以上。

仿真结果表明，声源信号波形恢复效果较好，利用4个接收阵元可以成功完成3个声源信号在典型浅海信道条件下的盲解卷。

2.2 实测海试数据验证

为了进一步验证算法的有效性，在大连老虎滩以南海域进行了海试实验，一条船为接收船，两条船为发射船。发射船在接收船正横方向距离4 km、以大约2°夹角静止不动（两发射船间距约为140 m），辅机供电。两条船同时发射信号,发射船1发射信号1为3.2 kHz～5.2 kHz的线性调频脉冲信号，脉宽为20 ms，发射船2发射信号2为4.2 kHz的连续单频信号，系统采样频率为48 kHz，发射声源级约为170 dB。

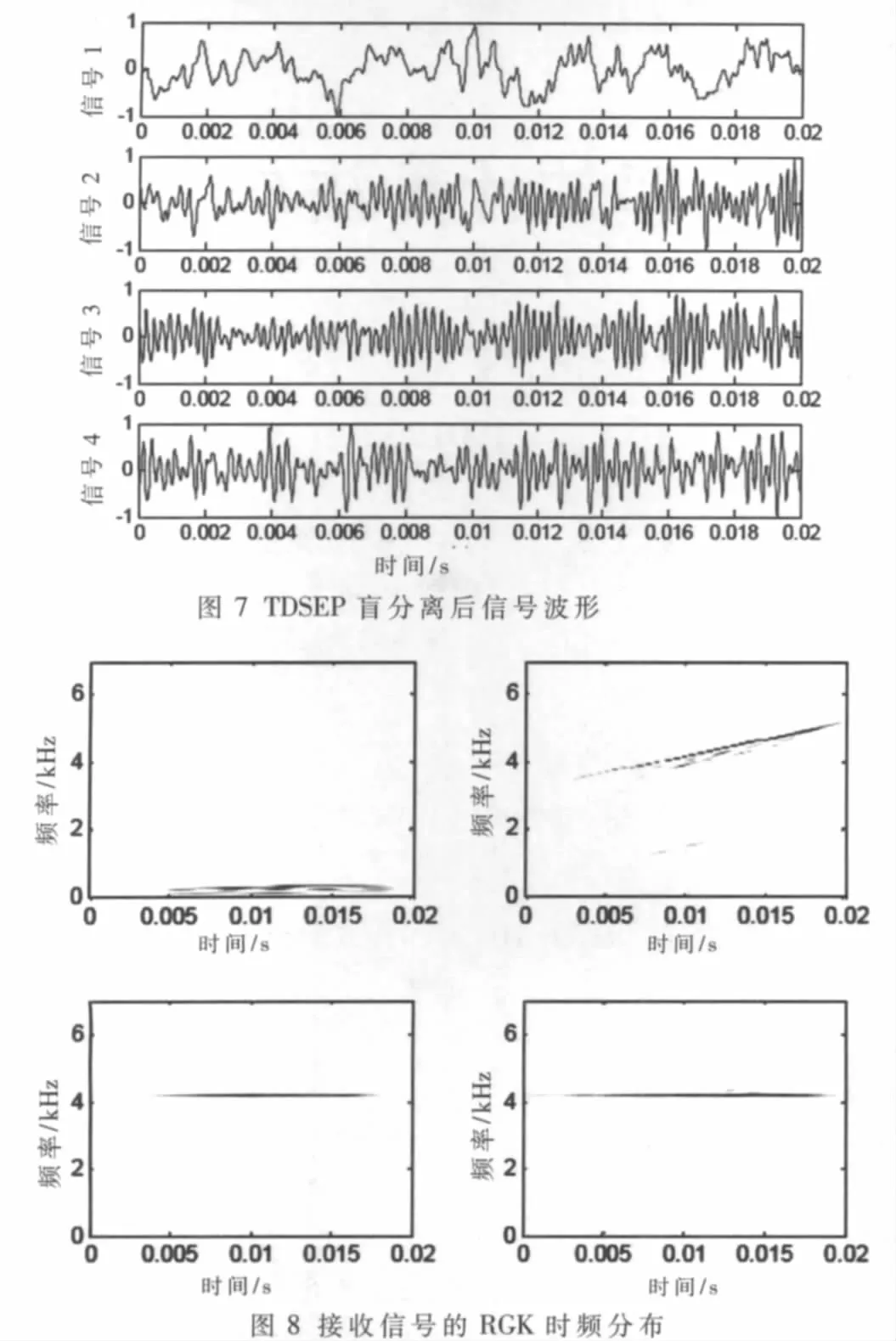
选取4路阵列接收数据进行分析。图6和图7给出了所截取信号及其盲分离后信号的波形。图8和图9为对所截取信号及其盲分离后信号进行RGK时频分析的结果。观察图8可以看出，接收信号是由两个声纳信号(3.2 kHz～5.2 kHz调频、4.2 kHz 单频)和各 种噪 声(舰 船辐射噪声、海洋环境噪声)构成，通过盲分离后各种信号基本分离开。分别利用图9(b)、(c)的时频域数据恢复声源1、声源2，所对应信号的参数估计结果如表2所示，利用该表中数据对原信号进行重构，进而完成信号的复原。通过计算相关系数来测试算法的有效性，信号1与图6中截取信号2的相关系数为0.276 7，与图7中盲分离后信号2的相关系数为0.404 3；信号2与图6中截取信号3的相关系数为0.321 6，与图7中盲分离后信号3的相关系数为0.475 5，而信号1和信号2与重构信号的相关系数均达到0.83以上。可以看出，接收信号与原信号的相关系数较低，经过盲分离后相关系数有所提高，通过时频分析重构运算后信号波形基本恢复。

本文将一种盲分离与时频分析融合的多源信道均衡技术应用在强多途干扰严重的水声信道，实现了在多个发射信源条件下对CW和LFM等典型声纳信号的估计。通过对仿真和海试数据的处理，验证了该方法具有较高的估计精度，对提高主动声纳探测效果具有很强的实用价值。

表2 两个声源信号参数估计结果

[1]WOOD J C,BARRY D T.Linear signal synthesis using the Radon Wigner transform[J].IEEE Trans on SP,1994,42(8)：2105-2111.

[2]冯晓平,李晨阳.线性调频信号参数快速估计[J].系统工程与电子技术,2005,27(2)：237-239.

[3]郑勇,冯大政.基于子空间的多输入多输出信道盲辨识与均衡[J].自然科学进展,2006,4(16)：463-468.

[4]丛进,杨绿溪.基于QR分解的MIMO信道盲辨识和盲均衡方法[J].电子学报,2004,32(10)：1589-1593.

[5]ZIEHE A,MULLER K R.TDSEP—an efficient algorithm for blind separation using time structrure inproceedings[C].ICANN98,2th September,1998：675-680.

[6]李蓉艳,马远良,杨坤德.浅海水声信道响应的盲估计[J]. 声学学报,2007,32(1)：10-18.