小波包变换用于双模噪声的信号检测

吴雪莲， 山拜·达拉拜

（新疆大学 信息科学与工程学院，新疆 乌鲁木齐 830046）

0 引言

非高斯噪声在信号分析和处理中具有重要的应用和研究价值。在通信和控制系统中，非高斯是比较常见的噪声信号，传统的信号检测办法是将其看为高斯噪声来处理，这在部分情况下是准确的，但是由于现代通讯科学的发展，无线电发射和接受设备的增加，功率源的增加，若是将干扰的噪声视为高斯噪声来处理，就会是检测结果不准确，很可能会破坏接收机的性能。研究一类非高斯噪声——双模噪声中的信号的检测与识别问题，将小波包良好的时频分析性能用于双模噪声背景下信号的识别和检测，并将此方法与经典检测系统的性能做了比较，实仿真结果表明，小波包方法优于经典检测系统方法。

1 双模噪声的模型分析

实际中，噪声通常是混合噪声，它们或许是双模的或许是多模的。双模噪声它是一种简单混合噪声，其研究方法要比高斯噪声复杂一些，但是可以代表混合噪声的一些特性。下面要研究高斯过程叠加均匀相位振荡过程以及高斯过程叠加码间干扰过程。首先看一下双模过程主要有3种简化模型[1-2]。

1)高斯过程G加均匀相位振荡过程Acosφ，概率密度为：

式中，σ是高斯分量的方差，莱斯衰落信道中的总噪声可看成双模噪声。当然，莱斯衰落信道中的噪声可以分为两种情况：①均值不为零的高斯噪声，即高斯噪声迭加固定相位振荡波；②双模噪声。

2)高斯过程G加码间干扰过程a(t)=±a，其概率密度函数为：

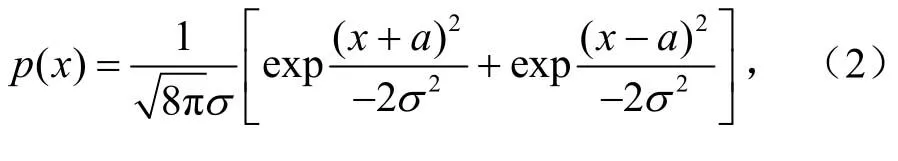
当a＜σ/3时，可以把它等效为高斯过程。3)当a＞2σ时，概率密度可以写成：

式中，Φ(x)为标准正态分布，sign(x)为符号函数。当然，如果模型1中时，模型2中a＜σ时，概率密度函数只有一个峰值，此时可按功率相等把双模噪声等效为高斯噪声。

2 小波基本原理

小波分析是20世纪80年代后期形成的一个新兴的数学分支，它是建立在泛函分析、调和分析、傅里叶分析基础上的时频原子。其在时域和频域同时具有良好的局部化特性和多分辨率特性，常被誉为“数学显微镜”[3]。小波包是由 Coifan、Meyer及Wickhauser引入的。他们在研究正交小波基的基础上创立了正交小波包的概念，后来又发展到半正交小波包和广义小波包[4]。将小波变换用于双模噪声背景下的信号检测，得到一个小波包信号检测系统并将其与经典检测系统进行比较，检测结果有一定的提高。

2.1 小波变换基本概念

对于任意函数f(x)∈L2(R)的连续小波变换[5]：

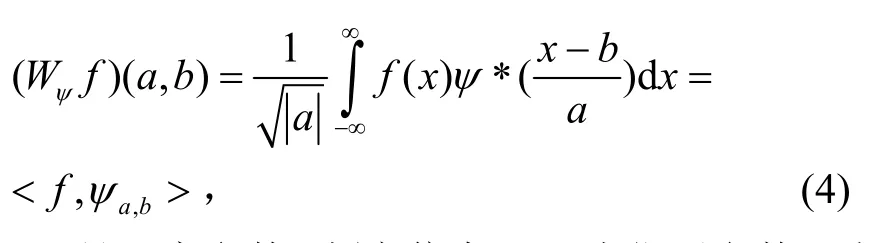
式中，a是尺度参数（频率信息），b为位置参数（时空信息），ψ(x)为小波母函数，且

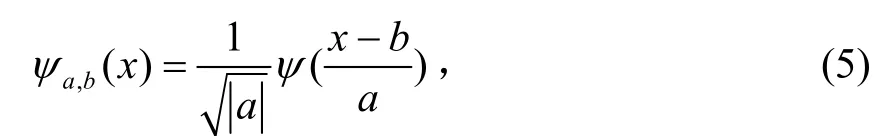
频域上则有：

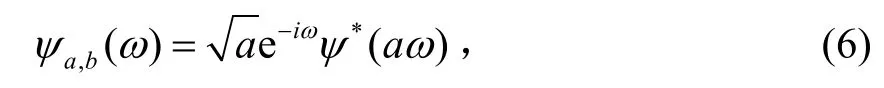
2.1.2 小波包变换

正交小波包，粗略的可以理解为是一函数族，由它们可构造L2(R)的标准正交基库，从此库中可以选出L2(R)的许多组标准正交基库，通常正交小波基使其中的一组。小波函数是小波包函数组中的一个。所以小波包是小波函数的推广[5]。

设{hn}n∈Z是正交尺度函数φ(t)对应的正交低通实系数滤波器，{gn}n∈Z是正交小波函数ψ(x)对应的高通滤波器，其中gn=(-1)nh1-n，则它们满足以下两尺度方程和小波方程：

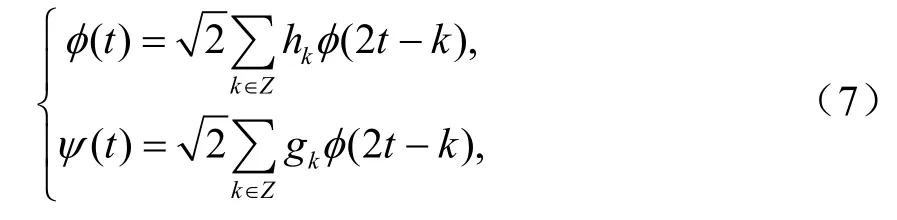
通过φ(t)、ψ(t)、g、h在固定尺度下可定义一组称为小波包的函数[6-7]。

小波包可以用一个完全的二叉树来表示：其中二叉树左，右子树上的系数分别是g和h。

从多分辨分析的角度来看，小包分析就是对L2(R)进行正交和分解，即：

而小波包是对小波空间Wj进行更精细的分解，使得在新的标准正交基下，能够对包含大量细节的信号进行更好的时频局部化分析[8-9]。

2.2 模型1,2,3的高斯化分析

对上文提到的双模噪声进行小波包变换，来观察一下这种方法的高斯化效果。

2.2.1 模型1的高斯化效果

高斯噪声加均匀相位振荡过程，其中，高斯噪声均值为 0，方差为 1，均匀相位振荡过程为2.5cosθ(t)，概率密度为式（1）。

这里选用sym15小波波函数和log energy熵，分解尺度为5，选用100 000个采样点，图1列出了模型 1的小波包变换系数在子空间[2,1]的概率分布的直方图。由图1可以看出很接近高斯分布。

图1 模型1的小波包变换系数在子空间[2,1]的概率分布的直方

2.2.2 模型2的高斯化效果

高斯噪声叫码间干扰过程，b(t)=±b,b=1.5，±b的概率均为0.5，高斯噪声均值为0，方差为1。概率密度函数为式（2），选用db20小波波函数和log energy熵，分解尺度为5，选用100 000个采样点，图2列出了模型2的小波包变换系数在子空间[2,2]的概率分布的直方图。图 2反映出在[2,2]子空间上的高斯化效果比较好。

2.2.3 模型3的高斯化效果

在模型 2中当a＞2σ时，模型 2就为模型 3即，b(t)=±b,b=2.5，±b的概率均为0.5，高斯噪声均值为0，方差为1，概率密度函数为式（3），选用sym15小波波函数和log energy熵，分解尺度为5，选用100 000个采样点，模型3的小波包变换系数在子空间[2,2]的概率分布的直方图。同样，在此空间上高斯化效果很好，如图3所示。

图2 模型2的小波包变换系数在子空间[2,2]的概率分布的直方

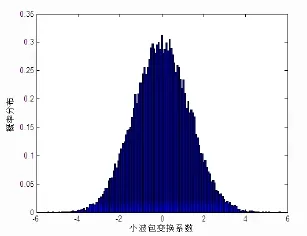
图3 模型3的小波包变换系数在子空间[2,2]的概率分布的直方

3 小波包检测系统的系统模型

考虑二元检测假设检验问题：

式中，x(t)是已知的确知信号，s(t)是以上提到的非高斯噪声。

假设i尺度上某一子空间的信号的小波包变换是：是根据有用信号的大致的频率分布来决定需要分析输出的子空间的编号，Wx是信号的小波包变换。对应的在相应子空间上噪声的小波包变换为Wsj(k)，j=1,2,…,N＜2i。信号检测过程如图4所示。

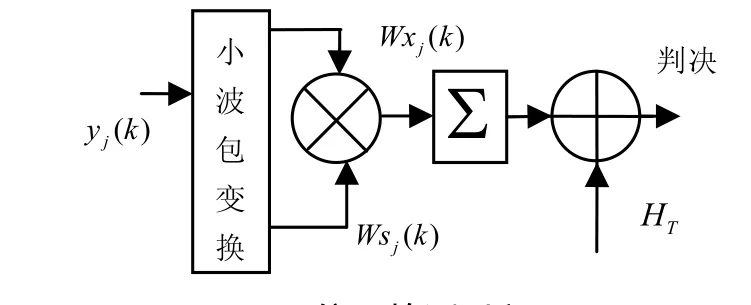
图4 信号检测过程

有前面的分析，设

那么，判决准则为：

4 数据仿真及结果分析

根据图4，分析在虚警概率为0.01时模型1的小波包变换检测系统和经典检测系统的检测概率。

信号的占空比为0.5，长度N=172-2，噪声s(t)是双模过程（模型1）。图5是信噪比和检查概率曲线，小波包变换的检测效果要优于经典检测系统的检测结果，当信噪比是10 dB的时候，小波包检测系统的检测概率几乎达到了 1，而经典检测系统的检测概率不到0.85。

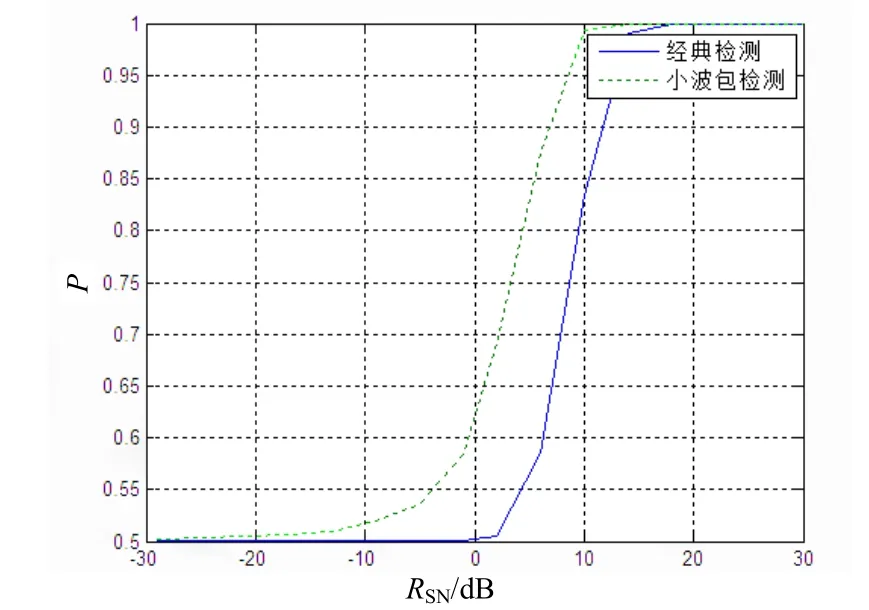
图5 检测概率

5 结语

传统的信号处理理论一般是建立在高斯噪声基础上的。但是在实际问题中这种假设往往难以满足要求。利用小波包的良好的时频分析能力，将小波包变换应用于双模噪声背景下的信号检测与识别的问题，将3种双模噪声在一定的尺度下进行小波包变换，将其在该尺度上等效为高斯噪声，此时就可以用经典的信号检测于识别的方法进行信号的检测与识别。实验的仿真结果图5证明该方法优于经典的信号检测方法，此方法有一定的使用价值。

[1] 黄玉划，山拜·达拉拜.双模噪声中号的检测[J]. 电路与系统学报，2002,7（01):37-40.

[2] 山拜·达拉拜，黄玉划. 几类非高斯噪声模型转换的研究[J]. 电子学报，2004,32(07)：1 090-1093.

[3] 葛哲学，沙威.小波分析理论与MATLAB R2007[M].北京：电子工业出版社，2007:240-245.

[4] 孙延奎.小波分析及其应用[M].北京：机械工业出版社，2005:78-83.

[5] 段凤增.信号检测理论[M].哈尔滨：哈尔滨工业大学出版社，1988:102-103.

[6] 薛年喜.MATLAB在数字信号处理中的应用[M] .北京：清华大学出版社，2003:146-148.

[7] 樊昌信. 通信原理 [M].北京：国防工业出版社，1995：58-61.

[8] 程正兴.小波分析算法与应用[M].西安：西安交通大学出版社，1998:64-70.

[9] 李冠，吴尽昭，范明钰.基于小波的信号去噪分析[J].通信技术，2010,43（09）：79-84.