Optimization and coordination of South-to-North Water Diversion supply chain with strategic customer behavior

Zhi-song CHEN, Hui-min WANG*

1. Business School, Nanjing Normal University, Nanjing 210023, P. R. China

2. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098, P. R. China

Optimization and coordination of South-to-North Water Diversion supply chain with strategic customer behavior

Zhi-song CHEN1,2, Hui-min WANG*2

1. Business School, Nanjing Normal University, Nanjing 210023, P. R. China

2. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098, P. R. China

The South-to-North Water Diversion (SNWD) Project is a significant engineering project meant to solve water shortage problems in North China. Faced with market operations management of the water diversion system, this study defined the supply chain system for the SNWD Project, considering the actual project conditions, built a decentralized decision model and a centralized decision model with strategic customer behavior (SCB) using a floating pricing mechanism (FPM), and constructed a coordination mechanism via a revenue-sharing contract. The results suggest the following: (1) owing to water shortage supplements and the excess water sale policy provided by the FPM, the optimal ordering quantity of water resources is less than that without the FPM, and the optimal profits of the whole supply chain, supplier, and external distributor are higher than they would be without the FPM; (2) wholesale pricing and supplementary wholesale pricing with SCB are higher than those without SCB, and the optimal profits of the whole supply chain, supplier, and external distributor are higher than they would be without SCB; and (3) considering SCB and introducing the FPM help increase the optimal profits of the whole supply chain, supplier, and external distributor, and improve the efficiency of water resources usage.

South-to-North Water Diversion; supply chain; strategic customer behavior; floating pricing mechanism

1 Introduction

The South-to-North Water Diversion (SNWD) Project is a significant initiative meant to help solve the water shortage problems in North China, and a global-scale strategic water resources engineering project related to the sustainable development of China’s economy. The project is divided into the Eastern Route Project, Western Route Project, and Middle Route Project, transferring water resources from the Yangtze River, and linking the Yangtze River, Huaihe River, Yellow River, and Haihe River to form huge water systems.

Currently, the Eastern Route Project is due for completion and is going to be put into operation. However, the optimal operation theory and relevant practice of water diversion projects are still not sufficient. Many scholars have tried to apply the supply chain idea to optimal allocation and scheduling of inter-basin or transboundary water resources, have developed the concept and models of the water resources supply chain, and have also done some initial research on corresponding issues. Since water resources allocation and scheduling is characterized by planning and collaboration, and supply chain management is characterized by overall coordination and maximized benefits, Wang et al. (2004) and Wang and Hu (2005) thought that it was feasible and suitable to apply supply chain management to operations of the SNWD Project. A lot of research on supply chain management applied to optimal allocation and scheduling of inter-basin water resources in the SNWD Project has been done; concepts and basic models of the water resources supply chain have been developed; logistics flow, information flow, and cash flow in the water resources supply chain have been defined; and inventory management, logistics management, the bullwhip effect and risk management, and coordination of the water resources supply chain have been studied. Wang et al. (2008) built a principal-agent contract model and pricing model for the SNWD supply chain; Zhu et al. (2005, 2006), Zhu and Wang (2005), and Zhu (2007, 2008a, 2008b) designed the water resources supply chain structure for the Eastern Route of the SNWD Project, analyzed the bullwhip effect, and built a water resources allocation model and inventory management model; Zhang et al. (2004, 2005) built a multi-stage coordination model for the SNWD supply chain; Hou et al. (2008a, 2008b, 2009) built minimum commitment and flexibility contracts, a vendor-managed inventory (VMI) coordination model, and a stock replenishment and shipment scheduling (SRSS) model for the SNWD supply chain; Zhang et al. (2008) built a pricing model for the SNWD supply chain; and Chen et al. (2010) and Chen and Wang (2010) studied the relationship between social responsibility and economic benefit in SNWD Project operations management, researched the optimal problem of the SNWD supply chain under quasi-market conditions, and built the newsvendor optimization model of the SNWD supply chain with random rainfall under unrelated demand-rainfall conditions and related demand-rainfall conditions.

In operations management of the SNWD supply chain, end-customers may choose to order water resources immediately or delay ordering water resources when the sale season is coming. This decision depends on the customers’ expectation of the future price and utility and the profit maximization. These kinds of customers are usually called strategic customers or forward-looking consumers. In the past, there has been some research on the forward-looking behavior of consumers. Jacobson and Obermiller (1990), Krishna et al. (1991), Krishna (1994), and Ho et al. (1998) studied the formation of expected future prices, the impact of dealing patterns on purchase behavior, and consumer perceptions of promotion activity. Recently, a lot of studies have combined strategic consumers with supply chain pricing and inventorymanagement to consider their mutual impact on optimal pricing, ordering, and performance. Aviv and Pazgal (2008) studied the optimal pricing of seasonal products in the presence of forward-looking consumers; Elmaghraby et al. (2008) designed optimal pre-announced markdowns in the presence of rational customers; Yin et al. (2009) studied inventory management and optimal markdown pricing policy in the presence of strategic customers; Liu and van Ryzin (2008) studied the impact of strategic capacity rationing on early purchases; Su (2007, 2010a, 2010b) and Su and Zhang (2008, 2009) researched inter-temporal pricing with strategic consumer behavior, the consumer stockpiling, the impact of commitment on supply chain performance with strategic consumer behavior, and the optimal pricing in the presence of speculators and strategic consumers; and Cachon and Swinney (2009, 2011) researched the relationship between rapid production, enhanced design, and strategic consumer behavior. Most of the available research focused on the impact of strategic customer behavior (SCB) on pricing and inventory management of industrial product supply chains. However, the impact of SCB on pricing and inventory management of water resources product supply chains is still insufficient.

Traditional water resources allocation put one-sided emphasis on collective rationality and social benefit maximization from the perspectives of technique optimization, ignoring the impacts of individual rationality and customer behavior. The water resources management in the new period is characterized by communication and coordination, emphasizes the coordinated optimization between individual rationality and collective rationality, and takes the customer behavior into account, which is worth studying and practicing.

Usually, demand is random and supply is certain in common product supply chains. In contrast, water supply is random and water demand is relatively certain in the Eastern Route of the South-North Water Diversion (ERSNWD) Project supply chains. Due to the stochastic characteristic of precipitation, there is some uncertainty of the water storage and inflow; this kind of uncertainty causes the randomness of the water supply, which is different from that of common product supply chains. Sometimes, precipitation which is much more than that in a normal year makes the water supply larger than the end-user’s demand. In this situation, to sell the excess water at a salvage price benefits the distributor and the whole supply chain. In contrast, when precipitation is much less than that in a normal year, water supply is less than demand. In this situation, to delay ordering with a punishment fee and to sell the water later at a higher price with a second ordering opportunity also benefits the distributor and the whole supply chain. This kind of pricing mechanism is called a floating pricing mechanism (FPM). It helps in the implementation of water resources savings and the improvement of water resources efficiency. Under the FPM, the impact of customer behavior becomes more important. In the SNWD water resources supply-demand system, there are four kinds of customers: industrial customers, residential customers, agricultural customers, and ecological customers, and the main customers are the industrial customers and residential customers.

Owing to the existence of some water storage for these customers, they are able to order water resources immediately at full price or wait to order water resources at a discount price to maximize expected utilization, according to their beliefs about their opportunity to obtain water resources at a salvage price and the corresponding rational expectations equilibrium. Hence, this kind of customer is a strategic customer. Therefore, it is necessary to study optimal operations of this special kind of supply-demand system with the FPM and SCB. This paper introduces the FPM and SCB into the SNWD supply chain decision, builds a centralized optimization model and a decentralized optimization model respectively for three cases, and constructs corresponding coordination mechanisms. Finally, this paper presents some numerical analysis.

2 Definition and assumptions of SNWD supply chain

The ERSNWD Project is a large complex inter-basin system with multiple sources, multiple objectives, and multiple projects for pumping, storage and water supply to achieve rational water distribution in North China. It is being constructed and extended with a total investment of 6.5×1010yuan based on the project of water transfer from the Yangtze River to the North Plain of Jiangsu Province. The ERSNWD Project transfers water from the Yangtze River to supplement water resources for Tianjin, in the eastern part of the North China Plain, and the Shandong Peninsula, where it is combined with the Yellow River Diversion Project and the Middle Route of the SNWD Project to solve the water shortage problems in more than 25 cities. Through structural analysis of the ERSNWD system, we can generalize the ERSNWD as a water resources supply chain system composed of the local sub-system and the external sub-system. The local sub-system mainly includes Hongzehu Lake, Luomahu Lake, Nansihu Lake, pumping stations, sluice gate stations, and regulation-storage reservoirs, and the main operations agent is the Jiangsu Shuiyuan Corporation. The external sub-system mainly includes Dongpinghu Lake, Qianqinwa Lake, Dalangdian Lake, Beidagang Lake, pumping stations, sluice gate stations, and regulation-storage reservoirs, and the main operations agent is the Shandong Ganxian Corporation. In our research, we considered the Jiangsu Shuiyuan Corporation as the local supplier (S), and the Shandong Ganxian Corporation as an external distributor (ED). The lead time of water diversions and extreme flood or drought disasters are not considered in this paper. We combine the water conveyance loss, evaporation, and runoff with the initial water storage as the original water resources supply sources, and the rainfall in the external sub-system is a free external water resources supply source while the water diversion from the Yangtze River is an expensive water resources supply source. We assume that the total supply of water resources is capable of satisfying local demand, and there is a certain quantity of water resources satisfying the external distributor.

In order to model the optimal operation problem of the SNWD Project, we set variablesand parameters as follows: Q is the water resources ordering quantity of the external distributor; p is the retail price of unit water resources for the external distributor; w is the wholesale price of unit water resources for the local supplier; c is the average unit cost of water transfer for the local supplier; csis the average unit cost of second water transfer for the local supplier, satisfying the condition cs＞ c; h is the unit water resources holding cost for the external distributor; b is the unit water resources shortage cost for the external distributor; ϕ is the usage rate of precipitation for the external distributor, satisfying the condition 0 ≤ ϕ＜ 1; uHis the unit utility of strategic customers if they choose to order water resources immediately; uLis the unit utility of strategic customers if they choose to delay ordering water resources, satisfying the condition uH＞ uL; r is the reservation price of unit water resources for strategic customers; α is the rate of increase of the unit water resources retail price if the external distributor orders water resources for a second time; β is the rate of decrease of the unit water resources retail price if the external distributor sells excess water resources, satisfying the condition 0 ≤ α＜ 0.5 ＜ β＜ 1; S is the original quantity of water resources storage for the external distributor; D is the demand quantity of water resources for the external distributor; and R is the precipitation in an external market. R is a random variable, satisfying the conditionR ≤ R ≤ R, withR andR being the minimum and maximum precipitation in the external market over N years, respectively; the cumulative density function and probability density function of R are F (R ) and f(R ), respectively, satisfying the conditionsF (R )≈ 0 and F(R )≈ 1, and we defineF(R ) = 1− F(R).

The following conditions were applied in this study: (1) h + c ＞ (1 − β)p; (2) cs− c ＞ αp; and (3) βp ＞ uH− uL.

3 Optimization and coordination model with strategic customer behavior

As shown in the discussion mentioned above, due to the uncertainty of precipitation, the water supply and demand do not match each other, and excess water supply or water shortage always exists. The newsvendor model is a kind of mathematical model used to determine optimal inventory levels or ordering quantity for optimal production and inventory problems with uncertain demand or supply. Obviously, the newsvendor model is suitable for optimal operations of the ERSNWD supply chain. Therefore, the basic optimization and coordination model with the newsvendor form was built first, and then, the optimization and coordination model with the FPM was built. Finally, the optimization and coordination model with the FPM and SCB was built.

3.1 Case without SCB and FPM

The centralized decision model of the SNWD supply chain based on collective rationality and the decentralized decision model of the SNWD supply chain based on individual rationality were built, and the coordination between collective rationality and individualrationality was studied.

3.1.1 Centralized decision model of SNWD supply chain

The optimal problem for the centralized decision of the SNWD supply chain is as follows:

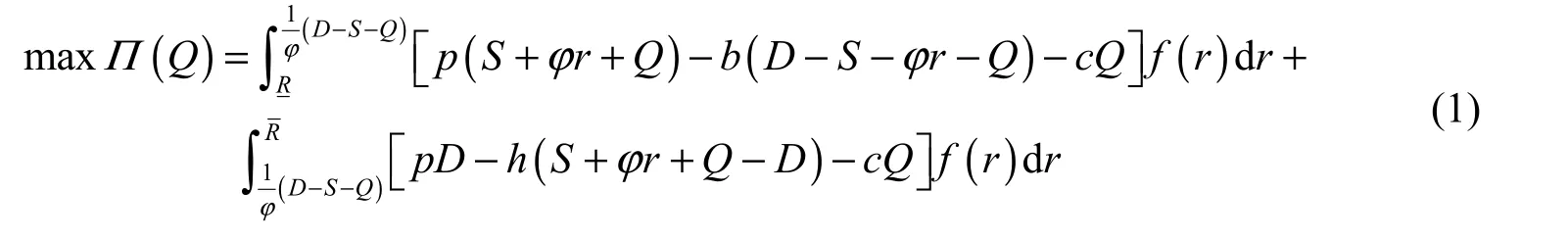
where Π (Q) is the expected profit function of the whole supply chain. Respectively solving the first-order condition and second-order derivative regarding Q of Π (Q), we found that the problem of Eq. (1) was a convex optimization problem, and we can obtain the optimal ordering quantity under the centralized decision satisfying the following condition:

whereCQ is the optimal ordering quantity under the centralized decision. Obviously, with the centralized decision, the optimal ordering quantity increases as the retail price p and shortage cost of unit water resources b increases, and decreases as the transfer cost c increases. As the optimal ordering quantity is obtained, the optimal profit of the supply chain under the centralized decision is easy to determine.

3.1.2 Coordination for decentralized decision model of SNWD supply chain

We assume that the external distributor shares 1 φ− of his revenue with the local supplier under a revenue-sharing contract, where φ is the proportion of retained revenue for the external distributor, and 0 1φ≤ ≤ . Therefore, the optimal problem for the external distributor under the decentralized decision is as follows:

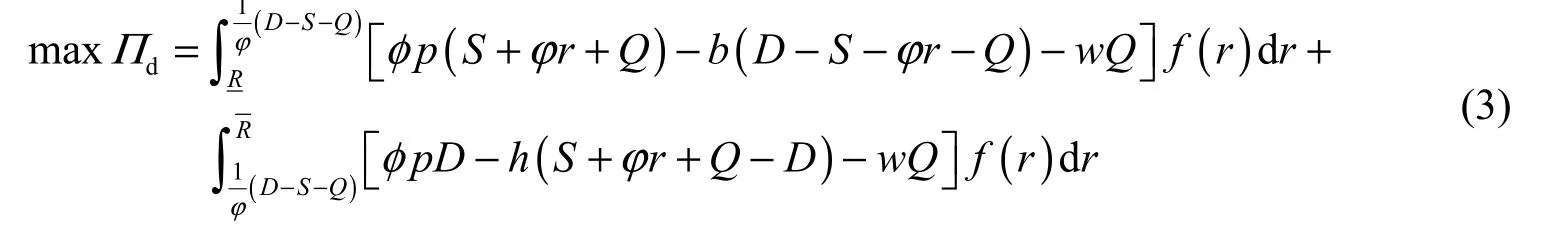
wheredΠ is the expected profit function of external distributor under the revenue-sharing contract. The structure of this problem is the same as the centralized decision condition. Respectively solving the first-order condition and second-order derivative regarding Q ofdΠ, we found that the problem of Eq. (3) was a convex optimization problem, and we can obtain the optimal ordering quantity under the decentralized decision satisfying the following condition:

whereDQ is the optimal ordering quantity under the decentralized decision. Apparently, the optimal ordering quantity for an external distributor increases as the retail price p and shortage cost of unit water resources b increases, and decreases as the wholesale price of unit water resources w increases.

To achieve the coordination under a revenue-sharing contract, the equation QC=QDneeds to be satisfied. Therefore, we have a coordination condition as follows:

whereCw is the coordinated wholesale price. Then, the corresponding optimal profit of the external distributor and local supplier under a revenue-sharing contract can be obtained.

3.2 Case without SCB and with FPM

As a result of random precipitation, there is always a water shortage or water oversupply in the water supply-demand process. Therefore, we introduce a kind of FPM. The mechanism is as follows: when a water shortage occurs, a local supplier provides second-ordering opportunity for an external distributor. The cost and price for the second ordering is higher than the usual ordering, and there is no shortage penalty; when a water oversupply occurs, the local supplier sells the excess water with a lower price than the usual price, achieving effective use of flood resources.

3.2.1 Centralized decision model of SNWD supply chain

The optimal problem for the centralized decision of the SNWD supply chain with the FPM is as follows:

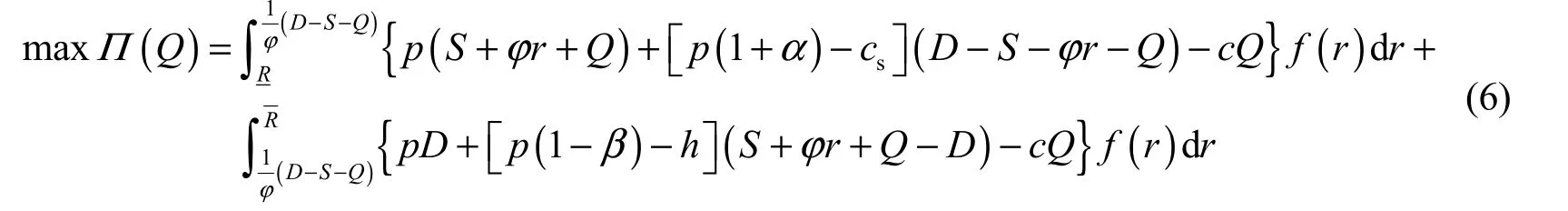
Respectively solving the first-order condition and second-order derivative regarding Q of Π (Q), we found that the problem of Eq. (6) was a convex optimization problem, and we can obtain the optimal ordering quantity under the centralized decision satisfying the following condition:

Clearly, under a centralized decision with the FPM, the optimal ordering quantity increases as the second transfer costsc increases, and decreases as the transfer cost c and rate of increase of the retail price of unit water resources α increases. As the optimal ordering quantity is obtained, the optimal profit of the supply chain under the centralized decision is easy to determine.

3.2.2 Coordination for decentralized decision model of SNWD supply chain

We assume that the external distributor shares 1 φ− of his revenue with the local supplier under a revenue-sharing contract, where 0 1φ≤ ≤ . Therefore, the optimal problem for the external distributor under the decentralized decision is as follows:

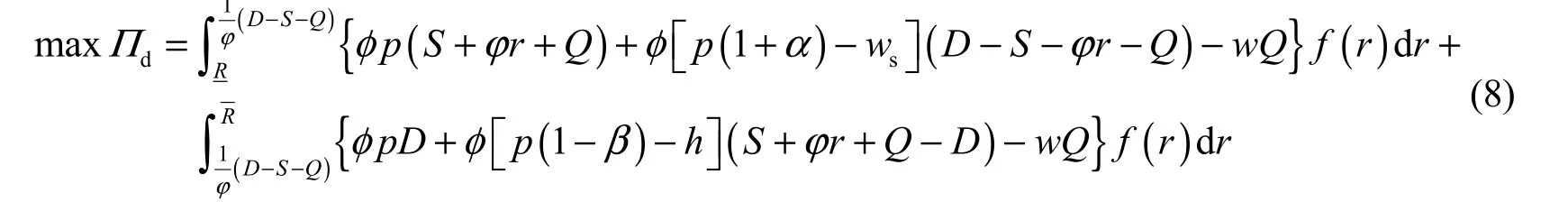
wheresw is the second-ordering wholesale price. Respectively solving the first-order condition and second-order derivative regarding Q ofdΠ, we found that the problem of Eq. (8) was a convex optimization problem, and we can obtain the optimal ordering quantity under the decentralized decision satisfying the following condition:

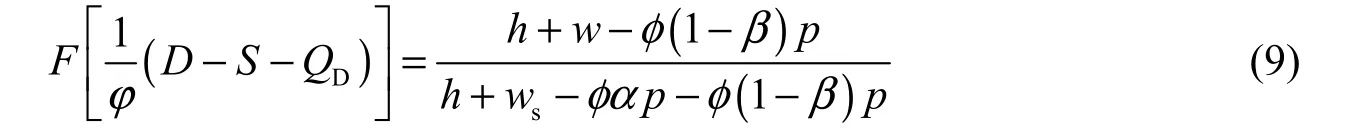
Evidently, with the FPM, the optimal ordering quantity for the external distributor increases as the second-ordering wholesale price wsincreases, and decreases as the wholesale price w and rate of increase of the retail price of unit water resources α increase.

To achieve coordination under a revenue-sharing contract, the equation QC= QDneeds to be satisfied. Therefore, the water diversion supply chain coordination can be achieved via the following linear combination:

wheresCw is the coordinated second-ordering wholesale price. As mentioned above, condition (2)sc c pα− ＞ was applied in this study, and then we havesΔ Δ＞ . Therefore, the corresponding optimal profit of the external distributor and local supplier under a revenue-sharing contract can be obtained under these coordinated conditions.

3.3 Case with SCB and FPM

Based on the model analysis mentioned above, we introduced strategic customers to our model, considering the impact of SCB on the supply chain decision and performance. Strategic customers are customers who order water resources immediately at the retail price p with water resources utility uH, or who delay ordering water resources at a higher price (1 +α)p (water shortage condition) or a lower price (1 − β)p (water oversupply condition) with utility uL. rPis the reservation price or willingness to pay in the regular selling season, and satisfies the condition (1 − β) p≤ c ＜ p＜ rP＜ uL＜ uH.

After introducing strategic customers, the external distributor needs to determine both the water resources ordering quantity Q and the water resources retail price p. Strategic customers are able to know the value of p, but are not able to know the value of Q. The expected probability of water oversupply for strategic customers isaξ. After finding the retail price p, strategic customers need to choose the reservation pricePr. The external distributor is not able to know the value ofPr, but is able to determine an expected evaluation valuerξ ofPr.

We adopted the following decision sequence: First, strategic customers have water resources demand D, and the external distributor is able to understand the demand. Then, the external distributor determines an expected evaluation value ξrof the reservation price, and chooses the optimal retail price p and ordering quantity Q. Then, strategic customers estimate the expected probability ξaof water resources oversupply, and determine their reservation price rP. Next, the random precipitation is considered the known precipitation. Then, the external distributor sells water resources at the retail price p. Finally, excess water resources are sold at the salvage price (1 − β)p, and shortage demand is satisfied by a second-ordering opportunity at a higher price (1 + α)p.

We first analyzed the strategic customers’ decision problem. Strategic customers’ expected surplus iswhere the first term is the surplus from ordering water resources immediately at the retail price p, and the second term is the expected surplus from delaying ordering water resources.

Obviously, the condition for strategic customers choosing to order water resources immediately at the retail price p is as follows:

Therefore, given an expected probabilityaξ, the reservation price of unit water resources for strategic customers is as follows:

We assume that information about expected probability ξaand reservation price rPis shared among homogeneous strategic customers, and also that strategic customers are risk-neutral. Obviously, given expected evaluation value ξr, the external distributor will choose p = ξrand Q(p ) =argmax Π(Q ,p)when he is making a pricing decision. According to the definition of rational expectations equilibrium (Su and Zhang 2008), we have a rational expectations equilibrium (p , Q, rP, ξa,ξr) satisfying the following conditions:

Obviously, rational expectations equilibrium conditions can be simplified as follows:

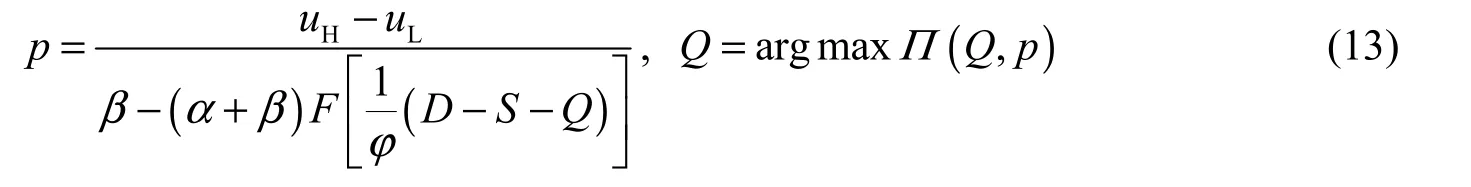
Then, we have

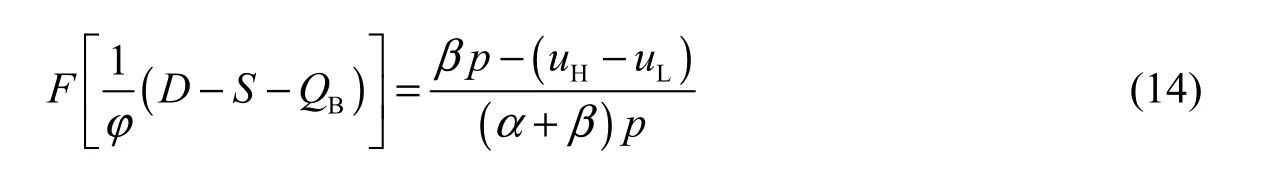
whereBQ is the optimal ordering quantity with SCB.

3.3.1 Centralized decision model of SNWD supply chain

Obviously, the optimal ordering quantity of the centralized supply chain under a rational expectations equilibrium satisfies the equation QB= QC. Then, we have an optimal price and ordering quantity for the centralized decision of the SNWD supply chain with SCB and the FPM as follows:

whereBCp is the rational expectations equilibrium retail price under the centralized decision, andBCQ is the rational expectations equilibrium ordering quantity under the centralized decision.

Explicitly, under a centralized decision with the FPM and SCB, the optimal ordering quantity increases as the second transfer costsc increases, and decreases as the transfer cost c and rate of increase of the retail price of unit water resources α increase. As the optimal retail price and ordering quantity are obtained, the optimal profit for the centralized supply chain is easily determined.

3.3.2 Coordination for decentralized decision model of SNWD supply chain

Obviously, the optimal ordering quantity of a decentralized supply chain under a rational expectations equilibrium satisfies the condition QB= QD. Then, we have an optimal pricing and ordering quantity for the decentralized decision of the SNWD supply chain with SCB and the FPM as follows:

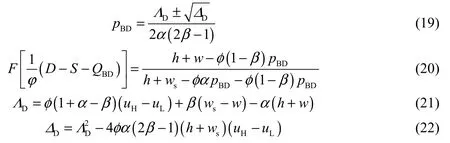
whereBDp is the rational expectations equilibrium retail price under the decentralized decision, andBDQ is the rational expectations equilibrium ordering quantity under the decentralized decision.

Clearly, with the FPM and SCB, the optimal ordering quantity for an external distributorincreases as the second-ordering wholesale price wsincreases, and decreases as the wholesale price w and rate of increase of the retail price of unit water resources α increase.

Under a revenue-sharing contract, to achieve coordination, it is necessary to make pBC= pBDand QBC= QBD. Then, we have a kind of coordinated condition ΛC= ΛDand ΔC= ΔD. Therefore, supply chain coordination can be achieved with the following conditions:

Under these coordinated conditions, the corresponding optimal profits of the external distributor and local supplier under a revenue-sharing contract can be obtained.

4 Numerical analysis

According to the SNWD overall plan and the corresponding reports, we set parameters as follows: The total water demand D is about 30 km3and the original storage S is about 10 km3. We assume that precipitation R obeys normal distribution, its mean is μ= 25km3, and its standard deviation is σ= 5km3; that is, R～ N (2 5,52).R= 0,R= 50km3, and the usage rate of precipitation for the external distributor is about 0.4. The dimensionless parameters are α= 0.15, β= 0.8, ϕ= 0.4, and φ= 0.75. According to some estimated data from the overall plan and corresponding reports, the average unit cost c of water transfer is about 0.25 to 0.35 yuan/m3. Therefore, we set c= 0.3 yuan/m3and cs= 0.7 yuan/m3. The retail price p is about 2 to 3 yuan/m3, thus we set p= 2 yuan/m3. Usually, the holding cost h is small and a shortage cost b is relatively large for water resources, thus we set h= 0.2 yuan/m3, and b= 0.4 yuan/m3. According to the corresponding economic data, a unit of water is able to produce a GDP of 3 to 5 yuan/m3. Therefore, we set μH= 5 yuan/m3, and μL= 4 yuan/m3. We carried out numerical analysis for three cases with Matlab R2010b. The numerical analysis results are shown in Table 1.

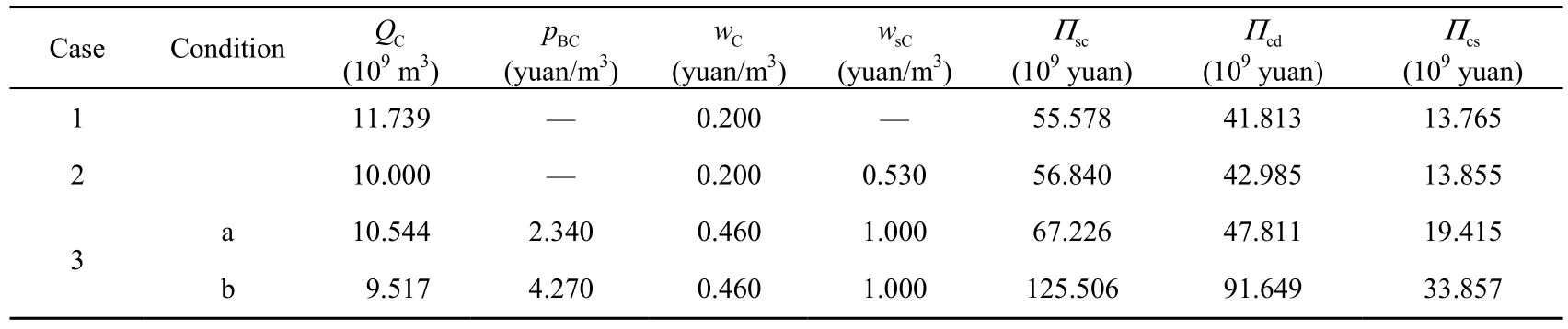
Table 1Numerical analysis results

Comparing all three cases, we can make the following conclusions:

(1) Comparing case 1 with case 2, when the supply chain achieves coordination, owing tothe water shortage supplements and excess water promotion policy provided by the FPM, the optimal water resources ordering quantity with the FPM is less than that without the FPM, the initial wholesale price with the FPM is almost the same as that without the FPM, and the second-ordering wholesale price is higher than the initial wholesale price. The optimal profits of the whole supply chain, local supplier, and external distributor with the FPM are higher than they would be without the FPM.

(2) Comparing case 2 with case 3, when the supply chain achieves coordination, the initial wholesale price and second-ordering wholesale price with SCB are higher than those without SCB. The optimal profits of the whole supply chain, local supplier, and external distributor with SCB are higher than they would be without SCB.

(3) For case 3, condition a means that strategic customers’ delaying ordering utility is higher than the retail price, i.e., strategic customers’ net profit is positive at the salvage sale phase; and condition b means that strategic customers’ delaying ordering utility is lower than the retail price, i.e., strategic customers’ net profit is negative at the salvage sale phase. Comparing the two conditions in case 3, obviously, the optimal water resources ordering quantity under condition a is more than that under condition b, the retail price under condition a is lower than that under condition b, and the initial wholesale price and second-ordering wholesale price under condition a are the same as those under condition b. The optimal profits of the whole supply chain, local supplier, and external distributor under condition a are lower than those under condition b.

(4) Comparing all three cases, considering SCB and introducing the FPM help increase the profits of the whole supply chain, the local supplier, and the external distributor, and improve water use efficiency.

5 Conclusions

This study defined the supply chain system for the SNWD Project considering the actual project conditions, built a decentralized decision model and a centralized decision model with SCB and with the FPM, and constructed a coordination mechanism with a revenue-sharing contract. The results suggest the following: (1) Owing to the water shortage supplements and excess water sale policy provided by the FPM, the optimal ordering quantity of water resources is less than that without the FPM, and the optimal profits of the whole supply chain, local supplier, and external distributor are higher than they would be without the FPM. (2) The initial wholesale price and second-ordering wholesale price with SCB are higher than those without SCB, and the optimal profits of the whole supply chain, local supplier, and external distributor are higher than they would be without SCB. (3) There are two kinds of solutions for a centralized optimal model and a decentralized optimal model with SCB and the FPM. Comparing two kinds of solutions, we find that setting the retail price of unit water resources between the lowest and highest utilities of the strategic consumer helps all participants achievegreater profit. (4) Considering SCB and introducing the FPM help increase the optimal profits of the whole supply chain, supplier, and external distributor, and improve the efficiency of water resources usage.

Aviv, Y., and Pazgal, A. 2008. Optimal pricing of seasonal products in the presence of forward-looking consumers. Manufacturing and Service Operations Management, 10(3), 339-359. [doi:10.1287/ msom.1070.0183]

Cachon, G. P., and Swinney, R. 2009. Purchasing, pricing and quick response in the presence of strategic consumers. Management Science, 55(3), 497-511. [doi:10.1287/mnsc.1080.0948]

Cachon, G. P., and Swinney, R. 2011. The value of fast fashion: Rapid production, enhanced design, and strategic consumer behavior. Management Science, 57(4): 778-795. [doi:10.1287/mnsc.1100.1303]

Chen, Z. S., and Wang, H. M. 2010. Newsvendor optimization model for Eastern Route of South-to-North Water Diversion in China. China Population, Resources and Environment, 20(11), 42-47. (in Chinese)

Chen, Z. S., Wang, H. M., Qiu, L., and Chen, J. F. 2010. Evolutionary game and policy study on operations management of the Eastern Route of the South-to-North Water Diversion Project. Resources Science, 32(8), 1563-1569. (in Chinese)

Elmaghraby, W., Gülcü, A., and Keskinocak, P. 2008. Designing optimal preannounced markdowns in the presence of rational customers with multiunit demands. Manufacturing and Service Operations Management, 10(1), 126-148. [doi:10.1287/msom.1070.0157]

Ho, T. H., Tang, C. S., and Bell, D. R. 1998. Rational shopping behavior and the option value of variable pricing. Management Science, 44(12), 145-160. [doi:10.1287/mnsc.44.12.S145]

Hou, Y. H., Wang, H. M., and Qiu, L. 2008. Supply chain VMI coordination strategy for South-to-North Water Diversion. Industrial Technology and Economy, 27(2), 59-62 (in Chinese)

Hou, Y. H., Wang, H. M., Qiu, L., and Wang, H. 2008. SRSS strategy and model of South-to-North Water Transfer supply chain based on VMI contract. Systems Engineering, 26(5), 29-35. (in Chinese)

Hou, Y. H., Wang, H. M., Ma, S. J., and Lin, C. 2009. Minimum commitment and flexibility contracts of the supply chain for transferring southern water to the north. Chinese Journal of Management, 6(3), 299-326. (in Chinese)

Jacobson, R., and Obermiller, C. 1990. The formation of expected future prices: A reference price for forward-looking consumers. Journal of Consumer Research, 16(4), 420-432.

Krishna, A., Currim, I. S., and Shoemaker, R. W. 1991. Consumer perceptions of promotion activity. Journal of Marketing, 55(2), 4-16.

Krishna, A. 1994. The impact of dealing patterns on purchase behavior. Marketing Science, 13(4), 351-373. [doi:10.1287/mksc.13.4.351]

Liu, Q., and van Ryzin, G. J. 2008. Strategic capacity rationing to induce early purchases. Management Science, 54(6), 1115-1131. [doi:10.1287/mnsc.1070.0832]

Su, X. M. 2007. Inter-temporal pricing with strategic consumer behavior. Management Science, 53(5), 726-741. [doi:10.1287/mnsc.1060.0667]

Su, X. M., and Zhang, F. Q. 2008. Strategic consumer behavior, commitment, and supply chain performance. Management Science, 54(10), 1759-1773. [doi:10.1287/mnsc.1080.0886]

Su, X. M., and Zhang, F. Q. 2009. On the value of commitment and availability guarantees when selling to strategic consumers. Management Science, 55(5), 713-726. [doi: 10.1287/mnsc.1080.0991]

Su, X. M. 2010a. Optimal pricing with speculators and strategic consumers. Management Science, 56(1), 25-40. [doi:10.1287/mnsc.1090.1075]

Su, X. M. 2010b. Intertemporal pricing and consumer stockpiling. Operations Research, 58(4), 1133-1147. [doi:10.1287/opre.1090.0797]

Wang, H. M., Zhang, L. L., Wang, Z. Z., and Hu, Z. Y. 2004. A Summary of the feasible study on water resources allocation in east line of the project of water transferring from South to North. Journal ofEconomics of Water Resources, 22(3), 2-4. (in Chinese)

Wang, H. M., and Hu, Z. Y. 2005. Several issues on South-to-North Water Transfer Project supply chain operations management. Advances in Water Science, 16(6), 864-869. (in Chinese)

Wang, H. M., Zhang, L., and Yang, W. 2008. Pricing model of water resources supply chain for East-Route South-to-North Water Transfer Project. Journal of Hydraulic Engineering, 39(6), 758-762. (in Chinese)

Yin, R., Aviv, Y., Pazgal, A., and Tang, C. S. 2009. Optimal markdown pricing: Implications of inventory display formats in the presence of strategic customers. Management Science, 55(8), 1391-1408. [doi: 10.1287/mnsc.1090.1029]

Zhang, L., Wang, H. M., and Yang, W. 2008. A discriminatory pricing model and simulation to different markets of Eastern Route of the South-to-north Water Transfers supply chain. Systems Engineering, 26(3), 120-123. (in Chinese)

Zhang, L. L., Wang, H. M., and Wang, Z. Z. 2004. Supply chain contract of water resources allocation and scheduling of South-to-North Water Diversion Project. Journal of Economics of Water Resources, 22(4), 8-10. (in Chinese)

Zhang, L. L., Wang, H. M., and Wang, Z. Z. 2005. Multi-level cooperative decision-making model for water resources supply chain of east route of South-to-North Water Transfer Project under seasonal demand. Journal of Hohai University (Natural Sciences), 33(6), 616-619. (in Chinese)

Zhu, J. L., and Wang, H. M. 2005. Analysis of bullwhip effect in supply chain management of water resources in East-Route of South-to-North Water Transfer Project. Journal of Economics of Water Resources, 23(3), 8-11. (in Chinese)

Zhu, J. L., Wang, H. M., Tao, X. Y., and Tong, J. P. 2005. The design and the analysis on SCM structure of water resource in East-Route of South-to-North water transfer. Haihe Water Resources, 24(1), 48-51. (in Chinese)

Zhu, J. L., Tao, X. Y., and Wang, S. J. 2006. Water inventory coordination of South-to-North Water Transfer Project supply chain based on the theory of VMI. Chinese Journal of Management Science, 14(6), 98-103. (in Chinese)

Zhu, J. L. 2007. A water allocation model for supply chain in South-to-North Water Transfer Project. Systems Engineering, 25(11), 31-35. (in Chinese)

Zhu, J. L. 2008. Water resources inventory management for South-to-North Water Diversion supply chain. Yellow River, 30(2), 37-38. (in Chinese)

Zhu, J. L. 2008. The study on inventory model of SCM of water resource under asymmetric information. Journal of Industrial Engineering and Engineering Management, 22(1), 98-101. (in Chinese)

(Edited by Yan LEI)

This work was supported by the National Natural Science Foundation of China (Grants No. 50379009, 90924027 and 41101509), the National Social Science Foundation of China (Grant No. 10AJY005), and the Research Innovation Program for College Graduates of Jiangsu Province of 2009 (Grant No. CX09B_057R).

*Corresponding author (e-mail: hmwang@hhu.edu.cn)

Received May 3, 2011; accepted Oct. 28, 2011