Experimental study on modulational instability and evolution of crescent waves

Ya-long ZHOU*, Zhi-li ZOU, Kai YAN

State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology,

Dalian 116024, P. R. China

Experimental study on modulational instability and evolution of crescent waves

Ya-long ZHOU*, Zhi-li ZOU, Kai YAN

State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology,

Dalian 116024, P. R. China

A series of experiments on the instability of steep water wave trains in water with finite water depths and infinite water depths in a wide wave basin were performed. It was found that under the coupled development of modulational instability and class-II instability, the initial two-dimensional steep wave trains evolved into three-dimensional crescent waves, followed by the occurrence of disordered water surfaces, and that the wave energy transferred to sidebands in the amplitude spectrum of the water surface elevation. The results also show that water depth has a significant effect on the growth of modulational instability and the evolution of crescent waves. The larger the water depth, the more quickly the modulational instability suppresses class-II instability.

modulational instability; class-II instability; crescent wave; amplitude spectrum; wave energy transfer

1 Introduction

It is well known that there are two kinds of instabilities related to Stokes waves, i.e., class-I and class-II instabilities, classified by the even and odd numbers of waves involved in resonant waves. The growth of these two kinds of instabilities depends on the wave steepness and the relative water depth. The interaction between quartet waves falls under class-I instability, while the interaction between quintet waves falls under class-II instability (Mclean 1982a, 1982b). Modulational instability of two-dimensional waves is also called class-I instability or Benjamin and Feir instability, as it was first discovered by Benjamin and Feir (1967). Modulational instability is dominant in the evolution of waves with little and moderate initial steepness Ak (A is the wave amplitude, and k is the wave number). The modulated waves are caused by modulational instability, and the initial evolution stage is found to be characterized by exponential growth of modulational instability. At the later stage of evolution, it is found that the instability does not lead to wave train disintegration. Instead, a series of modulation-demodulation cycles appears; the modulation periodically increases and decreases.The uniform modulation-demodulation cycle is called the Fermi-Pasta-Ulam recurrence (Wu and Patton 2007; Akhmediev and Ankiewicz 2011). However, Stokes waves with a large degree of steepness (Ak > 0.25) are prone to be affected by class-II instability, and class-II instability will eventually cause initially uniform two-dimensional wave trains to evolve into three-dimensional crescent waves. These crescent-shaped wave patterns are characterized by strong three-dimensional nonlinear forms and are often observed on the sea surface under the action of wind or in wave tank experiments. Their wave heights often reach the breaking limit and thus have large impacts on marine structures. Therefore, attention needs to be paid to them in improving the design of marine structures. Additionally, from the point of view of ocean science, the three-dimensional crescent-shaped wave patterns are also very important since they modify the airflow over the sea surface and consequently affect the air-sea momentum transfer, while also changing radar scattering from the sea surface in a specific way (Annenkov and Shrira 1999). The fascinating phenomena caused by crescent-shaped wave patterns have attracted the attention of many scholars, such as Melville (1982), Su (1982), Su et al. (1982), Kusaba and Mitsuyasu (1986), Shrira et al. (1996), Collard and Caulliez (1999), and Fructus et al. (2005).

The coupled development of modulational instability and class-II instability has mostly been studied experimentally or numerically for waves with little and moderate initial steepness in deep water. Su and Green (1984, 1985) conducted experiments on the coupled interaction between modulational instability and class-II instability and concluded that for waves with initially moderate steepness (0.12 ≤ Ak≤ 0.20), the initial two-dimensional wave trains would undergo a considerable modulation on their envelope and trigger class-II instability in a certain region with a high enough degree of wave steepness. They also observed that for waves with initial wave steepness Ak≥ 0.15, the triggered class-II instability led to three-dimensional wave breaking. Stiassnie and Shemer (1987) examined the coupled development of modulational instability and class-II instability in infinitely deep water using the modified Zakahrov equation. They found that in contrast to the development of single modulational instability or class-II instability, the coupled behavior of the two classes of instabilities was non-periodic. Except for very steep waves, they observed a dominance of modulational instability over class-II instability and did not find the triggering mechanism of class-II instability. Fuhrman et al. (2004) numerically investigated the competition between the two classes of wave instabilities under various resonant interactions from their initial state up to the breaking point. The results showed that multiple instabilities can grow and contribute to the eventual wave breaking simultaneously, provided that they are of similar strength. Fructus et al. (2005) numerically investigated the interaction between modulational instability and class-II instability for relatively small initial wave steepness (Ak = 0.10, 0.13, and 0.20), and the numerical results were in agreement with the experiments of Su and Green (1985).

To the authors’ knowledge, the experimental study of the coupled development ofmodulational instability and class-II instability at finite water depths has not been reported yet. The main goal of the present experiment is to perform a study on the competition between the two classes of wave instabilities in water with finite water depths and infinite water depths. Based on the data of experiments, the effects of water depth on the crescent wave pattern, the amplitude spectrum, and the harmonic amplitudes corresponding to each frequency component of crescent waves as well as the influence of modulational instability were analyzed.

2 Experimental setup

The experiment was conducted in a wave basin in the State Key Laboratory of Coastal and Offshore Engineering at Dalian University of Technology, which was 32 m long, 24 m wide, and 1.0 m deep. The basin was equipped with a hydraulically driven piston-type wave maker at one side and a wave absorbing beach at the other side. Two parallel wave guiding walls were set up along the longitudinal direction of the basin, between which wave motions were observed. The interval between the two wave guiding walls was 23.28 m. A coordinate system with the x-axis pointing along the longitudinal direction of the basin and the y-axis lying along the still paddle was chosen. The distribution of capacitance-type wave gauges for measuring the surface elevation is shown in Fig. 1. Photographs of water surfaces were taken during the experiments to record various evolution stages of wave trains.

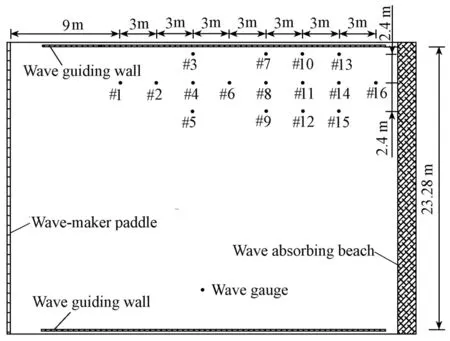
Fig. 1Experiment layout

The nonlinear evolution of gravity wave trains mainly depends on the initial wave steepness and water depth. The effects of water depth on the generation of crescent waves were examined at different water depths. Five water depths (h = 0.2 m, 0.3 m, 0.4 m, 0.5 m, and 0.6 m) and two wave periods (T = 0.7 s and 1.0 s) were used in the experiments. The corresponding relative water depth kh was from 1.37 to 4.93, covering the range from the finite water depth (kh ＜ 3.14, corresponding tohL＜ 1/2, where L is the wave length) to the infinite water depth (kh > 3.14, corresponding to hL> 1/2). Table 1 lists the related wave parameters, in which Ak is the wave steepness, larger than the critical wave steepness of Stokes waves transforming to crescent waves, and H is the wave height.

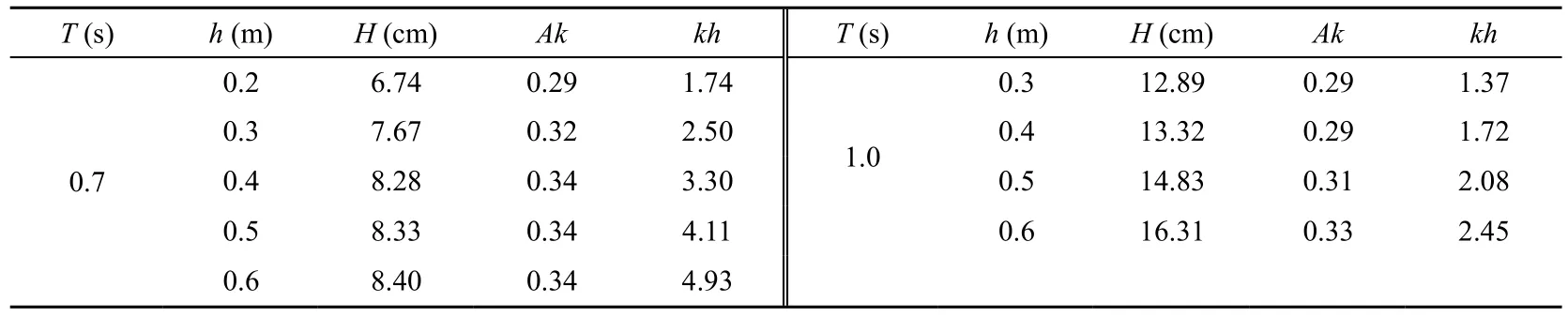
Table 1Wave parameters

3 Evolution of wave patterns

In the experiment on waves with T = 0.7 s, uniform two-dimensional Stokes waves were observed in the early stage when the instability had not developed to influence the wave pattern, as shown in Fig. 2. Then, symmetric three-dimensional crescent waves appeared clearly in the middle area of the basin because of the dominance of class-II instability. However, at the end of the basin, the crescent waves disappeared. Then, the wave pattern became rather disordered, and the modulation waves evolved. The disappearance of the crescent waves was due to the growth of modulational instability, which caused a large spatial variation of wave height, and finally caused wave breaking and led to smaller wave steepness. Thus, the conditions for triggering crescent waves were not met, and crescent waves could not develop. Therefore, the evolution of gravity waves with T = 0.7 s was influenced not only by class-II instability, but also by modulational instability. However, in the case of waves with T = 1.0 s, the crescent wave pattern was the typical L2-type (Su 1982), and this distinct three-dimensional pattern retained its form until the end of the wave basin, as can be seen in Fig. 3. The phenomenon in this case, which is different from that in the case of waves with T = 0.7 s, may have been caused by the insufficient length of the wave basin.

Fig. 2Photos illustrating effect of modulational instability on evolution of crescent waves for T= 0.7 s

Fig. 3Photos illustrating effect of modulational instability on evolution of crescent waves for T=1.0 s

4 Time series of water surface elevation and amplitude spectra

The general characteristics of wave evolution described above were further investigated by analyzing water surface elevations measured at eight wave gauges along the longitudinal direction of the wave basin. Figs. 4 and 5 show time series of the water surface elevation η from x = 9 m to x = 30 m and the corresponding amplitude spectra in the case of waves with h = 0.3 m and T = 0.7 s (finite water depth). The amplitude spectra were computed from the time series of the water surface elevation through the fast Fourier transform. The different evolution stages of waves can be distinguished by comparing the results in the figures.

Fig. 4Time series of water surface elevation at various evolution stages of waves for h = 0.3 m and T = 0.7 s

The time series of the water surface elevation at wave gauge #1 (x = 9 m, xL= 11.97) has nearly uniform wave height with very small modulation, corresponding to the evolution stage of Stokes waves. At the next wave gauge #2 (x = 12 m, xL= 15.96), the waves exhibit more amplitude modulation, and the amplitude modulation grows gradually as the waves propagate. The results at wave gauges #4 (x = 15 m, xL= 19.95), #6 (x = 18 m, xL= 23.94), and #8 (x = 21 m, xL= 27.93) correspond to the well-developed L2-type crescent waves, which show the main characteristics of crescent waves: higher crests and lower crests appear alternatively, the front slope of a crest is steeper than the rear one, and the trough in front of a higher crest is deeper than that in the rear. The amplitude spectra (Fig. 5) corresponding to these three wave gauges show a distinct peak at ωω0= 1.5 (ω is the wave frequency, and ω0is the frequency of the fundamental wave) in addition to the peaks at the fundamental frequency (ω ω0= 1) and higher frequencies (ω ω0= 2 and 3), which is a characteristic of crescent waves. At the last three wave gauges, #11 (x = 24 m, xL= 31.91), #14 (x = 27 m,xL= 35.90), and #16 (x = 30 m, xL= 39.89), the crescent waves gradually disappear. The wave train becomes disordered with significantly less steepness. The amplitude spectra for these three wave gauges clearly exhibit additional peaks at ωω0= 0.8 and 1.2, indicating that there is a wave energy transfer from the fundamental frequency to sidebands, resulting from modulational instability. We can also find that the peak at ωω0= 0.8 is obviously larger than that at ωω0= 1.2, showing that the wave energies transferred to sidebands are not symmetric: the lower sideband component grows faster than the upper sideband one. This agrees with the experimental results of Tulin and Waseda (1999), Hwung et al. (2007), and Ma et al. (2010), but does not agree with the corresponding theoretical results (Benjamin and Feir 1967), which indicates that wave energies at sidebands are symmetric about the fundamental frequency. The reason for this difference is due to the fact that the wave breaking accelerates the energy transfer to the lower sideband, but suppresses the energy transfer to the upper sideband contrary.

Fig. 5Amplitude spectra at various evolution stages of waves for h = 0.3 m and T = 0.7 s

5 Water depth effects on modulational instability and evolution of crescent waves

To show water depth effects on modulational instability and the evolution of crescent waves, the results of a representative experiment on waves with h = 0.6 m and T = 0.7 s in a deep water case are given in Figs. 6 and 7, in which the water depth is different but the wave period is the same as those in Figs. 4 and 5. By comparing the time series of the water surface elevation in two cases in Fig. 4 (h = 0.3 m) and Fig. 6 (h = 0.6 m), a distinct difference can be seen: the wave train evolves into crescent waves in Fig. 6 at wave gauge #2, which does not occur in Fig. 4. Thus, the class-II instability in deep water grows more quickly than that in shallow water.

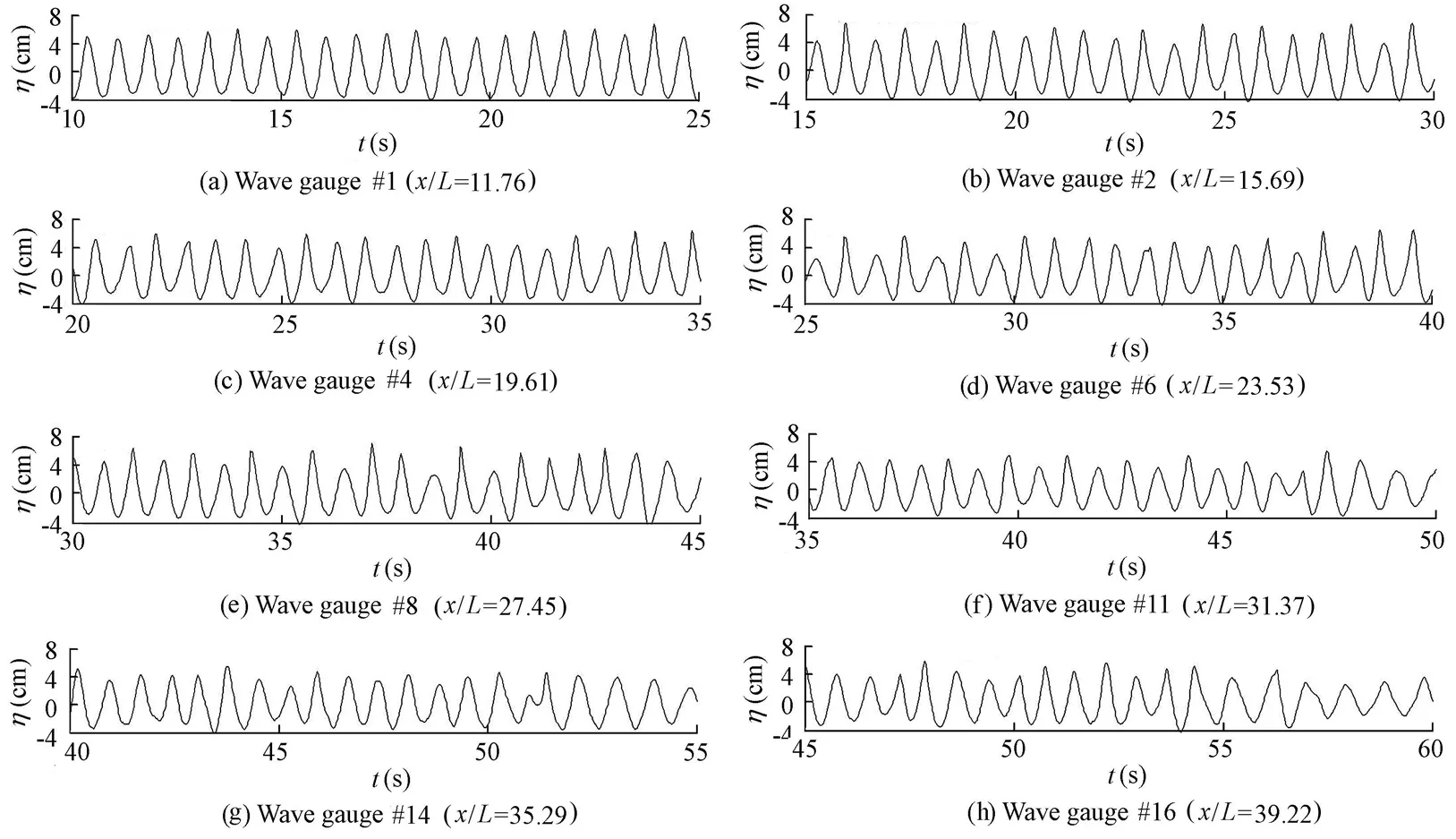
Fig. 6Time series of water surface elevation at various evolution stages of waves for h = 0.6 m and T = 0.7 s

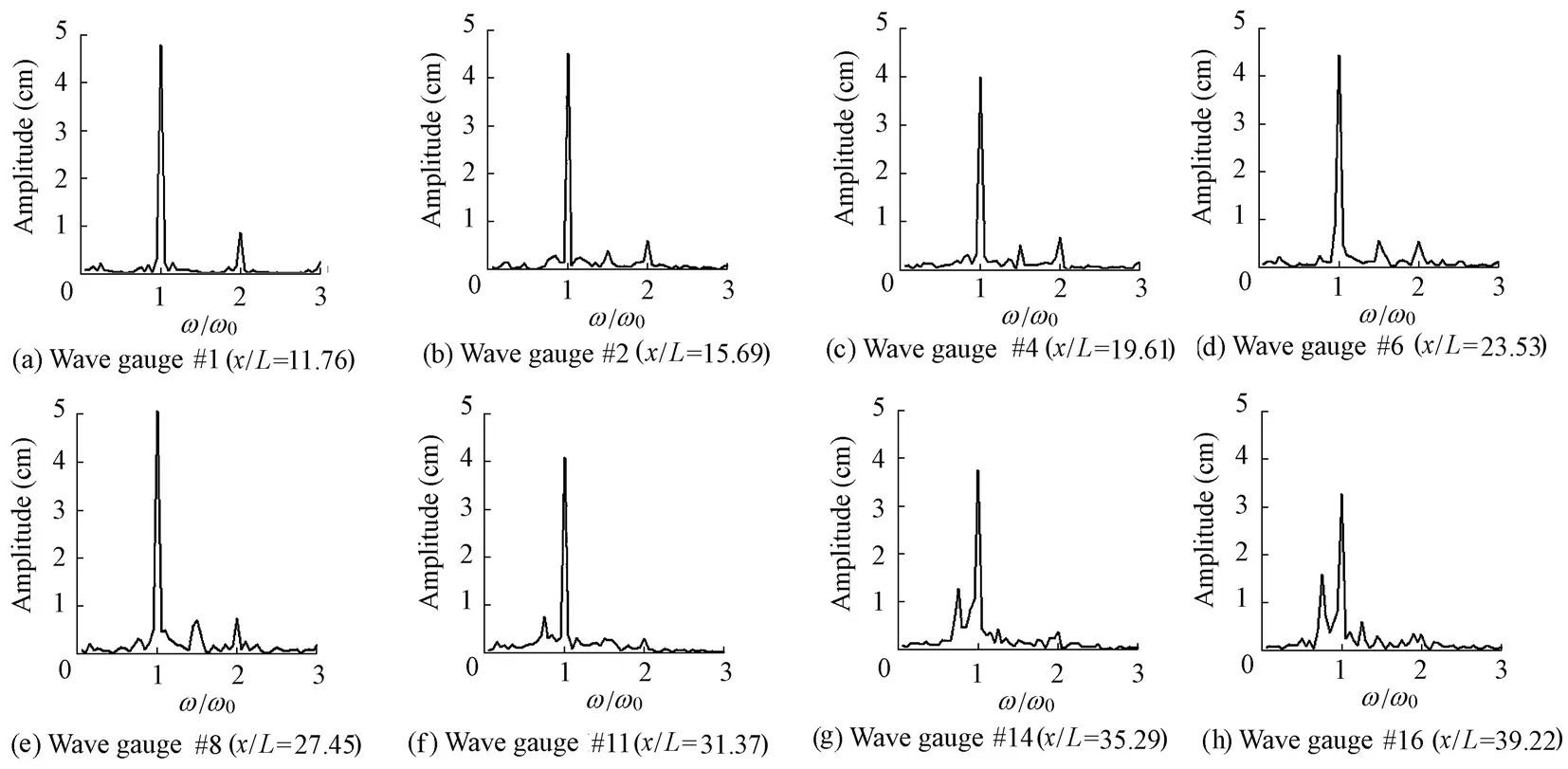
Fig. 7Amplitude spectra at various evolution stages of waves for h = 0.6 m and T = 0.7 s

Comparing the amplitude spectra in the two cases in Figs. 5 and 7, we can find that there is no significant difference between the two cases at wave gauges #1, #4, #6, and #8. Wave energy at wave gauge #1 mostly distributes at the fundamental frequency (ω ω0= 1) and higher harmonics (ω ω0= 2 and 3), which is the typical characteristic of Stokes waves. Wave energy at wave gauges #4, #6, and #8 shows an additional peak at ωω0= 1.5, which is the typical characteristic of crescent waves. This shows that water depth has little effect on the amplitude-spectrum features of Stokes waves and crescent waves. However, the amplitude spectra for waves with two different water depths show an obvious difference at wave gauges #11, #14, and #16. There is a relatively large wave energy transfer toward the lower sideband for h = 0.6 m, but for h = 0.3 m little wave energy distributes at lower and upper sidebands(ωω0= 0.8 and 1.2). The result of h = 0.2 m is similar to that of h = 0.3 m, and the results of h = 0.4 m and 0.5 m are between those of h = 0.3 m and 0.6 m. Thus, the larger the water depth is, the more remarkable the energy transfer is. We can conclude that modulational instability has a larger growth rate in deep water. A larger peak occurring at ω ω0= 0.8, as compared with that at ωω0= 1.2, also shows that the evolutions of sidebands in amplitude spectra are not symmetric, with lower sideband components growing faster than upper sideband ones.

The distances from the wave-maker paddle to the emerging and disappearing points of crescent waves were measured in the experiment: 15 m (xL= 20.83) and 28 m (xL= 38.89), respectively, for the shallowest water (h = 0.2 m), and 12 m (xL= 15.69) and 25 m (xL= 32.68), respectively, for the deepest water (h = 0.6 m). The results of h = 0.3 m, 0.4 m, and 0.5 m varied between those of h = 0.2 m and 0.6 m. The values of the distance from the wave-maker paddle to the emerging points of crescent waves were 14 m, 13 m, and 13 m, respectively, for h = 0.3 m, 0.4 m, and 0.5 m, and the values of the distance from the wave-maker paddle to the disappearing points of crescent waves were 27 m, 26 m, and 25 m, respectively, for the three different water depths mentioned above. The results demonstrate that the deeper the water is, the faster the growth of modulational instability and class-II instability, and also the more quickly the modulational instability suppresses class-II instability.

6 Conclusions

The effect of modulational instability on the evolution of crescent waves was experimentally investigated at different water depths. It was found that modulational instability affected the evolution of crescent waves by changing the uniform wave height into spatially varying ones which led to the evolution of modulation waves. It was also found that two peaks occurring at the sidebands of ωω0= 0.8 and 1.2 in amplitude spectra of the water surface elevation caused by the growth of modulational instability were asymmetric about the fundamental frequency (ω ω0= 1.0), and that the peak at the lower sideband was higher than that at the upper sideband. This result agrees with experimental results of Tulin and Waseda (1999), Chiang and Hwung (2007), Hwung et al. (2007), and Ma et al. (2010). The emergence of crescent waves is due to the growth of class-II instability and their disappearance is due to the overgrowth of modulational instability. The experimental results show that water depth has a remarkable effect on the growth of modulational instability and the evolution of crescent waves: the larger the water depth is, the more quickly the modulational instability suppresses class-II instability.

Akhmediev, N., and Ankiewicz, A. 2011. Modulation instability, Fermi-Pasta-Ulam recurrence, rogue waves, nonlinear phase shift, and exact solutions of the Ablowitz-Ladik equation. Physical Review E, 83(4), 46603-46613. [doi:10.1103/PhysRevE.83.046603]

Annenkov, S. Y., and Shrira, V. I. 2001. Numerical modelling of water-wave evolution based on the Zakharov equation. Journal of Fluid Mechanics, 449, 341-371. [doi:10.1017/S0022112001006139]

Benjamin, T. B., and Feir, J. E. 1967. The disintegration of wave trains on deep water, Part 1: Theory. Journal of Fluid Mechanics, 27(3), 417-430. [doi:10.1017/S002211206700045X]

Chiang, W. S., and Hwung, H. H. 2007. Steepness effect on modulation instability of the nonlinear wave train. Physics of Fluids, 19(1), 1-13. [doi:10.1063/1.2433941]

Collard, F., and Caulliez, G. 1999. Oscillating crescent-shaped water wave patterns. Physics of Fluids, 11(11), 3195-3197. [doi:10.1063/1.870215]

Fructus, D., Clamond, D., Grue, J., and Kristiansen, Ø. 2005. An efficient model for three-dimensional surface waves simulations, Part I: Free space problem. Journal of Computational Physics, 205(2), 665-685. [doi:10.1016/j.jcp.2004.11.027]

Fuhrman, D. R., Madsen, P. A., and Bingham, H. B. 2004. A numerical study of crescent waves. Journal of Fluid Mechanics, 513, 309-341. [doi:10.1017/S0022112004000060]

Hwung, H. H., Chiang, W. S., and Hsiao, S. C. 2007. Observations on the evolution of wave modulation. Proceedings of the Royal Society of London, Series A, Mathematical, Physical and Engineering Sciences, 463(2077), 85-112. [doi:10.1098/rspa.2006.1759]

Kusuba, T., and Mitsuyasu, M. 1986. Nonlinear instability and evolution of steep water waves under wind action. Reports of the Research Institute for Applied Mechanics, 33, 33-64.

Ma, Y., Dong, G., Perlin, M., Ma, X., Wang, G., and Xu, J. 2010. Laboratory observations of wave evolution, modulation and blocking due to spatially varying opposing currents. Journal of Fluid Mechanics, 661, 108-129. [doi:10.1017/S0022112010002880]

McLean, J. W. 1982a. Instabilities of finite-amplitude water waves. Journal of Fluid Mechanics, 114, 315-330. [doi:10.1017/S0022112082000172]

McLean, J. W. 1982b. Instabilities of finite-amplitude gravity waves on water of finite depth. Journal of Fluid Mechanics, 114, 331-341. [doi:10.1017/S0022112082000184]

Melville, W. K. 1982. The instability and breaking of deep-water waves. Journal of Fluid Mechanics, 115, 165-185. [doi:10.1017/S0022112082000706]

Shrira, V. I., Badulin, S. I., and Kharif, C. 1996. A model of water wave ‘horse-shoe’ patterns. Journal of Fluid Mechanics, 318, 375-405. [doi:10.1017/S0022112096007161]

Stiassnie, M., and Shemer, L. 1987. Energy computations for evolution of class I and II instabilities of Stokes waves. Journal of Fluid Mechanics, 174, 299-312. [doi:10.1017/S0022112087000132]

Su, M. Y. 1982. Three dimensional deep-water waves, Part 1: Experimental measurement of skew and symmetric wave patterns. Journal of Fluid Mechanics, 124, 73-108. [doi:10.1017/ S0022112082002419]

Su, M. Y., Bergin, M., Marler, P., and Myrick, R. 1982. Experiments on nonlinear instabilities and evolution of steep gravity-wave trains. Journal of Fluid Mechanics, 124, 45-72. [doi:10.1017/ S0022112082002407]

Su, M. Y., and Green, A. W. 1984. Coupled two- and three-dimensional instabilities of surface gravity waves. Physics of Fluids, 27(11), 2595-2597. [doi:10.1063/1.864556]

Su, M. Y., and Green, A. W. 1985. Wave breaking and nonlinear instability coupling. Toba, Y., and Mitsuyasu, H., eds., The ocean Surface: Wave breaking, Turbulent Mixing and Radio Probing. Dordrecht: D. Reidel Publishing Company.

Tulin, M. P., and Waseda, T. 1999. Laboratory observations of wave group evolution, including breaking effects. Journal of Fluid Mechanics, 378, 197-232. [doi:10.1017/S0022112098003255]

Wu, M., and Patton, C. E. 2007. Experimental observation of Fermi-Pasta-Ulam recurrence in a nonlinear feedback ring system. Physical Review Letters, 98(4), 47202-47205. [doi:10.1103/PhysRevLett.98. 047202]

(Edited by Ye SHI)

This work was supported by the National Natural Science Foundation of China (Grant No. 51079024) and the National Foundation for Creative Research Groups (Grant No. 50921001).

*Corresponding author (e-mail: ylzhou@mail.dlut.edu.cn)

Received Oct. 18, 2011; accepted Dec. 26, 2011