波导传播特性的二次FEM方法分析研究

潘建伟

（武威职业学院，甘肃 武威 733000）

0 引言

本征值问题是微波技术中最基本的问题之一。对于亥姆霍兹方程的求解,除少数规则波导可用分离变量法求得其解析解外,绝大多数都采用近似方法求解。有限元法剖分灵活,边界条件易处理,便于处理复杂媒质,而且程序通用性强,已是数值计算中应用最广泛的一种方法。但目前广泛用的是三角形上的三节点线性插值函数的简单插值方法,只有剖分密度极大时才能满足某些工程的需要，但是消耗了大量的计算机内存，于是高次插值函数应运而生，它可用较少的单元来获得较高的精度。由于对背脊波导的数值计算至尽还未有报道，特别是常用于介质加载移相器的波导，因为它的加载结构，使得差相移增大，插入损耗降低，优值大大提高，体积减小，重量减轻，目前已在S、C、X波段广泛应用，功率承受能力也得到了一定程度的提高。因此文中在综合介绍二次有限元基本原理的基础上，用二次FEM实例计算了矩形波导，背脊波导。

1 二次单元的有限元分析

1.1 二次三角形单元及插值函数

一个二次三角形单元有6个节点，3个顶点和3个边中间点各一个，如图1所示。设三角形单元内某点的场是6个节点上场的二次插值：

在6个节点上强加式（1），即可确定上式中的6个系数 ae, be, ce, de, ee, fe，将它们代回到式（1），得到：

假设节点的编码如图1所示，则上式中的插值函数为：

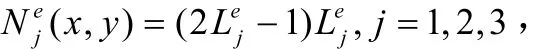
二阶三角形单元的单元矩阵则是66×的矩阵，其元素如下：

列向量eb的元素为：

如果在每个单元内的系数xα，yα，β和源f均为常数，并分别用表示，那么，应用式，可以解析求式（6）和式（7）中的积分，得到：

图1 二次元上节点配置

1.2 有限元方程

波在金属波导中传播时，场的纵向分量φ(Ez或Hz)应满足Helmholtz方程[5]即：

等价泛函为：

根据1.1节中的基本式，其中单元et产生的局部Ket、Bet系数可通过以下两个积分进行计算：

上述的积分在自然坐标下可以直接解出,无需使用数值积分法。局部系数等于：

式中：

1.3 边界条件处理

式中，M表示在金属边界l上的节点数,这些节点的编号分别为 h1,h2,…,hM。式(12)结合式(18)把变分问题式(11)最终离散化为广义代数本征值问题：

求解式(19)即可获得本征值和相应的本征函数。由于这两类波导的基模都是 TE模，在实际工作中，一般都应用在基模，所以在这里只讨论了TE的计算。

2 计算实例

背脊波导如图2所示。

图2 背脊波导

2.1 截止波长

首先为了验证程序的正确性，计算了矩形波导（23 cm×10 cm）的特征值。一次有限元划分时，单元数为96，节点数为63，二次有限元划分是单元数为24，节点数也为63。计算结果见表1所示。

由表1的数据表明，二次FEM方法较传统的有限元方法，在相同的节点数下，单元数少，而且具有较高的精度。为了验证二次有限元法计算背脊波导程序的正确性，表2列出了b1/a1=0.45时双脊背脊波导的截止波长，根据文献[6]，表明该方法具有较高的精度。

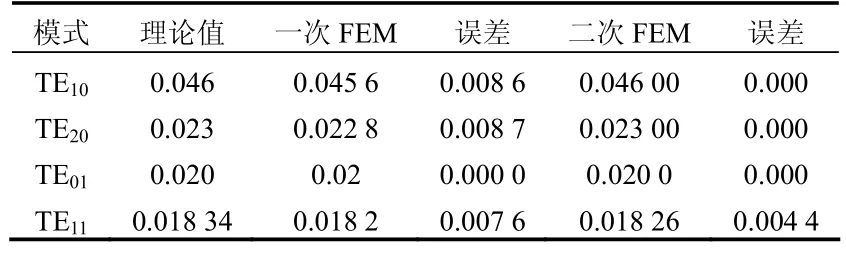
表1 矩形波导的特征值

表2 b1/a1=0.45时双脊背脊波导的截止波长

将表3与表2经过比较，发现单脊背脊波导的截止波长与双脊背脊波导的截止波长几乎相等。从而也证实了文献[6]的理论分析。

表3 b1/a1=0.45时单脊背脊波导截止波长

b2/a1=0.45时，b2/b1，a2/a1，取不同的归一化尺寸的λc/a1曲线如图3所示。

2.2 单模带宽

单模带宽定义为主模截止波长与邻近高次模波长的比值，根据特征值进行求解单模带宽，如图 4和图5所示。

2.3 场结构

当b2/b1=0.3,a2/a1=0.3时，双脊背脊波导主模的磁场分布如图6所示；当b2/b1=0.5,a2/a1=0.3时，单脊背脊波导主模的磁场分布如图7所示。

2.4 计算结果分析

文中提出用二次 FEM 方法计算波导本征值问题,为波导本征值问题提供一种新的、具有较高计算精度的新型算法。

用二次 FEM 方法计算波导本征值问题,尤其是计算 TE波，不用考虑边界条件，又能用统一的格式计算各种形状的波导本征值问题。

用二次 FEM 方法计算波导本征值问题,编程简单,计算量小,程序通用性强,一般微机就能计算实际工程问题，所用计算机内存小，适合大尺寸的问题。

从图4看出，在双脊背脊波导中，随着a2/a1从0.1逐渐增大到0.9，b2/b1=0.1～0.3时，单模带宽在a2/a1=0.3时最小，然后又逐渐增大，单模带宽在a2/a1=0.9时达到最大，单模带宽在b2/b1=0.1，0.2时具有最大值2。在b2/b1=0.4～0.9，a2/a1=0.9时，单模带宽具有相同的值1.834 0。在b2/b1=0.4～0.7时，单模带宽在a2/a1=0.4时最小，然后随着a2/a1逐渐增大而增大。当b2/b1=0.8，0.9，单模带宽在a2/a1=0.5时达到最小值。

从图5看出，在单脊背脊波导中，随着a2/a1从0.1逐渐增大到0.4单模带宽逐渐减小，然后有逐渐增大，单模带宽在a2/a1=0.3时达到最小。a2/a1最大只能取到0.4。

图4 双脊背脊波导单模带宽

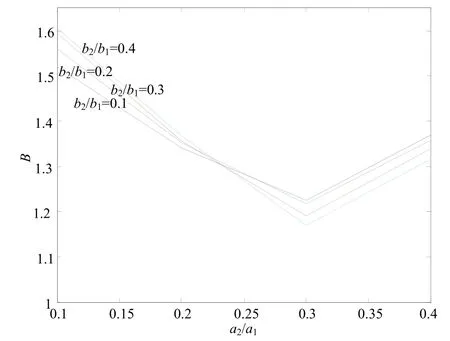
图5 单脊背脊波导单模带宽

图6 b2/b1=0.3,a2/a1=0.3时，双脊背脊波导主模的磁场分布

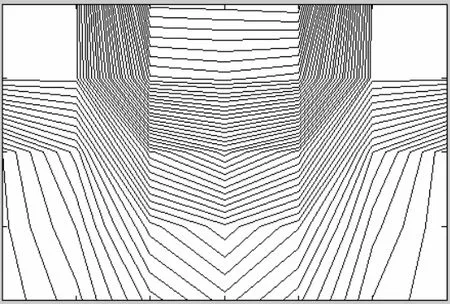
图7 b2/b1=0.5,a2/a1=0.3时，单脊背脊波导主模的磁场分布

3 结语

背脊波导主模截止波长可以通过改变脊宽而改变，以前的文献只给出了理论分析，而文中用二次FEM方法分析了波导，编制的程序验证了理论分析的正确性，而且在理论分析的基础上计算了波导的截止波长和单模带宽，分析了随着脊位置的变化截止波长和单模带宽的变化规律，为背脊波导的设计提供了理论数据。由于程序和方法的局限性，文中还不能计算出背脊波导的阻抗，希望在以后的研究中能进一步解决这个问题。

[1] 盛剑霓.工程电磁场数值分析[M].西安:西安交通大学出版社,1991:477-482.

[2] SILVESTER P. A General High-Order Finite-Element Waveguide Analysis Program[J].IEEE Trans.on MTT.,1969,17(04):204-210.

[3] 姚斌,郑勤红,帅春江.用FDTD法计算部分介质填充波导的截止频率[J].云南师范大学学报:自然科学版,2006,26(04):52-55.

[4] 倪光正,杨仕友,钱秀英.工程电磁场数值计算[M]. 北京:机械工业出社,2004:123-124,166.

[5] 曹世昌.电磁场的数值计算和微波的计算机辅助设计[M].北京:电子工业出版社,1989:98-121.

[6] 黄彩华. 矩形变形脊波导主模截止波长和特性阻抗计算[J]. 雷达与对抗,1997(03):255-258.

[7] COHN S B. Properties of Ridge Waveguide[J]. Proc.IRE,1974,35(08):783-788.

[8] HOPFER S. The Design of Ridged Waveguides[J]. IEEE Transactions on Microwave Theory and Techniques,1996,44(05):20-29.

[9] 刘勇,周新力,裴瑞杰.基于抛物方程的海上电波传播研究[J].通信技术,2012,45(01):4-6.

[10] 曹琼琼,单志勇.一种基于微带槽天线的带阻性 UWB天线的研究[J].通信技术,2012,45(02):45-48.